Diferencia entre revisiones de «Problemas de electrostática en el vacío (GIOI)»
| Línea 29: | Línea 29: | ||
[[Cuatro cargas en dos varillas|Solución]] | [[Cuatro cargas en dos varillas|Solución]] | ||
==Fuerzas y momentos sobre un par de cargas== | |||
{{nivel|2}} Dos cargas <math>q_1=+q</math> y <math>q_2=-q</math> se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico | |||
<center><math>\vec{E}=Ay\vec{\imath}+Bx^2 \vec{\jmath}</math></center> | |||
* Si los extremos de la varilla se encuentran en <math>\vec{r}_1=b\vec{\imath}</math> y <math>\vec{r}_2=-b\vec{\imath}</math>, ¿cuál es el efecto del campo sobre el sistema? | |||
* Si los extremos de la varilla se encuentran en <math>\vec{r}_1=b\vec{\jmath}</math> y <math>\vec{r}_2=-b\vec{\jmath}</math>, ¿cuál es el efecto del campo sobre el sistema? | |||
[[Fuerzas y momentos sobre un par de cargas|Solución]] | |||
Revisión del 16:08 10 abr 2024
Carga total de una distribución
Calcule la carga total de las siguientes distribuciones de carga:
 N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en .
N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en . Un anillo circular de radio b con una densidad lineal de carga uniforme .
Un anillo circular de radio b con una densidad lineal de carga uniforme . Un anillo circular de radio b con centro el origen y situado en el plano XY, con una densidad lineal de carga , siendo θ el ángulo del vector de posición con el eje OX.
Un anillo circular de radio b con centro el origen y situado en el plano XY, con una densidad lineal de carga , siendo θ el ángulo del vector de posición con el eje OX. Una superficie esférica de radio a con una densidad de carga uniforme , rodeada por una superficie esférica concéntrica de radio b con densidad de carga .
Una superficie esférica de radio a con una densidad de carga uniforme , rodeada por una superficie esférica concéntrica de radio b con densidad de carga . Una esfera maciza de radio b con densidad de carga uniforme .
Una esfera maciza de radio b con densidad de carga uniforme . Una esfera maciza de radio con una densidad de carga dependiente de la distancia al centro como ().
Una esfera maciza de radio con una densidad de carga dependiente de la distancia al centro como ().
Fuerza entre cargas en un triángulo
Tres cargas puntuales iguales +q se hallan en los vértices de un triángulo equilátero de lado b. Calcule la fuerza eléctrica sobre cada una de ellas.
Suponga que se cambia una de las cargas +q por una carga −q. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas?
Si se cambia una segunda carga +q por otra carga –q, ¿cuánto pasa a ser la fuerza sobre cada una?
Por último, si se sustituye la última carga +q por otra –q, ¿cuál es ahora la fuerza?
Cuatro cargas en dos varillas
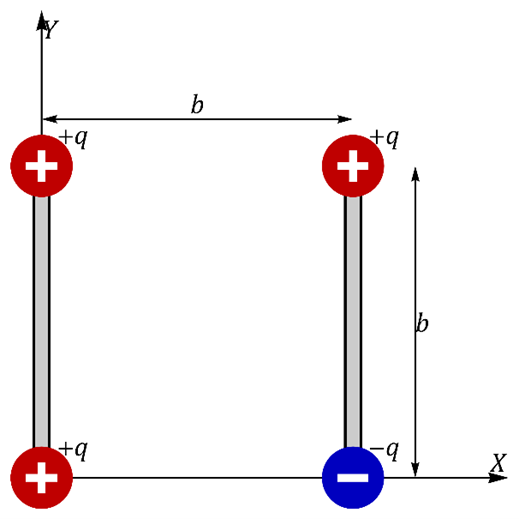
![]() Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +q, unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±q. Las cuatro cargas forman un cuadrado de lado b.
Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +q, unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±q. Las cuatro cargas forman un cuadrado de lado b.
Para cada varilla, calcule la fuerza resultante y el momento resultante respecto a su centro de masas (centro de cada varilla).
Fuerzas y momentos sobre un par de cargas
![]() Dos cargas y se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico
Dos cargas y se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico
- Si los extremos de la varilla se encuentran en y , ¿cuál es el efecto del campo sobre el sistema?
- Si los extremos de la varilla se encuentran en y , ¿cuál es el efecto del campo sobre el sistema?















