Problemas de cinemática del sólido rígido (GIOI)

Caso de campo de velocidades de un sólido

El campo de velocidades instantáneo de un sólido rígido tiene la expresión, en el sistema internacional

${\vec {v}}(x,y,z)=\left((7.2+0.8y+1.6z){\vec {\imath }}+(3.6-0.8x+1.6z){\vec {\jmath }}-(7.2+1.6x+1.6y){\vec {k}}\right){\frac {\mathrm {m} }{\mathrm {s} }}$

1. Determine la velocidad angular, ${\vec {\omega }}$, y la velocidad del origen de coordenadas, ${\vec {v}}_{0}$.
2. Halle la velocidad del punto ${\vec {r}}_{1}=(-5.0{\vec {\imath }}-6.0{\vec {k}})\,\mathrm {m}$.
3. ¿Qué tipo de movimiento describe el sólido en este instante?
4. Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o eje instantáneo de rotación, en su caso).

Solución

Movimiento conocidas las velocidades de tres puntos

Una esfera centrada en el origen de coordenadas se mueve de forma que, en un instante dado la velocidad del punto $A(1,0,0)$ es ${\vec {v}}_{A}=3{\vec {\imath }}+a{\vec {\jmath }}+{\vec {k}}$, la de $B(0,1,0)$ es ${\vec {v}}_{B}={\vec {\imath }}-6{\vec {\jmath }}+b{\vec {k}}$ y la de $C(0,0,1)$ es ${\vec {v}}_{C}=c{\vec {\imath }}-5{\vec {\jmath }}+3{\vec {k}}$ (todo en las unidades fundamentales del SI). Para este instante, determine, en el orden que crea más oportuno:

1. Los valores de las constantes a, b y c.
2. La velocidad del origen de coordenadas,
3. La velocidad angular del sólido.
4. La velocidad de deslizamiento.
5. El tipo de movimiento que está realizando el sólido.
6. La posición de dos puntos del eje instantáneo de rotación y mínimo deslizamiento (o eje instantáneo de rotación, en su caso).
7. Si este movimiento es permanente, es decir, la velocidad angular y la velocidad de O en todo momento tienen los valores calculados en (2) y (3), ¿tiene aceleración el punto O? ¿Por qué? Si la respuesta es sí, ¿cuánto vale?

Solución

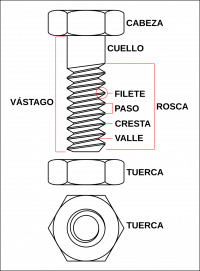
Rapidez de los puntos de un tornillo

Un tornillo de radio 2 mm y paso de rosca 1 mm avanza impulsado por un destornillador de forma que su punta se mueve a 2 mm/s. Determine la rapidez de los puntos del filete del tornillo.

Solución

Tres casos de movimiento de un sólido

Un sólido se mueve de forma que en un instante dado el origen O tiene una velocidad ${\vec {v}}_{O}$ y su velocidad angular es ${\vec {\omega }}$. Para los casos siguientes:

${\vec {v}}_{O}$	${\vec {\omega }}$
${\vec {\imath }}-2{\vec {\jmath }}+2{\vec {k}}$	${\vec {0}}$
${\vec {\imath }}-2{\vec {\jmath }}+2{\vec {k}}$	$2{\vec {\imath }}-2{\vec {\jmath }}+{\vec {k}}$
${\vec {\imath }}-2{\vec {\jmath }}+2{\vec {k}}$	$2{\vec {\imath }}+2{\vec {\jmath }}+{\vec {k}}$

Determine:

1. Si el estado es de reposo, traslación, rotación o movimiento helicoidal.
2. La velocidad instantánea del punto $A(1,0,0)$ y del $P(1,1,1)$.
3. La velocidad de deslizamiento.
4. La posición, en su caso, del Eje Instantáneo de Rotación y Mínimo Deslizamiento dando un punto por el que pasa y un vector en la dirección del eje.

Solución

Diferentes movimientos de una esfera

Considérese una esfera de masa $M$ y radio $R$ que se mueve sobre la superficie horizontal $z=0$. Consideramos un instante en el que la esfera toca el suelo justo en el origen de coordenadas, O, y tal que en ese momento la velocidad de dicho punto de contacto con el suelo es nula

${\vec {v}}_{O}={\vec {0}}$

Para este mismo instante la velocidad de los puntos ${\vec {r}}_{A}=-R{\vec {\imath }}+R{\vec {k}}$ y ${\vec {r}}_{B}=+R{\vec {\imath }}+R{\vec {k}}$ situados en un diámetro horizontal valen respectivamente

${\vec {v}}_{A}=v_{A}{\vec {\jmath }}\qquad {\vec {v}}_{B}=v_{B}{\vec {\jmath }}$

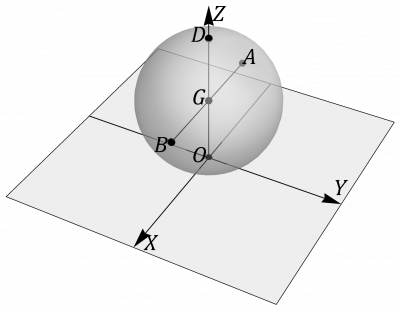
Para los tres casos siguientes:

• $v_{A}=+v_{B}$
• $v_{A}=0$
• $v_{A}=-v_{B}$

1. Indique justificadamente el tipo de movimiento instantáneo que realiza la esfera (traslación, rotación, helicoidal,…)
2. Calcule la velocidad angular del sólido.
3. Halle la velocidad angular de pivotamiento y la de rodadura de la esfera.
4. Dé la ecuación del eje instantáneo de rotación y mínimo deslizamiento (o de rotación, en su caso).
5. Calcule la velocidad lineal del centro C de la esfera y la del punto D situado en el extremo superior de la esfera.

Solución

Movimiento de un disco dados dos puntos

Un disco de radio R y masa m rueda y desliza sobre el plano horizontal $y=0$ de forma que la velocidad del punto de contacto con el suelo, A, y del diametralmente opuesto, B, son de la forma

${\vec {v}}_{A}=v_{A}{\vec {\imath }}\qquad \qquad {\vec {v}}_{B}=v_{B}{\vec {\imath }}$

siendo $v_{A}$ y $v_{B}$ constantes.

1. Calcule la velocidad angular del disco respecto al suelo.
2. Halle la velocidad del centro del disco, G, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
3. Determine la posición del centro instantáneo de rotación.
4. Halle la aceleración instantánea de A, B, D, E y G.
5. Indique a qué se reducen los resultados anteriores en los casos particulares siguientes:
   1. $v_{A}=-v_{B}$.
   2. $v_{A}=0$.
   3. $v_{A}=v_{B}$.

Solución

Barra que desliza por pared y suelo

Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una distancia de 60 cm de la esquina y se mueve con velocidad de 12 cm/s alejándose de la esquina

1. ¿Con qué velocidad se mueve el punto B, extremo superior de la barra?
2. Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OY, ¿dónde se encuentra el C.I.R. de la barra en el instante anteriormente descrito?
3. Si en el mismo instante, la aceleración del punto A es ${\vec {a}}_{A}=21.25\,\mathrm {cm} /\mathrm {s} ^{2}{\vec {\imath }}$, ¿cuál es la aceleración de B?

Solución

Movimiento de un sistema biela-manivela

Un sistema biela-manivela está formado por: una barra fija (el eje “1”); una barra (la manivela “0”) de longitud $b$, articulada en el punto O del eje y que forma un ángulo $\theta (t)$ con él; y una segunda barra (la biela “2”), también de longitud $b$, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje.

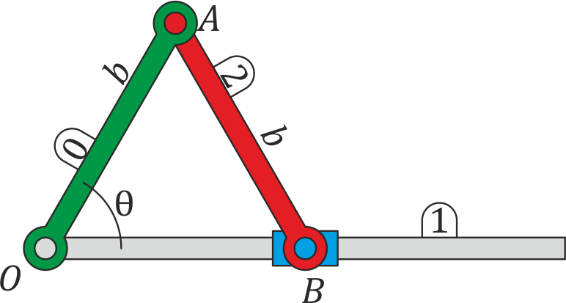
1. Halle las velocidades de los puntos A y B de la biela.
2. Determine la velocidad angular de la biela respecto al eje.
3. Localice el centro instantáneo de rotación (CIR) de la biela respecto al eje.
4. Suponga el caso $b=50\,\mathrm {cm}$ y que en un instante dado $\mathrm {tg} (\theta )=0.75$ siendo ${\dot {\theta }}=-2.00\,\mathrm {rad} /\mathrm {s}$. Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.

Solución