Segunda Convocatoria 2023/24 (G.I.C.)

Juego con bola y caja

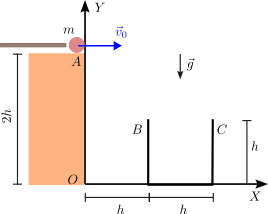
La figura ilustra un juego muy simple. Se trata de golpear una bola de masa $m$ con un taco en reposo en $t=0$, de modo que, justo después del impacto, se mueve con velocidad ${\vec {v}}_{0}$ horizontal, como se muestra en la figura. Después del impacto, la bola se mueve en caída libre, con rozamiento del aire despreciable. Se gana en el juego si se consigue que la bola entre en la caja $BC$ de la figura. En lo que sigue, modelaremos la bola como una partícula puntual de masa $m$.

1. Escribe las expresiones de los vectores ${\vec {v}}(t)$ y ${\vec {r}}(t)$ que describen la posición de la bola en cada instante de tiempo.
2. Encuentra el instante de tiempo, $t_{h}$, para el cual la distancia de la bola al suelo (el eje OX) es $h$.
3. Encuentra que condiciones debe cumplir $|{\vec {v}}_{0}|$ para ganar el juego.
4. Si la velocidad de salida de la partícula es $v_{0}=1.0\,\mathrm {m/s}$, y su masa es $m=1.00\,\mathrm {kg}$, ¿cuál es el impulso mecánico impartido por el taco a la partícula?

Masas en plano inclinado con cuerda tirando

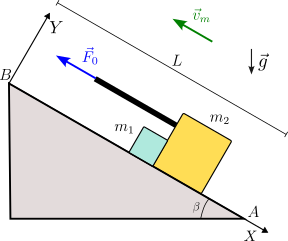
Dos masas, $m_{1}$ y $m_{2}$, deslizan sobre un plano inclinado un ángulo $\beta$ con la horizontal. El contacto entre las masas y el plano inclinado es liso. Una cuerda tensa ejerce una fuerza ${\vec {F}}_{0}=-F_{0}\,{\vec {\imath }}$ ($F_{0}>0$) sobre la masa 2, como se indica en la figura. Las masas se desplazan siempre juntas hacia arriba, con velocidad constante ${\vec {v}}_{m}=-5v_{0}\,{\vec {\imath }}$ ($v_{0}>0$). Las masas son $m_{1}=5m_{0}$, $m_{2}=10m_{0}$. Las dos masas se tratan como partículas puntuales. La longitud de la rampa del plano inclinado es $L=5L_{0}$. El ángulo $\beta$ verifica

$\mathrm {sen} \,\beta =4/5,\qquad \cos \beta =3/5.$

1. Dibuja el diagrama de fuerzas para la masas. Hazlo por separado para cada una de ellas.
2. Calcula el valor de $F_{0}$ y de la fuerza entre las masas.
3. Si en el instante inicial las dos masas estaban en el punto $A$, ¿cuál es la variación de su energía mecánica cuando llegan al punto $B$?
4. Si $L_{0}=1.00\,\mathrm {m}$, $F_{0}=100\,\mathrm {N}$, y $v_{0}=5.00\,\mathrm {m/s}$, ¿cuanto vale la potencia que ${\vec {F}}_{0}$ transmite a las masas? ¿Y el trabajo realizado por ${\vec {F}}_{0}$ entre los puntos $A$ y $B$?