Diferencia entre revisiones de «Problemas de corriente eléctrica (GIOI)»
Secciones
(Página creada con «==Cable bimetálico== Entre los distintos tipos de cable empleados en la industria, se encuentra el de ''acero revestido de cobre''. Está formado por un núcleo de acero de radio <math>a</math> (suponga <math>a=2\,\mathrm{mm}</math>), rodeado por una capa de cobre, de radio exterior <math>b</math> (sea <math>b= 3\,\mathrm{mm}</math>). # Calcule la resistencia de un cable de esta clase de longitud <math>h=10\,\mathrm{km}</math>. # Determine la intensidad de corrient…») |
|||
| (No se muestran 33 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
==Densidad de corriente radial== | |||
En una determinada región del espacio alrededor del origen de coordenadas existe una densidad de corriente dependiente de la distancia al origen como | |||
<center><math>\vec{J}(r) = A r (b-r)\vec{u}_r</math></center> | |||
con ''A'' y ''b'' dos constantes positivas, ''r'' la distancia al origen de coordenadas y <math>\vec{u}_r</math> el vector unitario radial hacia afuera. | |||
# ¿Cuánto vale la derivada respecto al tiempo de la carga contenida en una esfera de radio ''b''/2 con centro el origen? ¿Aumenta o disminuye? | |||
# ¿Y si la esfera tiene radio ''b''? | |||
# ¿Y si tiene radio 2''b''? | |||
[[Densidad de corriente radial|Solución]] | |||
==Cable bimetálico== | ==Cable bimetálico== | ||
Entre los distintos tipos de cable empleados en la industria, se encuentra el de ''acero revestido de cobre''. Está formado por un núcleo de acero de radio <math>a</math> (suponga <math>a=2\,\mathrm{mm}</math>), rodeado por una capa de cobre, de radio exterior <math>b</math> (sea <math>b= 3\,\mathrm{mm}</math>). | Entre los distintos tipos de cable empleados en la industria, se encuentra el de ''acero revestido de cobre''. Está formado por un núcleo de acero de radio <math>a</math> (suponga <math>a=2\,\mathrm{mm}</math>), rodeado por una capa de cobre, de radio exterior <math>b</math> (sea <math>b= 3\,\mathrm{mm}</math>). | ||
| Línea 28: | Línea 40: | ||
==Conexión de tres bombillas== | ==Conexión de tres bombillas== | ||
Supongamos que tenemos tres bombillas iguales (simbolizadas por ⊗) de potencia nominal 10W a | Supongamos que tenemos tres bombillas iguales (simbolizadas por ⊗) de potencia nominal 10W a 240V que se conectan según el esquema siguiente. La fuente es una de continua a 240V. | ||
<center>[[Archivo:tres-bombillas.png | <center>[[Archivo:tres-bombillas.png]]</center> | ||
# ¿Cuánta potencia consume cada bombilla? ¿Cuál da más luz? ¿Qué potencia se consume en el circuito completo? | |||
# Si ahora se abre el interruptor A, ¿cómo cambia la potencia consumida por cada bombilla? ¿Y la potencia total consumida? | |||
[[Conexión de tres bombillas|Solución]] | [[Conexión de tres bombillas|Solución]] | ||
| Línea 58: | Línea 70: | ||
[[Condensador con pérdidas|Solución]] | [[Condensador con pérdidas|Solución]] | ||
<!-- | |||
==Condensador con dos capas no ideales== | ==Condensador con dos capas no ideales== | ||
Entre dos placas perfectamente conductoras de sección <math>S</math> separadas una distancia <math>a+b</math> se encuentran dos capas de dieléctricos no ideales de espesores <math>a</math> y <math>b</math> respectivamente. Los dieléctricos tienen permitividades <math>\varepsilon_1</math> y <math>\varepsilon_2</math> y conductividades <math>\sigma_1</math> y <math>\sigma_2</math>, respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m. <math>\mathcal{E}</math>. | Entre dos placas perfectamente conductoras de sección <math>S</math> separadas una distancia <math>a+b</math> se encuentran dos capas de dieléctricos no ideales de espesores <math>a</math> y <math>b</math> respectivamente. Los dieléctricos tienen permitividades <math>\varepsilon_1</math> y <math>\varepsilon_2</math> y conductividades <math>\sigma_1</math> y <math>\sigma_2</math>, respectivamente. Entre las placas se aplica una diferencia de potencial constante mediante de una fuente de f.e.m. <math>\mathcal{E}</math>. | ||
| Línea 70: | Línea 82: | ||
[[Condensador con dos capas no ideales|Solución]] | [[Condensador con dos capas no ideales|Solución]] | ||
--> | |||
==Sistema de 5 resistencias== | ==Sistema de 5 resistencias== | ||
| Línea 87: | Línea 100: | ||
Dado el sistema de resistencias de la figura, calcule la intensidad de corriente que entra por el extremo A en los siguientes casos: | Dado el sistema de resistencias de la figura, calcule la intensidad de corriente que entra por el extremo A en los siguientes casos: | ||
<center>[[Archivo:5-resistencias.png| | <center>[[Archivo:5-resistencias.png|500px]]</center> | ||
# {{nivel|1}} En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra. | # {{nivel|1}} En ''A'' se conecta una fuente de 24mV, ''C'' se deja abierto y ''B'' se conecta a tierra. | ||
# {{nivel|1}} En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra. | # {{nivel|1}} En ''A'' se conecta una fuente de 24mV, ''B'' se deja abierto y ''C'' se conecta a tierra. | ||
# {{nivel|1}} En A se conecta una fuente de 24mV, B y C se conectan a tierra. | # {{nivel|1}} En ''A'' se conecta una fuente de 24mV, ''B'' y ''C'' se conectan a tierra. | ||
# {{nivel|2}} En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra. | # {{nivel|2}} En ''A'' se conecta una fuente de 24mV, en ''C'' una de 6mV y ''B'' se conecta a tierra. | ||
# {{nivel|2}} En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra. | # {{nivel|2}} En ''A'' se conecta una fuente de 24mV, en ''B'' una de −24mV y ''C'' se conecta a tierra. | ||
# {{nivel|2}} En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra. | # {{nivel|2}} En ''A'' se conecta una fuente de 24mV, en ''C'' una de −24mV y ''B'' se conecta a tierra. | ||
[[Cinco resistencias iguales|Solución]] | [[Cinco resistencias iguales|Solución]] | ||
==Circuito con dos fuentes y tres resistores== | |||
Calcule las intensidades que circulan por cada una de los tres resistores en el circuito de dos mallas de la figura. | |||
<center>[[Archivo:2-fuentes-3-resistores.png|500px]]</center> | |||
[[Circuito con dos fuentes y tres resistores|Solución]] | |||
==Circuito con cuatro resistores y un condensador== | |||
Se tiene el circuito de la figura, formado por cuatro resistores, un condensador y una fuente de tensión continua. En este estado de corriente continua, | |||
# ¿cuál es la lectura del voltímetro de la figura? | |||
# ¿Cuál sería la lectura de voltímetros situados en cada uno de los otros resistores y en el condensador? | |||
# ¿Qué intensidades de corriente medirían amperímetros situados tras cada uno de los resistores? | |||
<center>[[Archivo:4-resistores-1-condensador.png|800px]]</center> | |||
[[Circuito con cuatro resistores y un condensador|Solución]] | |||
==Esfera unida a tres resistores== | |||
Una esfera metálica de radio ''b'' está conectada a tres resistores iguales de resistencia ''R''. Uno de estos resistores está conectado por su otro extremo a una fuente de tensión <math>V_0>0</math> y los otros dos tienen su otro extremo conectado a tierra. En un instante dado la tensión a la que se encuentra la esfera es <math>3V_0/4</math>. Para ese instante… | |||
# ¿Está aumentando o disminuyendo la carga de la esfera? ¿Cuánto valen ''Q'' y <math>\mathrm{d}Q/\mathrm{d}t</math>? | |||
# ¿Cuánto vale la energía almacenada en ese instante en el sistema? | |||
# ¿Cuánto vale la potencia que se disipa por efecto Joule? | |||
[[Archivo:Esfera-tres-resistores.png|800px|center]] | |||
[[Esfera unida a tres resistores|Solución]] | |||
==Esfera que se conecta a una fuente de tensión== | ==Esfera que se conecta a una fuente de tensión== | ||
| Línea 119: | Línea 159: | ||
[[Potencia de un generador real|Solución]] | [[Potencia de un generador real|Solución]] | ||
<!-- | |||
==Sistema de cuatro hilos== | ==Sistema de cuatro hilos== | ||
Se tiene un sistema de cuatro hilos rectilíneos de sección circular, todos ellos de longitud <math>\ell_0=10\,\mathrm{cm}</math> y hechos de un material de conductividad <math>\sigma=(4/\pi)\times10^{4} \mathrm{S}/\mathrm{m}</math>. Los diámetros de los cables son respectivamente <math>d_1=4\,\mathrm{mm}</math>, <math>d_2=2\,\mathrm{mm}</math>, <math>d_3=2\,\mathrm{mm}</math> y <math>d_4=1\,\mathrm{mm}</math>. Los cuatro hilos están unidos a un nodo común, mientras que sus otros extremos están conectados a fuentes de tensión de voltajes <math>V_1=1.26\,\mathrm{V}</math>, <math>V_2=210\,\mathrm{ | Se tiene un sistema de cuatro hilos rectilíneos de sección circular, todos ellos de longitud <math>\ell_0=10\,\mathrm{cm}</math> y hechos de un material de conductividad <math>\sigma=(4/\pi)\times10^{4} \mathrm{S}/\mathrm{m}</math>. Los diámetros de los cables son respectivamente <math>d_1=4\,\mathrm{mm}</math>, <math>d_2=2\,\mathrm{mm}</math>, <math>d_3=2\,\mathrm{mm}</math> y <math>d_4=1\,\mathrm{mm}</math>. Los cuatro hilos están unidos a un nodo común, mientras que sus otros extremos están conectados a fuentes de tensión de voltajes <math>V_1=1.26\,\mathrm{V}</math>, <math>V_2=210\,\mathrm{mV}</math> o a tierra, tal como indica la figura. Inicialmente el interruptor A está cerrado. | ||
<center>[[Archivo:cuatro-hilos.png|600px]]</center> | <center>[[Archivo:cuatro-hilos.png|600px]]</center> | ||
| Línea 135: | Línea 176: | ||
[[Sistema de cuatro hilos|Solución]] | [[Sistema de cuatro hilos|Solución]] | ||
--> | |||
==Tres resistencias y un condensador== | ==Tres resistencias y un condensador== | ||
Se tiene el sistema de resistencias, condensadores y fuentes de voltaje de la figura. | Se tiene el sistema de resistencias, condensadores y fuentes de voltaje de la figura. | ||
<center>[[Archivo:3R-1C.png| | <center>[[Archivo:3R-1C.png|800px]]</center> | ||
# ¿Cuánto vale la corriente que entra por cada nodo? | # ¿Cuánto vale la corriente que entra por cada nodo? | ||
# ¿Cuánta potencia se consume en el sistema de resistencias? | # ¿Cuánta potencia se consume en el sistema de resistencias? | ||
| Línea 145: | Línea 187: | ||
[[Tres resistencias y un condensador|Solución]] | [[Tres resistencias y un condensador|Solución]] | ||
<!-- | |||
==Circuito en forma de H== | ==Circuito en forma de H== | ||
Un circuito integrado está constituido por una pista de cobre (<math>\sigma\simeq 6.0\times 10^7\,\mathrm{S}/\mathrm{m})</math> de espesor e=0.1 mm montada sobre un dieléctrico. La pista tiene en todos sus tramos un ancho d = 1.0 mm. La pista tiene forma de H, en la que cada tramo mide b = 6.0 cm, salvo el travesaño central, que mide 3cm. | Un circuito integrado está constituido por una pista de cobre (<math>\sigma\simeq 6.0\times 10^7\,\mathrm{S}/\mathrm{m})</math> de espesor e=0.1 mm montada sobre un dieléctrico. La pista tiene en todos sus tramos un ancho d = 1.0 mm. La pista tiene forma de H, en la que cada tramo mide b = 6.0 cm, salvo el travesaño central, que mide 3cm. | ||
| Línea 172: | Línea 214: | ||
[[Circuito en forma de cuadrado|Solución]] | [[Circuito en forma de cuadrado|Solución]] | ||
--> | |||
==Circuito formado por dos cuadrados== | |||
Una espira doble como la ilustrada en la figura, está formada por varillas de 1 mm² de sección transversal y de un material de conductividad <math>\sigma=10^5\,\mathrm{S}/\mathrm{m}</math>. Las longitudes de las varillas son las indicadas en la figura. | |||
Entre las esquinas opuestas del sistema se aplica una diferencia de potencial de 1.4 V. | |||
# Calcule la intensidad de corriente que circula por cada una de las varillas que forman el sistema. | |||
# Si se coloca un voltímetro para medir la d.d.p, entre el nodo central superior y el central inferior (con la polaridad positiva en el nodo superior), ¿cuánto marcará el voltímetro? | |||
# Calcule la resistencia equivalente del conjunto. | |||
# Halle la potencia eléctrica que se está disipando en el sistema por efecto Joule. | |||
[[Archivo:circuito-dos-cuadrados.png|center]] | |||
[[Circuito formado por dos cuadrados|Solución]] | |||
==Corriente en tres hilos paralelos== | |||
Se tiene un sistema formado por tres hilos de constantán, una aleación que tiene conductividad <math>\sigma=2.0 \times 10^6\,\mathrm{S}/\mathrm{m}</math>, los tres hilos son de la misma longitud, <math>\ell=12\,\mathrm{m}</math>. El hilo “1” tiene una sección transversal <math>A_1=3\,\mathrm{mm}^2</math>, el “2” una sección <math>A_2=1\,\mathrm{mm}^2</math> y el “3” una sección <math>A_3=2\,\mathrm{mm}^2</math>. Se disponen paralelamente, con una distancia entre ellos <math>b=10\,\mathrm{cm}</math>. Se conectan como indica la figura, con los interruptores A y B cerrados. Tanto los interruptores como las demás conexiones son ideales, sin resistencia. El hilo “1” se conecta a una fuente de tensión continua <math>V_0=13.2\,V</math> y el “3” a tierra. | |||
Se trata de comparar el estado de corriente continua antes de que se abran los interruptores y el estado de corriente continua después de abrir ambos. | |||
# Calcule la intensidad de corriente que circula por cada uno de los hilos. | |||
## Con los dos interruptores cerrados. | |||
## Con los dos interruptores abiertos. | |||
# Calcule la potencia consumida por efecto Joule en cada uno de los hilos y la total del sistema | |||
## Con los dos interruptores cerrados. | |||
## Con los dos interruptores abiertos. | |||
[[Archivo:corriente-3-hilos-paralelos.png|800px|center]] | |||
[[Corriente en tres hilos paralelos|Solución]] | |||
==Circuito con dos transitorios== | |||
Se tiene el circuito de la figura, formado por un resistor, un condensador, una fuente de tensión y un interruptor. Suponga que inicialmente el condensador está descargado | |||
# En <math>t=0</math> se cierra el interruptor en la posición A. Determine la ecuación diferencial para la carga del condensador como función del tiempo. | |||
# Resuelva esta ecuación diferencial y halle la carga en el condensador y la intensidad de corriente por el resistor como función del tiempo. | |||
# Calcule la energía almacenada en el condensador en el estado de equilibrio final y la energía total disipada en la resistencia durante el proceso de carga y el trabajo total realizado por el condensador en este proceso. | |||
# Suponga que, una vez está el sistema en equilibrio y, sin descargar el condensador, se pasa el interruptor de la posición A a la B. Determine la nueva ecuación diferencial para la carga del condensador. | |||
# Resuelva esta ecuación diferencial y halle la carga del condensador y la intensidad de corriente por el resistor como función del tiempo. | |||
# Para este proceso calcule la energía total disipada en el resistor durante el proceso de descarga. | |||
[[Archivo:circuito-dos-transitorios.png|center]] | |||
[[Circuito con dos transitorios|Solución]] | |||
==EquivalenciaΔ-Y para resistores== | |||
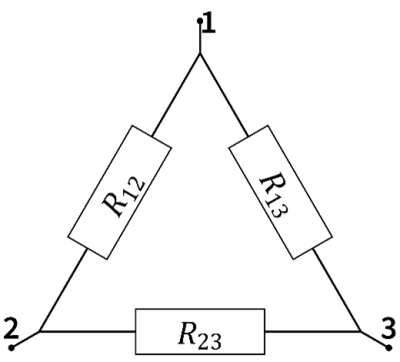
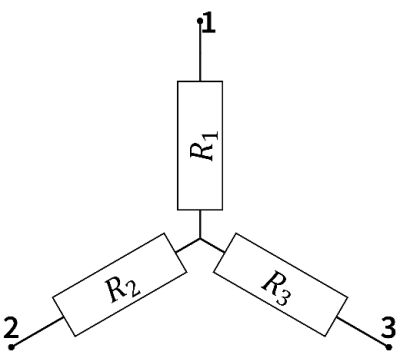
Como en el caso de los condensadores del problema “[[Transformaci%C3%B3n_%CE%94-Y_(delta-estrella)|Transofrmación Δ-Y (delta-estrella)]]”, existe una transformación Δ-Y (delta-estrella) para resistencias (que, de hecho, es la más usual). Se trata de relacionar dos sistemas equivalentes. En la configuración delta tenemos tres resistores formando un triángulo entre tres nodos. En la configuración en estrella tenemos tres resistores unidos a un nodo central sin conexión exterior. | |||
<center> | |||
[[Archivo:circuito-3R-delta.png|400px]] [[Archivo:circuito-3R-estrella.png|400px]] | |||
</center> | |||
# Demuestre que, dadas las resistencias <math>R_1</math>, <math>R_2</math> y <math>R_3</math>, las valores de <math>R_{12}</math>, <math>R_{13}</math> y <math>R_{23}</math> son | |||
<center><math>\begin{array}{ccccc}R_{12}=\dfrac{P}{R_{3}}&\qquad& R_{13}=\dfrac{P}{R_{2}}&\qquad& R_{23}=\dfrac{P}{R_{1}}\\ &&&& \\ | |||
&&P=R_{1} R_{2}+R_{1} R_{3}+R_{2} R_{3}&&\end{array}</math></center> | |||
<ol start=2> | |||
<li>Demuestre las relaciones inversas: dadas las resistencias de la delta, <math>R_{12}</math>, <math>R_{13}</math> y <math>R_{23}</math>, las resistencias de la estrella, <math>R_1</math>, <math>R_2</math> y <math>R_3</math>. vienen dadas por</li> | |||
</ol> | |||
<center><math>\begin{array}{ccccc}R_{1}=\dfrac{R_{12} R_{13}}{S}&\qquad& R_{2}=\dfrac{R_{12} R_{13}}{S}&\qquad& R_{3}=\frac{R_{13} R_{23}}{S}\\ &&&& \\ | |||
&&S=R_{12}+R_{13}+R_{23}&&\end{array}</math></center> | |||
<ol start=3> | |||
<li>Calcule la configuración en estrella equivalente a una configuración delta en la que las resistencias valen <math>R_{12}=100\,\Omega</math>, <math>R_{13}=400\,\Omega</math>, <math>R_{23}=500\,\Omega</math>.</li> | |||
<li>Calcule la configuración en delta equivalente a una configuración en estrella en la cual <math>R_1=30\,\Omega</math>, <math>R_2=20\,\Omega</math>,<math>R_3=12\,\Omega</math>.</li> | |||
<li>Para los apartados (3) y (4), suponga que <math>V_1=10\,V</math>, <math>V_2=5\,V</math>, <math>V_3=0\,V</math>. Para las dos configuraciones equivalentes calcule la potencia disipada por efecto Joule y compruebe que se llega al mismo resultado.</li> | |||
</ol> | |||
[[EquivalenciaΔ-Y para resistores|Solución]] | |||
==Resistencia equivalente de 5 resistores== | |||
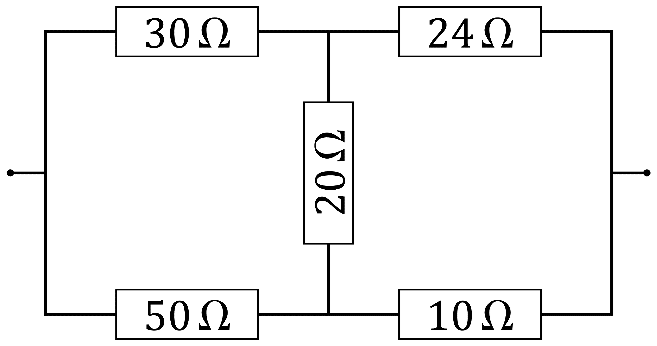
Calcule la resistencia equivalente al sistema de 5 resistores de la figura | |||
[[Archivo:circuito-5-resistores-eq.png|center]] | |||
Revisión actual - 08:59 3 may 2025
Densidad de corriente radial
En una determinada región del espacio alrededor del origen de coordenadas existe una densidad de corriente dependiente de la distancia al origen como
con A y b dos constantes positivas, r la distancia al origen de coordenadas y el vector unitario radial hacia afuera.
- ¿Cuánto vale la derivada respecto al tiempo de la carga contenida en una esfera de radio b/2 con centro el origen? ¿Aumenta o disminuye?
- ¿Y si la esfera tiene radio b?
- ¿Y si tiene radio 2b?
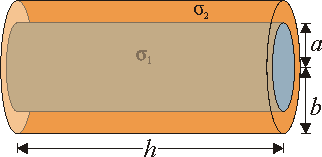
Cable bimetálico
Entre los distintos tipos de cable empleados en la industria, se encuentra el de acero revestido de cobre. Está formado por un núcleo de acero de radio (suponga ), rodeado por una capa de cobre, de radio exterior (sea ).
- Calcule la resistencia de un cable de esta clase de longitud .
- Determine la intensidad de corriente que circula por cada metal cuando se aplica una diferencia de potencial al cable anterior.
Datos: ,
Paso de un pulso de corriente
Por un hilo rectilíneo de gran longitud y resistencia eléctrica circula una corriente variable en el tiempo, tal que su valor es
- Halle la carga que pasa por un punto del hilo entre y .
- Calcule la energía disipada en el cable en el mismo tiempo.
Asociación de dos bombillas en serie
Se colocan en serie dos bombillas de potencias nominales 10 W y 6 W y se conectan a la red. Si la potencia radiada es proporcional a la potencia consumida, ¿cuál de las dos bombillas darán más luz? ¿En qué proporción?
Conexión de tres bombillas
Supongamos que tenemos tres bombillas iguales (simbolizadas por ⊗) de potencia nominal 10W a 240V que se conectan según el esquema siguiente. La fuente es una de continua a 240V.
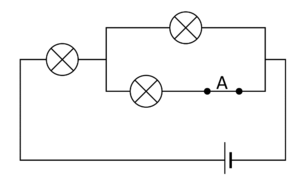
- ¿Cuánta potencia consume cada bombilla? ¿Cuál da más luz? ¿Qué potencia se consume en el circuito completo?
- Si ahora se abre el interruptor A, ¿cómo cambia la potencia consumida por cada bombilla? ¿Y la potencia total consumida?
Triángulo de resistencias
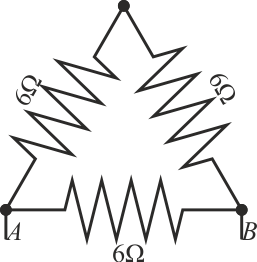
Determine la resistencia equivalente entre los puntos A y B del circuito de tres resistencias de la figura.
Condensador con pérdidas
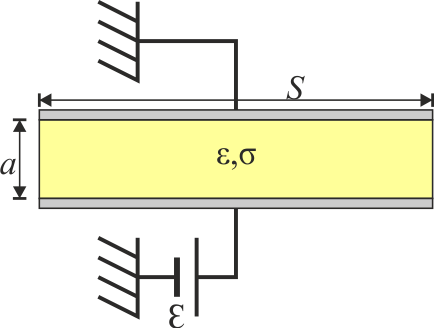
En un modelo de condensador real (“con pérdidas”) se tienen dos placas paralelas perfectamente conductoras de sección , separadas una distancia entre las cuales hay un dieléctrico de permitividad y con una pequeña conductividad . Entre las placas se establece una d.d.p. constante por medio de una fuente de f.e.m .
- Calcule el campo eléctrico y la densidad de corriente entre las placas.
- Halle la energía almacenada en el sistema y la potencia consumida en el dispositivo.
- Diseñe el circuito equivalente a este dispositivo.
- Si la fuente que alimenta a este elemento es una fuente real con f.e.m. y resistencia interna , ¿cuánto valen en ese caso la carga, la corriente, la energía y la potencia?
- Si la d.d.p. que se aplica entre las placas no es continua, sino que varía como , ¿qué corriente llega por el cable al dispositivo?
- ¿Qué ocurre si se desconecta la fuente?
Sistema de 5 resistencias
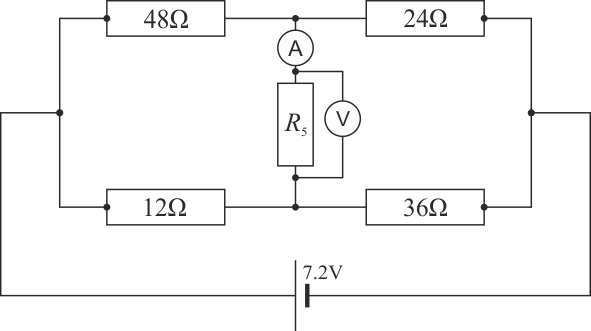
Se tiene el sistema de 5 resistencias de la figura. Entre los extremos de la asociación se aplica una diferencia de potencial de 7.2 V.
- Determine las lecturas del amperímetro y voltímetro de la rama central en los casos:
- Para cada caso, ¿cuánto vale la potencia disipada por efecto Joule en cada resistencia. ¿En cuál de ellas se disipa más energía?
Cinco resistencias iguales
Dado el sistema de resistencias de la figura, calcule la intensidad de corriente que entra por el extremo A en los siguientes casos:
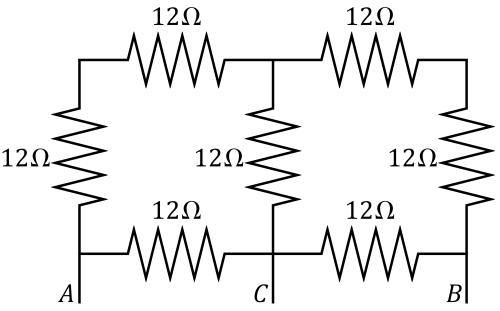
 En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra.
En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra. En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra.
En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra. En A se conecta una fuente de 24mV, B y C se conectan a tierra.
En A se conecta una fuente de 24mV, B y C se conectan a tierra. En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra.
En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra. En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra.
En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra. En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra.
En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra.
Circuito con dos fuentes y tres resistores
Calcule las intensidades que circulan por cada una de los tres resistores en el circuito de dos mallas de la figura.
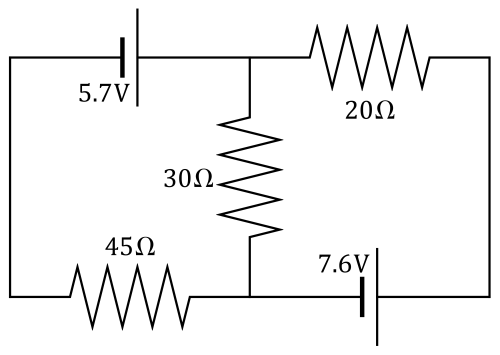
Circuito con cuatro resistores y un condensador
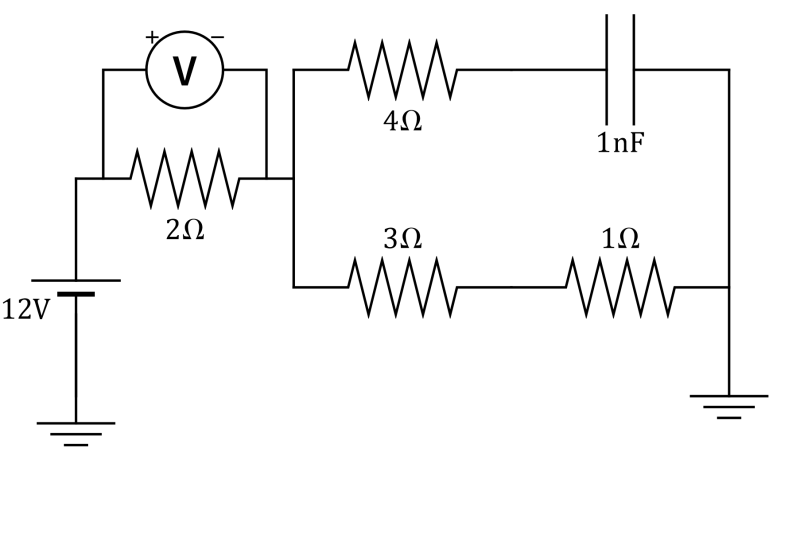
Se tiene el circuito de la figura, formado por cuatro resistores, un condensador y una fuente de tensión continua. En este estado de corriente continua,
- ¿cuál es la lectura del voltímetro de la figura?
- ¿Cuál sería la lectura de voltímetros situados en cada uno de los otros resistores y en el condensador?
- ¿Qué intensidades de corriente medirían amperímetros situados tras cada uno de los resistores?
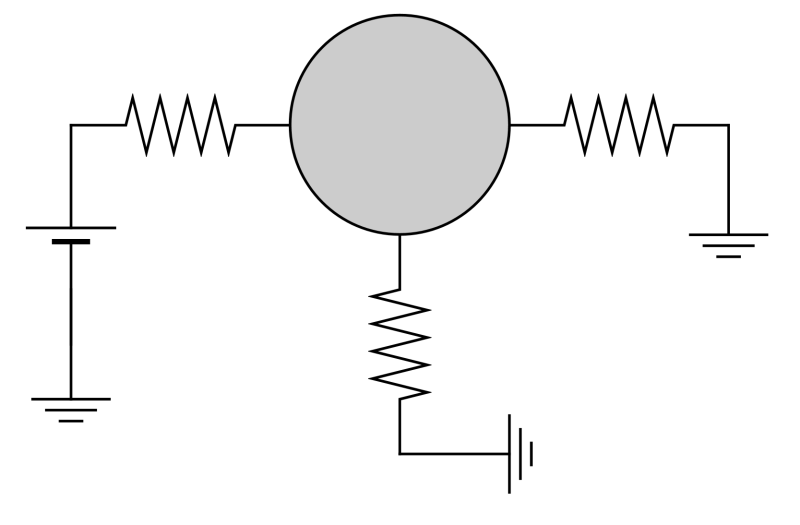
Esfera unida a tres resistores
Una esfera metálica de radio b está conectada a tres resistores iguales de resistencia R. Uno de estos resistores está conectado por su otro extremo a una fuente de tensión y los otros dos tienen su otro extremo conectado a tierra. En un instante dado la tensión a la que se encuentra la esfera es . Para ese instante…
- ¿Está aumentando o disminuyendo la carga de la esfera? ¿Cuánto valen Q y ?
- ¿Cuánto vale la energía almacenada en ese instante en el sistema?
- ¿Cuánto vale la potencia que se disipa por efecto Joule?
Esfera que se conecta a una fuente de tensión
Un conductor metálico esférico de radio 90 cm se encuentra cargado con una carga . Alrededor de la esfera no hay más conductores ni cargas.
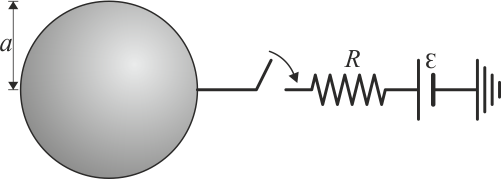
- Halle el potencial al que se encuentra la esfera, así como la energía electrostática almacenada en el sistema.
- Suponga que ahora se conecta a la esfera una fuente de tensión de 0.3 kV, mediante un cable con una resistencia de 100 Ω. Justo tras la conexión, ¿cuánto vale la corriente que circula por el cable? ¿Está aumentando o disminuyendo la carga de la esfera?
- Una vez que se ha alcanzado de nuevo el equilibrio electrostático de la esfera, ¿cuál es su nueva carga? ¿Y la nueva energía almacenada en el sistema?
- ¿Qué trabajo ha realizado la fuente de tensión en el proceso? ¿Cuánta energía se ha disipado en la resistencia?
- Determine la ecuación diferencial que gobierna el potencial de la esfera desde que se conecta la fuente hasta que se llega de nuevo al equilibrio electrostático. Indique como sería la representación gráfica de frente al tiempo.
Dato:
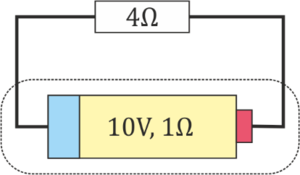
Potencia de un generador real
![]() El generador real de la figura posee una fuerza electromotriz de 10V y una resistencia interna de 1Ω. Cuando se conecta a una resistencia de 4Ω, ¿cuánta potencia eléctrica sale del generador real?
El generador real de la figura posee una fuerza electromotriz de 10V y una resistencia interna de 1Ω. Cuando se conecta a una resistencia de 4Ω, ¿cuánta potencia eléctrica sale del generador real?
Tres resistencias y un condensador
Se tiene el sistema de resistencias, condensadores y fuentes de voltaje de la figura.
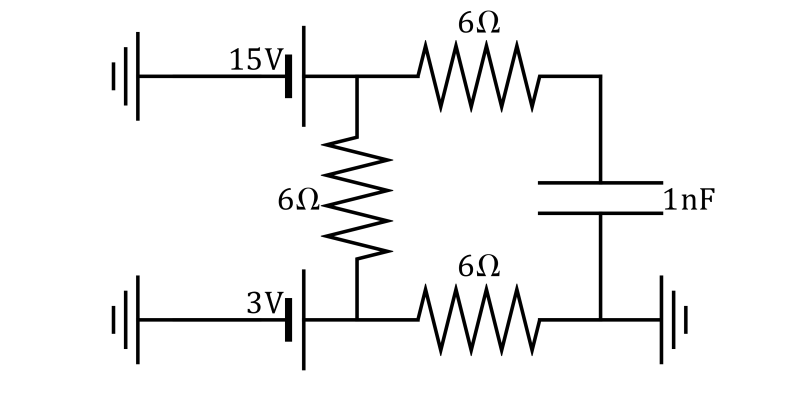
- ¿Cuánto vale la corriente que entra por cada nodo?
- ¿Cuánta potencia se consume en el sistema de resistencias?
- ¿Cuánta energía hay almacenada en el condensador?
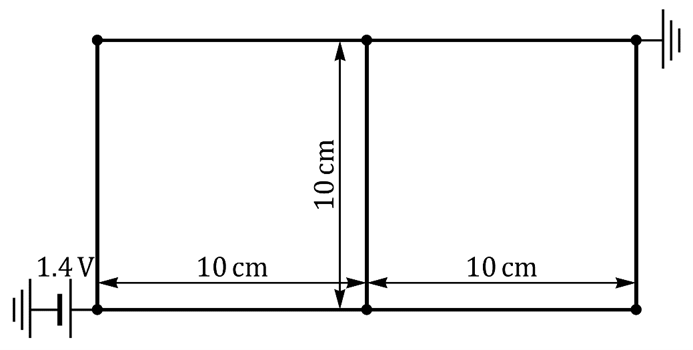
Circuito formado por dos cuadrados
Una espira doble como la ilustrada en la figura, está formada por varillas de 1 mm² de sección transversal y de un material de conductividad . Las longitudes de las varillas son las indicadas en la figura. Entre las esquinas opuestas del sistema se aplica una diferencia de potencial de 1.4 V.
- Calcule la intensidad de corriente que circula por cada una de las varillas que forman el sistema.
- Si se coloca un voltímetro para medir la d.d.p, entre el nodo central superior y el central inferior (con la polaridad positiva en el nodo superior), ¿cuánto marcará el voltímetro?
- Calcule la resistencia equivalente del conjunto.
- Halle la potencia eléctrica que se está disipando en el sistema por efecto Joule.
Corriente en tres hilos paralelos
Se tiene un sistema formado por tres hilos de constantán, una aleación que tiene conductividad , los tres hilos son de la misma longitud, . El hilo “1” tiene una sección transversal , el “2” una sección y el “3” una sección . Se disponen paralelamente, con una distancia entre ellos . Se conectan como indica la figura, con los interruptores A y B cerrados. Tanto los interruptores como las demás conexiones son ideales, sin resistencia. El hilo “1” se conecta a una fuente de tensión continua y el “3” a tierra. Se trata de comparar el estado de corriente continua antes de que se abran los interruptores y el estado de corriente continua después de abrir ambos.
- Calcule la intensidad de corriente que circula por cada uno de los hilos.
- Con los dos interruptores cerrados.
- Con los dos interruptores abiertos.
- Calcule la potencia consumida por efecto Joule en cada uno de los hilos y la total del sistema
- Con los dos interruptores cerrados.
- Con los dos interruptores abiertos.
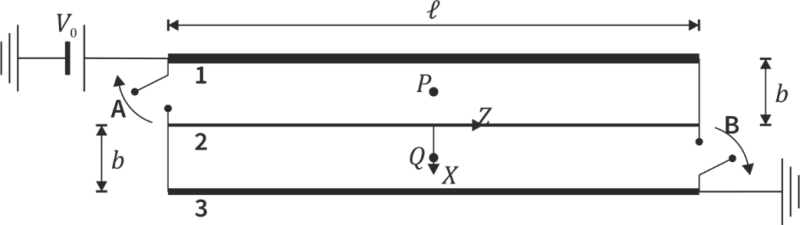
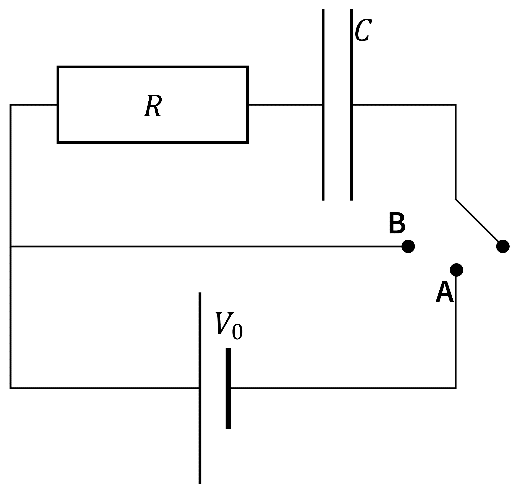
Circuito con dos transitorios
Se tiene el circuito de la figura, formado por un resistor, un condensador, una fuente de tensión y un interruptor. Suponga que inicialmente el condensador está descargado
- En se cierra el interruptor en la posición A. Determine la ecuación diferencial para la carga del condensador como función del tiempo.
- Resuelva esta ecuación diferencial y halle la carga en el condensador y la intensidad de corriente por el resistor como función del tiempo.
- Calcule la energía almacenada en el condensador en el estado de equilibrio final y la energía total disipada en la resistencia durante el proceso de carga y el trabajo total realizado por el condensador en este proceso.
- Suponga que, una vez está el sistema en equilibrio y, sin descargar el condensador, se pasa el interruptor de la posición A a la B. Determine la nueva ecuación diferencial para la carga del condensador.
- Resuelva esta ecuación diferencial y halle la carga del condensador y la intensidad de corriente por el resistor como función del tiempo.
- Para este proceso calcule la energía total disipada en el resistor durante el proceso de descarga.
EquivalenciaΔ-Y para resistores
Como en el caso de los condensadores del problema “Transofrmación Δ-Y (delta-estrella)”, existe una transformación Δ-Y (delta-estrella) para resistencias (que, de hecho, es la más usual). Se trata de relacionar dos sistemas equivalentes. En la configuración delta tenemos tres resistores formando un triángulo entre tres nodos. En la configuración en estrella tenemos tres resistores unidos a un nodo central sin conexión exterior.
- Demuestre que, dadas las resistencias , y , las valores de , y son
- Demuestre las relaciones inversas: dadas las resistencias de la delta, , y , las resistencias de la estrella, , y . vienen dadas por
- Calcule la configuración en estrella equivalente a una configuración delta en la que las resistencias valen , , .
- Calcule la configuración en delta equivalente a una configuración en estrella en la cual , ,.
- Para los apartados (3) y (4), suponga que , , . Para las dos configuraciones equivalentes calcule la potencia disipada por efecto Joule y compruebe que se llega al mismo resultado.
Resistencia equivalente de 5 resistores
Calcule la resistencia equivalente al sistema de 5 resistores de la figura