Disco deslizando por barra horizontal con muelle
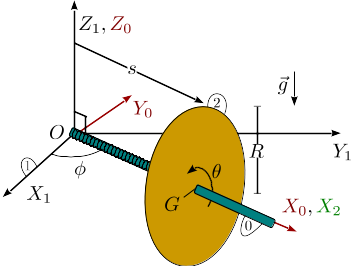
El disco plano de la figura, (sólido "2", masa , radio ) desliza sin rozamiento sobre una barra rígida (sólido "0") de masa despreciable, a la vez que rota alrededor de ella. A su vez esta barra, que permanece siempre en el plano , rota alrededor el eje . Un muelle de constante elástica y longitud natural conecta el punto con el centro del disco. En el instante inicial se tiene , , , , .
- Determina la reducción cinemática del centro de masas del sólido "2" (punto ) en su movimiento absoluto, así como su derivada temporal.
- Encuentra la expresión de la energía cinética del disco, así como su momento cinético respecto a .
- Haz la desvinculación global del disco en su centro de masas. Indica cuantas incógnitas hay en el problema y que ecuaciones usarías para resolverlo (no hace falta escribir las ecuaciones)
- Encuentra y escribe dos integrales primeras del movimiento.
Disco rodando en cavidad con muelle de torsión
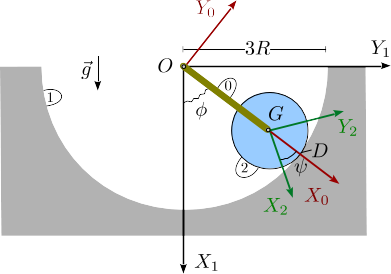
Un disco de radio y masa (sólido "2") rueda sin deslizar sobre una superficie circular cóncava (sólido "1") de radio . En el centro del disco se articula una barra (sólido "0") de masa despreciable y longitud . El otro extremo de la barra se articula en un punto fijo . La barra está conectada a su vez a un resorte de torsión en el punto . Este resorte ejerce un momento sobre la barra, perpendicular al plano de la figura, de modo que la energía potencial asociada a él se puede expresar como , siendo una constante.
- Encuentra la reducción cinemática de los movimientos {01}, {20} y {21}. ¿Cuál es la relación entre y ?.
- Calcula la energía cinética del disco y su energía potencial.
- Escribe la Lagrangiana del sistema y la ecuación diferencial que rige el movimento. Si el ángulo es pequeño, demuestra que el movimiento es armónico simple y encuentra el período de oscilación.
- Estando el disco en reposo y con , se aplica al centro del disco una percusión . Encuentra la velocidad del centro del disco después de la percusión así como el valor mínimo de esta para que el centro del disco llegue hasta el eje. .




















