Segunda Prueba de Control 2011/12 (G.I.C.)

Bala penetrando en un bloque de madera

Una bala de masa $m=10.0\,\mathrm {g}$ viaja con velocidad $v=120\,\mathrm {m/s}$. Impacta con un bloque de madera y penetra en él una distancia $s=2.30\,\mathrm {cm}$- ¿Cuál es el valor aproximado de la fuerza media ejercida por el bloque sobre la bala?

Calcetín oscilante

Un calcetín colgado para recibir un regalo de Navidad mide 128 mm de largo. El único regalo dentro del calcetín es un teléfono móvil. La persona que ha comprado el móvil llama al número del mismo cuando el destinatario del regalo va a recogerlo. Este observa asombrado que el calcetín ́oscila con una amplitud apreciable. ¿Cuál es el valor aproximado de la frecuencia a la que vibra el móvil? (El móvil tiene conectado el vibrador)

Escalera apoyada en una pared

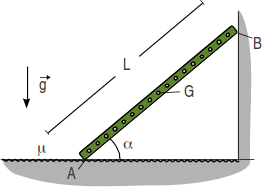
Una escalera de longitud $L$ se apoya en el suelo y una pared vertical de modo que el ángulo que forma con la horizontal es $\alpha$. El contacto con la pared es liso, mientras que con el suelo es rugoso con coeficiente de rozamiento estático $\mu$. La masa de la escalera es $m$, y su peso está aplicado en su centro.

1. En condiciones de equilibrio estático, ¿cuanto vale el módulo de la fuerza de rozamiento en el apoyo en el suelo?
2. ¿Qué condición debe cumplir el ángulo para que la escalera no deslice?

Ejemplo de armadura simple

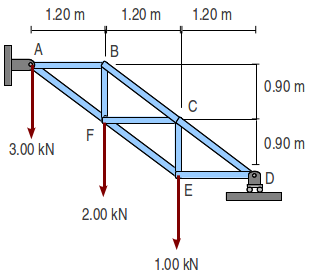
Se tienen la armadura de la figura. Los pesos de las barras son despreciables frente a las cargas.

1. Calcula las reacciones en los apoyos.
2. Calcula la tensión en la barra $BC$.

Partícula sometida a la acción de dos muelles colineales

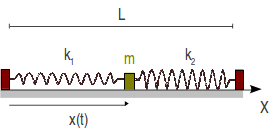
Se tiene el sistema de la figura, formado por dos muelles de longitud natural nula y constantes elásticas $k_{1}$ y $k_{2}$ . Los puntos de anclaje de los muelles están separados por una distancia $L$. Una partícula de masa $m$ está conectada a los dos muelles y se mueve bajo la acción de éstos. El rozamiento con la superficie es despreciable. Los valores numéricos de los parámetros del problema son $k_{1}=100\,\mathrm {N/m}$, $k_{2}=200\,\mathrm {N/m}$, $L=10.0\,\mathrm {cm}$, $m=100\,\mathrm {g}$.

1. Calcula la posición de equilibrio de la partícula.
2. Calcula la energía potencial elástica de la partícula cuando está en su posición de equilibrio.
3. Estando la partícula en la posición de equilibrio, se le da un empujón hacia la derecha de modo que su velocidad inicial es $v_{0}$. ¿Cuál es el período de las oscilaciones de la partícula?
4. Si el valor numérico de la velocidad inicial es $v_{0}=100\,\mathrm {cm/s}$, ¿cuál es la amplitud de las oscilaciones de la partícula?