Segunda Convocatoria Ordinaria 2015/16 (F1 G.I.C.)

Escalera con masa

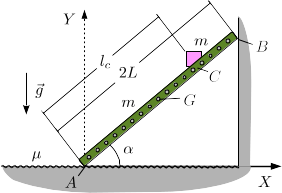
Una escalera homogénea, de masa $m$ y longitud $2L$, está apoyada en el suelo y en una pared vertical como se indica en la figura. El contacto es rugoso en el suelo y liso en la pared. El coeficiente de rozamiento estático entre la escalera y el suelo es $\mu$. Una masa $m$ se sitúa sobre la escalera en el punto $C$, de modo que se encuentra a una distancia $l_{C}$ del punto de apoyo de la escalera en el suelo.

1. Dibuja el diagrama de cuerpo libre del sólido, indicando correctamente el sentido de todas las fuerzas.
2. Considerando $l_{c}$ y $\alpha$ como datos, determina las reacciones vinculares que actúan sobre la escalera.
3. En las condiciones del apartado anterior, ¿que condición debe cumplirse para que el equilibrio sea posible?
4. ¿Que condición debe cumplir el coeficiente de rozamiento estático para que la masa pueda ponerse en cualquier punto de la escalera sin que ésta deslice?

Características cinemáticas de una partícula en movimiento

Una partícula se mueve en el plano $OXY$ de modo que su vector de posición ${\overrightarrow {OP}}$ viene dado por la ley horaria

${\overrightarrow {OP}}\equiv {\vec {r}}(t)=A\,\mathrm {sen} \,(\Omega t)\,{\vec {\imath }}-{\dfrac {A}{2}}\cos(2\Omega t)\,{\vec {\jmath }}$

siendo $A$ y $\Omega$ son constantes conocidas. Consideremos el instante de tiempo $t={\dfrac {\pi }{6\Omega }}$.

1. Calcula la rapidez de la partícula en ese instante.
2. Determina el vector tangente a la trayectoria de la partícula en ese instante.
3. Calcula la componente tangencial de su aceleración en ese instante.
4. Encuentra el radio de curvatura de su trayectoria en ese instante.

Colisión inelástica sobre un muelle

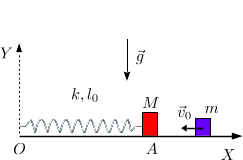
Una masa $m$ se dirige hacia una masa $M$ en reposo con velocidad de módulo $v_{0}$, como se indica en la figura. La masa $M$ se encuentra conectada a un resorte ideal de constante elástica $k$ y longitud natural $l_{0}$, anclado en el punto $O$. Antes de la colisión el muelle está relajado. El contacto con el suelo es liso en todo momento.

1. Suponiendo que la colisión transcurre durante un tiempo $\Delta t$ muy pequeño, y que es completamente inelástica, determina la velocidad de las dos masas justo después de la colisión. Calcula también la fuerza media ejercida sobre la masa $M$ durante la colisión.
2. Supongamos a partir de ahora que las dos masas son iguales $M=m=m_{0}$. ¿Cuál es el valor mínimo de $v_{0}$ para que las dos masas llegen hasta el eje $OY$?
3. Determina el vector de posición, la velocidad y la aceleración del conjunto formado por las dos masas para un instante de tiempo arbitrario después de la colisión.

Masa sobre plano inclinado con muelle

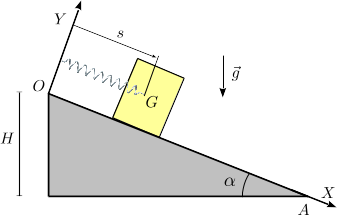
Un bloque de masa $M$ está en reposo en lo alto de un plano inclinado. El bloque está enganchado a un muelle ideal de constante elástica $k$ y longitud natural nula, anclado en el punto más alto del plano inclinado. El bloque comienza a deslizar por el plano inclinado como se indica en la figura. El muelle se mantiene siempre horizontal al plano inclinado. El sistema está sometido a la acción de la gravedad.

1. Dibuja las fuerzas que actúan sobre el disco, indicando correctamente su dirección y sentido, con y sin rozamiento entre el disco y el plano.
2. En el caso de que no haya rozamiento, determina el punto en que se para el bloque. ¿Que condición debe cumplir $k$ para que lo haga antes de llegar al punto $A$?
3. Repite el análisis del apartado anterior si hay un rozamiento entre el bloque y el plano, caracterizado por un coeficiente de rozamiento dinámico $\mu$.