Masa sobre plano inclinado con muelle, Septiembre 2016 (F1 G.I.C.)

Enunciado

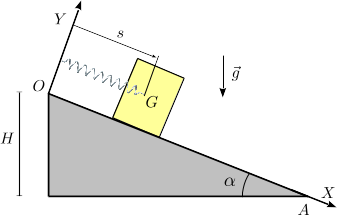
Un bloque de masa $M$ está en reposo en lo alto de un plano inclinado. El bloque está enganchado a un muelle ideal de constante elástica $k$ y longitud natural nula, anclado en el punto más alto del plano inclinado. El bloque comienza a deslizar por el plano inclinado como se indica en la figura. El muelle se mantiene siempre horizontal al plano inclinado. El sistema está sometido a la acción de la gravedad.

1. Dibuja las fuerzas que actúan sobre el disco, indicando correctamente su dirección y sentido, con y sin rozamiento entre el disco y el plano.
2. En el caso de que no haya rozamiento, determina el punto en que se para el bloque. ¿Que condición debe cumplir $k$ para que lo haga antes de llegar al punto $A$?
3. Repite el análisis del apartado anterior si hay un rozamiento entre el bloque y el plano, caracterizado por un coeficiente de rozamiento dinámico $\mu$.

Solución

Fuerzas sobre el bloque

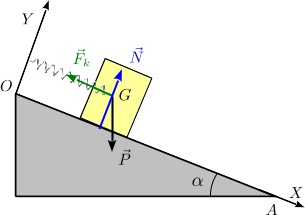
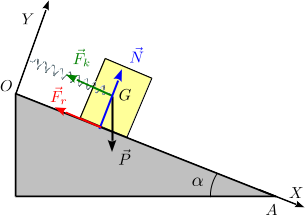
Las figuras muestran las fuerzas que actúan sobre el bloque sin rozamiento (arriba ) y con rozamiento (abajo). En las dos situaciones tenemos el peso del bloque, la reacción vincular del plano y la fuerza del muelle. Cuando hay rozamiento se añade la fuerza de rozamiento, tangente al plano. En este caso sabemos que va dirigida hacia arriba, pues el bloque empieza a deslizar hacia abajo y la fuerza de rozamiento se opone al movimiento relativo entre las superficies.

Las expresiones de las fuerzas son, en los ejes indicados en la figura

${\begin{array}{l}{\vec {P}}=Mg\,\mathrm {sen} \,\alpha \,{\vec {\imath }}-Mg\cos \alpha \,{\vec {\jmath }}\\\\{\vec {N}}=N\,{\vec {\jmath }}\\\\{\vec {F}}_{k}=-ks\,{\vec {\imath }}\\\\{\vec {F}}_{r}=-F_{r}\,{\vec {\imath }}\end{array}}$

Movimiento sin rozamiento

Si no hay rozamiento sólo el peso y el muelle realizan trabajo. Como son conservativas, se conserva la energía mecánica.

Para calcular la energía potencial gravitatoria escogemos como origen de potencial el punto más alto del plano. Entonces

$U_{g}=-Mgs\,\mathrm {sen} \,\alpha$

Para la energía potencial elástica tenemos

$U_{k}={\dfrac {1}{2}}ks^{2}$

Como el bloque parte del reposo, en el instante inicial la energía mecánica es

$E=U_{g}(s=0)+U_{k}(s=0)=0\,$

Para una posición definida por el valor de $s$ la energía mecánica es

${\dfrac {1}{2}}M{\dot {s}}^{2}-Mgs\,\mathrm {sen} \,\alpha +{\dfrac {1}{2}}ks^{2}$

Igualando las dos expresiones obtenemos

${\dot {s}}^{2}=2gs\,\mathrm {sen} \,\alpha -{\dfrac {k}{M}}s^{2}$

Para que el bloque se pare debe ocurrir ${\dot {s}}=0$. Obtenemos dos valores de $s$ para los que se cumple esto

$s=s_{1}=0,\qquad s=s_{2}={\dfrac {2Mg}{k}}\,\mathrm {sen} \,\alpha$

El valor $s_{1}$ corresponde al instante inicial. El segundo es cuándo se para el bloque en la rampa. Para que se detenga antes del final de ésta debe ocurrir

$s_{2}\leq {\dfrac {H}{\mathrm {sen} \,\alpha }}\Longrightarrow k\geq {\dfrac {2Mg}{H}}\,\mathrm {sen} ^{2}\alpha$

Movimiento con rozamiento

En este caso la fuerza de rozamiento, que no es conservativa, realiza trabajo. Entonces no se conserva la energía mecánica. Pero podemos calcular el trabajo realizado por la fuerza de rozamiento y aplicar

$\Delta E=W_{roz}$

Tenemos que determinar la fuerza de reacción vincular del plano para calcular el trabajo de rozamiento. Aplicamos la segunda ley de Newton al movimiento del bloque

$M{\vec {a}}={\vec {P}}+{\vec {N}}+{\vec {K}}_{k}+{\vec {F}}_{r}\Longrightarrow \left\{{\begin{array}{lcl}(X)&\to &M{\ddot {s}}=Mg\,\mathrm {sen} \,\alpha -ks-F_{r}\\&&\\(Y)&\to &0=N-Mg\cos \alpha \end{array}}\right.$

Entonces

$N=Mg\cos \alpha$

En el régimen dinámico, la fuerza de rozamiento es

${\vec {F}}_{r}=-\mu |{\vec {N}}|\,{\vec {\imath }}=-\mu Mg\cos \alpha$

El trabajo realizado por la fuerza de rozamiento en el desplazamiento es

$W_{roz}=\int \limits _{0}^{s}{\vec {F}}_{r}\cdot \mathrm {d} {\vec {r}}=-\int \limits _{0}^{s}\mu Mg\cos \alpha \mathrm {d} x=-\mu Mgs\cos \alpha$

Aplicado el balance de energía-trabajo tenemos

$\Delta E=E(s)-E(0)=-\mu Mgs\cos \alpha$

Usando las expresiones anteriores de la energía mecánica tenemos

${\dot {s}}^{2}=2gs(\mathrm {sen} \alpha -\mu \cos \alpha )-{\dfrac {k}{M}}s^{2}$

El bloque se para en los puntos en que ${\dot {s}}=0$. Eso nos da un ecuaicón que tiene dos soluciones

$s=s_{1}=0,\qquad s=s_{2}={\dfrac {2Mg}{k}}\,(\mathrm {sen} \,\alpha -\mu \cos \alpha )$

El primer valor corresponde al instante inicial. El segundo es donde se para el bloque. Para que se detenga antes del fin del plano debe ocurrir

$s_{2}\leq {\dfrac {M}{\mathrm {sen} \,\alpha }}\Longrightarrow k\geq {\dfrac {2Mg}{H}}{\dfrac {\,(\mathrm {sen} \,\alpha -\mu \cos \alpha )}{\mathrm {sen} \,\alpha }}$

El valor mínimo de $k$ es menor que en el apartado anterior, debido a la energía disipada por el rozamiento.