Segunda Convocatoria 2016/17 (G.I.C.)

Placa cuadrada pivotando conectada a un muelle

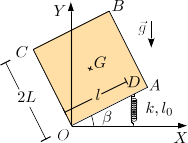
Una placa cuadrada homogénea de masa $m$ y lado $2L$ se apoya sobre uno de sus extremos, el punto $O$ de la figura. Este vértice de la placa no se mueve nunca. Un muelle de constante elástica $k$ y longitud natural $l_{0}=L$ está conectado a un punto $D$ del lado $OA$ de la placa. El otro extremo del muelle está en el eje $OX$, de modo que el muelle es siempre vertical. La gravedad actúa como se indica en la figura. La masa de la placa es tal que $mg=kL$.

1. Dibuja el diagrama de cuerpo libre del sólido rígido.
2. Encuentra las expresiones de las fuerzas que actúan sobre la placa.
3. Si tenemos $\beta =\pi /3$, encuentra el valor de $l$ para el que la placa está en equlibrio.
4. Suponiendo que $\beta =\pi /4$, calcula el par de fuerzas que habría que aplicar sobre la placa para que esté en equilibrio cuando el punto $D$ coincide con el $A$ (el muelle siempre está vertical). Encuentra también el valor de las fuerzas vinculares en esta situación.

Masa en barra fija con muelle

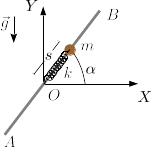
Una partícula de masa $m$ puede moverse a lo largo de una barra de longitud $L$. La partícula está conectada al extremo de un muelle de constante elástica $k$ y longitud natural nula. El ángulo que forma la barra con el eje horizontal $OX$ es $\alpha$, y no cambia con el tiempo. La gravedad actúa como se indica en la figura. El coeficiente de rozamiento estático entre la partícula y la barra es $\mu$.

1. Dibuja el diagrama de cuerpo libre de la partícula, así como la expresión de las fuerzas que actúan sobre ella.
2. Suponiendo que no hay rozamiento, determina el valor de equilibrio de $s$ ($s=0$ corresponde al punto $O$ de la barra).
3. Si ahora incluimos el rozamiento, calcula el rango posible de valores de equilibrio de $s$.
4. Supongamos de nuevo que no hay rozamiento. Encuentra la expresión del vector velocidad y aceleración de la partícula.
5. Aplicando la Segunda Ley de Newton, encuentra la ecuación de movimiento, así como la frecuencia de las oscilaciones.

Masa en barra rotando con muelle

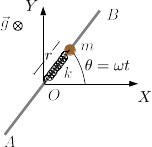
Una partícula de masa $m$ puede moverse a lo largo de una barra de longitud $L$. La partícula está conectada al extremo de un muelle de constante elástica $k$ y longitud natural $l_{0}$. El ángulo que forma la barra con el eje horizontal $OX$ es $\theta =\omega t$, donde $\omega$ es una constante conocida. La barra se situá en un plano horizontal, de modo que la gravedad actúa como se indica en la figura. El contacto entre la masa y la barra es liso.

1. Encuentra la expresión de los vectores de posición, velocidad y aceleración de la masa usando las coordenadas y la base polares.
2. Encuentra las expresiones del momento cinético de la masa respecto a $O$ y su energía mecánica.
3. Determina el valor de $r$ para el que la masa no se mueve respecto a la barra. ¿Cuanto vale la fuerza de reacción vincular en este caso? ¿Que ocurre si $\omega >{\sqrt {k/m}}$?.
4. Encuentra la ecuación diferencial de movimiento para $r(t)$. ¿Que condición debe cumplirse para que el movimiento sea armónico simple?