Masa en barra rotando con muelle, Sept 2017 (G.I.C.)

Enunciado

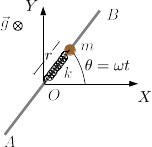
Una partícula de masa $m$ puede moverse a lo largo de una barra de longitud $L$. La partícula está conectada al extremo de un muelle de constante elástica $k$ y longitud natural $l_{0}$. El ángulo que forma la barra con el eje horizontal $OX$ es $\theta =\omega t$, donde $\omega$ es una constante conocida. La barra se situá en un plano horizontal, de modo que la gravedad actúa como se indica en la figura. El contacto entre la masa y la barra es liso.

1. Encuentra la expresión de los vectores de posición, velocidad y aceleración de la masa usando las coordenadas y la base polares.
2. Encuentra las expresiones del momento cinético de la masa respecto a $O$ y su energía mecánica.
3. Determina el valor de $r$ para el que la masa no se mueve respecto a la barra. ¿Cuanto vale la fuerza de reacción vincular en este caso? ¿Que ocurre si $\omega >{\sqrt {k/m}}$?.
4. Encuentra la ecuación diferencial de movimiento para $r(t)$. ¿Que condición debe cumplirse para que el movimiento sea armónico simple?

Solución

Vectores posición velocidad y aceleración

La expresión genérica de los vectores posición, velocidad y aceleración en coordenadas polares es

${\begin{array}{l}{\vec {r}}=r\,{\vec {u}}_{r}\\{\vec {v}}={\dot {r}}\,{\vec {u}}_{r}+r{\dot {\theta }}\,{\vec {u}}_{\theta }\\{\vec {a}}=({\ddot {r}}-r{\dot {\theta }}^{2})\,{\vec {u}}_{r}+(2{\dot {r}}{\dot {\theta }}+r{\ddot {\theta }})\,{\vec {u}}_{\theta }\end{array}}$

En este caso, como la partícula está obligada a permanecer en la barra, tenemos

$\theta =\omega t,\qquad {\dot {\theta }}=\omega ,\qquad {\ddot {\theta }}=0.$

Entonces, los vectores pedidos son

${\begin{array}{l}{\vec {r}}=r\,{\vec {u}}_{r}\\{\vec {v}}={\dot {r}}\,{\vec {u}}_{r}+r\omega \,{\vec {u}}_{\theta }\\{\vec {a}}=({\ddot {r}}-r\omega ^{2})\,{\vec {u}}_{r}+(2{\dot {r}}\omega )\,{\vec {u}}_{\theta }\end{array}}$

Momento cinético respecto a $O$ y energía mecánica

El momento cinético (o angular) respecto a $O$ es

${\vec {L}}_{O}={\vec {r}}\times (m{\vec {v}})=mr^{2}\omega \,{\vec {k}}$

La energía cinética es

$T={\dfrac {1}{2}}mv^{2}={\dfrac {m}{2}}\,\left({\dot {r}}^{2}+r^{2}\omega ^{2}\right)$

La altura de la masa respecto a la gravedad no cambia, por lo que la energía potencial gravitatoria es constante y podemos tomarla como cero. La energía potencial es íntegrametne elástica

$U=U_{k}={\dfrac {1}{2}}k(r-l_{0})^{2}$

La energía mecánica es

$E=T+U={\dfrac {m}{2}}\,\left({\dot {r}}^{2}+r^{2}\omega ^{2}\right)+{\dfrac {1}{2}}k(r-l_{0})^{2}$

Equilibrio respecto a la barra

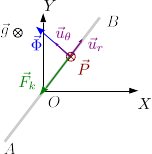
La figura de la derecha muestra las fuerzas que actúan sobre la barra: el peso, la fuerza elástica del muelle y la fuerza vincular normal a la barra. En la base polar se pueden expresar como

${\begin{array}{l}{\vec {P}}=-mg\,{\vec {k}}\\{\vec {F}}_{k}=-k(r-l_{0})\,{\vec {u}}_{r}\\{\vec {\Phi }}=N_{\theta }\,{\vec {u}}_{\theta }+N_{z}\,{\vec {k}}\end{array}}$

La partícula se mueve, pues lo hace la barra. El movimiento está determinado por la Segunda Ley de Newton

$m{\vec {a}}={\vec {P}}+{\vec {F}}_{k}+{\vec {\Phi }}\Longrightarrow \left\{{\begin{array}{lclr}({\vec {u}}_{r})&\to &m({\ddot {r}}-r\omega ^{2})=-k(r-l_{0})&(1)\\({\vec {u}}_{\theta })&\to &2m\omega {\dot {r}}=N_{\theta }&(2)\\({\vec {k}})&\to &0=N_{z}-mg&(3)\\\end{array}}\right.$

Para que la masa no se mueva respecto de la barra debe ocurrir

$r=r_{eq}=\mathrm {cte} \Longrightarrow {\dot {r}}={\ddot {r}}=0$

Imponiendo esta condición en la ecuación (1) obtenemos

$r_{eq}={\dfrac {kl_{0}}{k-m\omega ^{2}}}$

Este valor debe ser positivo. Entonces, si $\omega >{\sqrt {k/m}}$ esta expresión es negativa, y el equilibrio que se busca no es posible.

En la situación de equilibrio la fuerza vincular es

${\vec {\Phi }}=mg\,{\vec {k}}$

Ecuación de movimiento

La ecuación de movimiento es la ecuación (1) del apartado anterior. Podemos reescribirla como

${\ddot {r}}=-\left({\dfrac {k}{m}}-\omega ^{2}\right)\,r+{\dfrac {kl_{0}}{m}}$

Para que sea la ecuación de un oscilador armónico debe ocurrir que el paréntesis que multiplica a $r$ sea positivo, es decir

$\omega <{\sqrt {\dfrac {k}{m}}}$

El término de la derecha es la frecuencia natural de oscilación del muelle si la barra no se mueve. Cuando se cumple esta condición las soluciones son senos y cosenos, y el movimiento está acotado, es decir, la partícula oscila alrededor de una posición de equilibrio (la encontrada en el apartado anterior)

Si esta condición no se cumple, las soluciones son de la forma de senos y cosenos hiperbólicos, es decir, funciones exponenciales crecientes en el tiempo. Intuitivamente, si la barra gira muy rápido, el muelle no es capaz de retener la partícula y esta se desplaza alejándose del centro de la barra.