Problemas de Geometría de masas del sólido rígido (MR G.I.C.) (Ingeniería Civil)
Última edición de la página hace 1 año por Pedro
Problemas del boletín
Aro centrado en el origen
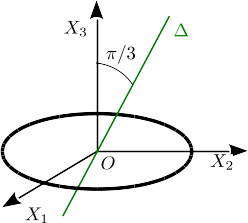
Tenemos un aro homogéneo de masa y radio con centro . Se escogen los ejes coordenadas como se indica en la figura.
- Calcula la matriz de inercia en , usando los ejes indicados en la figura.
- Calcula el momento de inercia respecto a un eje que pasa por y forma un ángulo de con el eje .
- El aro gira alrededor del eje anterior con un vector rotación paralelo al eje. Calcula el momento cinético en y la energía cinética del aro.
Tres barras con simetría
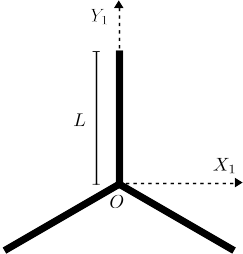
El sistema de la figura es un modelo muy simplificado de hélice de un aerogenerador. Consta de tres barras iguales, de masas y longitud , soldadas en el punto , de modo que forman un sólo sólido rígido. El ángulo entre las tres barras es el mismo.
- Calcula el momento de inercia respecto al eje en .
- Calcula el tensor de inercia en .
- El sólido rota alrededor de un eje que pasa por , está contenido en el plano y forma un ángulo con el eje . Calcula el momento de inercia del sólido alrededor de ese eje.
- Si el vector de rotación tiene módulo y apunta hacia los sentidos positivos de los ejes y , calcula el coseno del ángulo que forman el momento cinético y el vector rotación.
- En este último caso, calcula la energía cinética.
Otros problemas
Momento de inercia de un sólido compuesto de cuatro barras y un aro
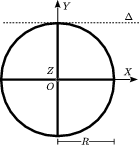
El sólido de la figura está compuesto de un aro delgado de masa y radio , así como de cuatro barras delgadas, cada una de masa y longitud , dispuestas como se indica en la figura. Todos los cuerpos son homogéneos.
- Calcula el momento de inercia .
- Calcula el tensor de inercia en expresado en los ejes cartesianos de la figura.
- Calcula el momento de inercia respecto al eje de la figura.
Tensor de inercia de un hexágono
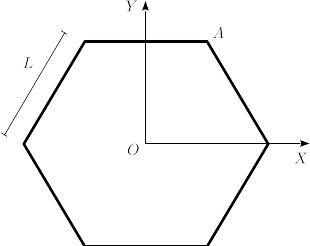
EL sólido rígido de la figura es un hexágono de lado . Cada lado del hexágono tiene una masa .
- Calcula el tensor de inercia del hexágono en su centro, expresado en los ejes de la figura..
- Calcula el tensor de inercia en el vértice , expresado en los mismos ejes.
- Calcula el momento de inercia respecto a un eje paralelo al eje y que pase por .
















