Problemas de Cinemática del sólido rígido (MR G.I.C.)

Problemas del boletín

Campo de velocidades y vector rotación de un sólido rígido

Determine los valores de los parámetros $\lambda$, $\mu$ y $\nu$ para que los vectores

${\vec {v}}_{O}=v_{0}\!\ {\vec {\imath }}\mathrm {;} \quad {\vec {v}}_{A}=\lambda \!\ {\vec {\jmath }}+{\frac {v_{0}}{2}}\ {\vec {k}}\mathrm {;} \quad {\vec {v}}_{B}=v_{0}\!\ {\vec {\imath }}+\mu \!\ {\vec {\jmath }}+\nu \!\ {\vec {k}}$

describan las velocidades instantáneas de tres puntos de un sólido rígido, cuyas posiciones están dadas por las ternas de coordenadas cartesianas, $O(0,0,0$), $A(0,a,0)$ y $B(0,0,b)$. Calcule también las componentes del correspondiente vector rotación instantánea.

Velocidad instantánea en tres puntos

En un determinado instante, tres puntos de un sólido rígido en movimiento ocupan las posiciones dadas por

$O(0,0,0);\qquad A(0,a,0);\qquad B(0,0,2a).$

Las velocidades instantáneas de esos puntos, medidas en el mismo sistema de referencia son:

${\vec {v}}^{O}=v_{0}\,{\vec {\imath }};\qquad {\vec {v}}^{A}={\dfrac {v_{0}}{2}}\,{\vec {k}};\qquad {\vec {v}}^{B}=v_{0}\,({\vec {\imath }}-{\vec {\jmath }}).$

1. Calcula la reducción cinemática en el punto $O$ de dicho movimiento instantáneo y averigua de qué tipo de movimiento se trata.
2. Calcula el vector velocidad instantánea de los puntos con velocidad mínima.
3. Obtén las expresión vectorial del lugar geométrico formado por los puntos con velocidad mínima.

Ejemplos de reducciones cinemáticas

Encuentra las reducciones cinemáticas instantáneas pedidas de cada uno de estos movimientos

1. Una rueda de radio $R$ que gira con velocidad angular constante $\omega$ alrededor de un eje perpendicular a ella que pasa por su centro. Encuentra la reducción canónica.
2. Una rueda de radio $R$ rueda sin deslizar sobre una superficie horizontal de modo que su centro avanza con velocidad uniforme $v_{0}$. Encuentra la reducción en el centro y la reducción canónica.
3. Una rueda de radio $R$ rueda y desliza con velocidad angular $\omega$ alrededor de un eje perpendicular a ella, de modo que el punto de contacto con el suelo tiene una vez relativa a éste de módulo $v_{des}$. Encuentra la reducción en el punto de contacto y la reducción canónica.
4. Un tornillo gira con velocidad angular uniforme $\omega$ y avanza con velocidad uniforme $v$ paralelamente a su eje. Encuentra la reducción en el punto más alto de la superficie frontal del tornillo y la reducción canónica.

Triángulo en movimiento helicoidal

El triángulo de vértices $A$, $B$, y $C$ constituye un sólido rígido en movimiento respecto al sistema de referencia fijo $OXYZ$. De dicho movimiento se conocen los siguientes datos:

1. Los vértices $A$ y $B$ permanecen en todo instante sobre el eje $OZ$, desplazándose ambos con igual velocidad instantánea ${\vec {v}}^{A}={\vec {v}}^{B}=v(t)\,{\vec {k}}$.
2. El vértice $C$ se mueve describiendo la hélice $\Gamma$, que en el sistema $OXYZ$ está descrita por las ecuaciones paramétricas:

$\Gamma :{\vec {r}}={\vec {r}}(\theta )\left\{{\begin{array}{l}x(\theta )=R\,\cos \theta \\y(\theta )=R\,\,\mathrm {sen} \,\theta \\z(\theta )=h\,\theta \\\end{array}}\right.$

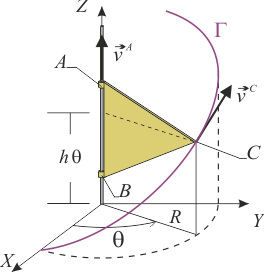
donde $R$ y $h$ son constantes conocidas. Se pide:

1. Indicar de forma razonada cual es el eje instantáneo de rotación y mínimo deslizamiento en este movimiento. Determinar el vector rotación total en términos de los datos expresados en el enunciado.
2. Expresar la componente normal de la aceleración del vértice $C$ en un instante cualquiera, en función de los datos del enunciado.
3. Para el caso en que $v(t)=v_{0}$ (cte), y $h=R/2$, calcular la aceleración del vértice $C$. Determinar la ley horaria $s=s(t)$ con que el punto $C$ describe su trayectoria.

Propiedades cinemáticas instantáneas de pieza triangular

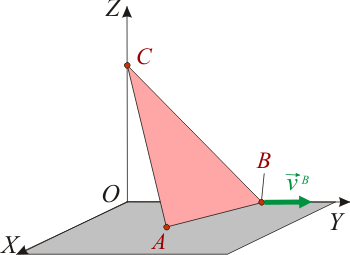
Una pieza triangular $ABC$ se mueve respecto de un sistema de referencia $OXYZ$, comportándose como un sólido rígido. Los vértices $C$ y $B$ de la pieza van recorriendo los ejes $OZ$ y $OY$, respecti-vamente, mientras que el vértice $A$ se desplaza siempre contenido en el plano $OXY$. En un determinado instante, cuando los vértices ocupan las posiciones de coordenadas

$A(a,a,0)\mathrm {;} \quad B(0,2a,0)\mathrm {;} \quad C(0,0,2a)$

la velocidad instantánea del vértice $B$ es ${\vec {v}}^{B}=v_{0}\!\ {\vec {\jmath }}$. Determine, para dicho instante de tiempo:

1. Velocidad del vértice $A$ y vector rotación instantánea.
2. Eje instantáneo de rotación y mínimo deslizamiento.
3. Derivada instantánea del vector rotación, sabiendo que el vértice $B$ se mueve con velocidad instantánea constante.

Disco desenrollándose de una cuerda

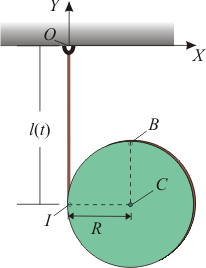
Un disco de radio $R$ gira y cae, siempre contenido en el plano vertical $OXY$, mientras se desenrrolla de una cuerda que pende verticalmente, y cuya longitud aumenta según la ley horaria $l(t)=R+K\!\ t^{2}$ (donde $K$ es una constante conocida).

1. Obtenga la reducción cinemática que describe el movimiento instantáneo del disco.
2. Velocidad y aceleración instantáneas del punto $B$ indicado en la figura.