Problemas del boletín
Aro centrado en el origen
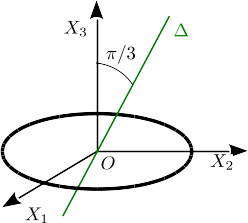
Tenemos un aro homogéneo de masa y radio con centro . Se escogen los ejes coordenadas como se indica en la figura.
- Calcula la matriz de inercia en , usando los ejes indicados en la figura.
- Calcula el momento de inercia respecto a un eje que pasa por y forma un ángulo de con el eje .
- El aro gira alrededor del eje anterior con un vector rotación paralelo al eje. Calcula el momento cinético en y la energía cinética del aro.
Barra articulada rotando en un plano
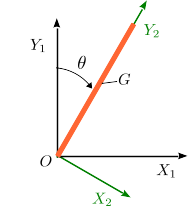
Se tiene una barra homogénea de longitud , masa y radio despreciable. La barra tiene un extremo fijo en el punto y gira únicamente en el plano . La posición de la barra viene determinada por el ángulo que forma con el eje .
- Encuentra la expresión del momento cinético de la barra y de su energía cinética .
- Aplica el T.M.C. en para obtener una ecuación diferencial del movimiento.
- Obtén una integral primera del movimiento. ¿Es equivalente a la ecuación anterior?
Barra articulada rotando en el espacio
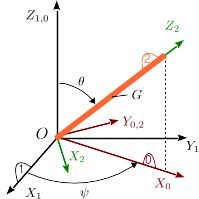
Una barra homogénea de longitud , masa y radio despreciable está articulada en , moviéndose en el espacio tridimensional con su posición descrita mediante las coordenadas , ángulos de precesión y nutación, respectivamente. Escogemos unos ejes solidarios con la barra como se indica en la figura, y unos ejes auxiliares intermedios .
- Encuentra la expresión del momento cinético de la barra.
- Encuentra la expresión de la energía cinética de la barra.















