Momento de inercia de un sólido compuesto de cuatro barras y un aro
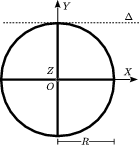
El sólido de la figura está compuesto de un aro delgado de masa y radio , así como de cuatro barras delgadas, cada una de masa y longitud , dispuestas como se indica en la figura. Todos los cuerpos son homogéneos.
- Calcula el momento de inercia .
- Calcula el tensor de inercia en expresado en los ejes cartesianos de la figura.
- Calcula el momento de inercia respecto al eje de la figura.
Barra apoyada sobre placa rectangular
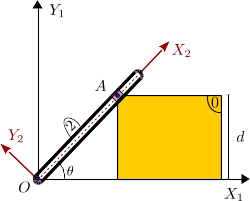
La barra de la figura (sólido "2") está articulada en el punto . Se apoya sobre el vértice de una placa rectangular (sólido "0") de altura . El vértice de la placa puede deslizar a lo largo de la barra. La placa desliza sobre el eje , de forma que su base está siempre en contacto con el eje. El ángulo que forma la barra con el eje es , con constante y positivo.
- Escribe el vector de posición absoluto del punto del sólido "0".
- Encuentra la reducción cinemática de los tres movimientos relativos del sistema.
- Determina aceleración en el instante en que , así como la posición
del C.I.R.











