Primera Convocatoria Ordinaria 2013/14 (G.I.C.)

Masa conectada a dos muelles

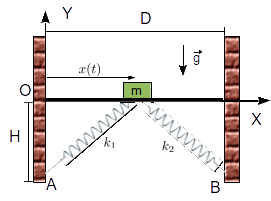
La masa $m$ de la figura puede deslizarse sin rozamiento sobre una superficie horizontal. Conectados a ella hay dos resortes de longitud natural nula y constantes elásticas $k_{1}$ y $k_{2}$. Los muelles están anclados en los puntos $A$ y $B$ respectivamente.

1. Dibuja el diagrama de cuerpo libre de la masa.
2. Encuentra la posición de equilibrio mecánico de la masa.
3. Situamos la masa en su posición de equilibrio. Le damos un empujón hacia la derecha de modo que en $t=0$ el módulo de su velocidad es $v_{0}$. Encuentra la ecuación diferencial que describe el movimiento de la partícula.
4. Encuentra la función que da la posición $x(t)$ de la masa.
5. En el caso $k_{1}=k_{2}$, ¿cuál es el valor máximo de la velocidad para que la partícula no choque con la pared de la derecha?

Barra apoyada en una parede sujeta por un cable

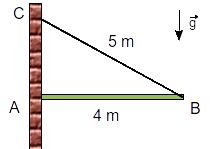
Una barra de longitud $L$ y masa $m$ está sujeta por un extremo a un cable que a su vez tienen su otro extremo anclado en la pared. El otro extremo de la barra se apoya en la pared, de modo que la barra se mantiene horizontal. El contacto en $A$ es rugoso. Determina las fuerzas que actúan sobre la barra en el punto en que se apoya en la pared. ¿Cuál es el valor mínimo del coeficiente de rozamiento para que el equilibrio sea posible? ¿Cuánto vale la tensión del cable en ese caso? El peso de la barra se aplica en su centro de masas.

Partícula recorriendo una espiral

Una partícula recorre una espiral logarítmica con coordenadas polares $r(t)=a\,e^{\theta (t)}$, donde $\theta (t)=\omega t$, Aquí, $t$ es el tiempo y $a$ y $\omega$ son constantes. Encuentra la expresión del vector de posición en coordenadas polares y del triedro intrínseco en cada punto de la trayectoria en función del tiempo. Determina la ley horaria $s(t)$ que da la distancia recorrida por la partícula en función del tiempo.