Enunciado
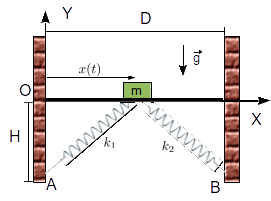
La masa de la figura puede deslizarse sin rozamiento sobre una superficie horizontal. Conectados a ella hay dos resortes de longitud natural nula y constantes elásticas y . Los muelles están anclados en los puntos y respectivamente.
- Dibuja el diagrama de cuerpo libre de la masa.
- Encuentra la posición de equilibrio mecánico de la masa.
- Situamos la masa en su posición de equilibrio. Le damos un empujón hacia la derecha de modo que en el módulo de su velocidad es . Encuentra la ecuación diferencial que describe el movimiento de la partícula.
- Encuentra la función que da la posición de la masa.
- En el caso , ¿cuál es el valor máximo de la velocidad para que la partícula no choque con la pared de la derecha?
Solución
Diagrama de cuerpo libre
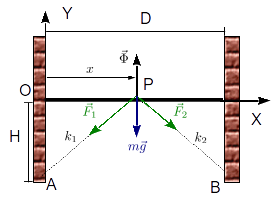
La figura de la derecha muestra las fuerzas que actúan sobre la partícula. Estas son su peso, la fuerza ejercida por cada uno de los muelles y la fuerza de reacción vincular que ejerce la superficie sobre ella. Usando el diedro indicado en la figura la expresión de estas fuerzas es
Hemos utilizado que los muelles tienen longitud natural nula.
Posición de equilibrio
Para obtener la posición de equilibrio aplicamos que la suma de fuerzas debe ser nula.
Obtenemos una ecuación por cada componente
La primera ecuación nos da la posición de equilibrio.
De la segunda obtenemos el valor de la fuerza de reacción vincular
Ecuación de movimiento
Cuando la partícula no está en la posición de equilibrio las fuerzas horizontales de los muelles no se equilibran, por lo que producen una aceleración en la partícula. Como ésta se encuentra siempre sobre la superficie, su aceleración se escribe
La ecuación de movimiento se obtiene aplicando la Segunda Ley de Newton
La componente horizontal es la ecuación diferencial del movimiento
En el instante inicial la partícula está en la posición de equilibrio y tiene velocidad . Las condiciones iniciales son
Solución de la ecuación diferencial
La ecuación diferencial se parece a la de un oscilador armónico. Para que sea igual vamos a describir el movimiento no en función de la coordenada , sino en función de la posición de la partícula respecto a la posición de equilibrio
Derivando respecto al tiempo sucesivamente tenemos
Sustituyendo en la ecuación diferencial y teniendo en cuenta el valor de llegamos a la ecuación
con condiciones iniciales
Esta es la ecuación de un movimiento armónico simple con frecuencia angular
Podemos buscar soluciones de la forma
Derivamos respecto del tiempo
Y aplicamos las condiciones iniciales
Por tanto la posición de la partícula en cada instante viene dada por
Utilizando la variable tenemos
Velocidad máxima para que no choque con la pared
De la expresión de vemos que el valor máximo de la coordenada es
Para que no choque con la pared ese valor debe ser menor o igual que . Por tanto, la condición es
Si consideramos el caso la condición es
Este último apartado puede hacerse también aplicando la conservación de energía mecánica. Vamos a hacerlo en el caso La fuerza de reacción normal no realiza trabajo sobre la partícula, por lo que la energía mecánica se conserva. El movimiento es horizontal, por tanto la energía potencial gravitatoria no cambia. Escogemos como origen de energía potencial gravitatoria.
En el instante inicial, la partícula tiene energía cinética y energía potencial elástica debida a los muelles. Si las dos constantes son iguales tenemos
Y la energía mecánica en el instante inicial es
El caso límite para que no choque con la pared es que su velocidad al llegar a ella sea cero. En ese caso la energía mecánica justo cuando llega a la pared sería
Igualando las dos expresiones de energía mecánica despejamos el valor máximo de velocidad para que no choque con la pared.







































