Movimiento relativo (G.I.T.I.)

Introducción

Cuando se estudia el movimiento de un único sólido rígido, se tiene la expresión general para el campo de velocidades

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

que nos dice que podemos conocer la velocidad de cada punto conocidos 6 datos: las 3 componentes del vector velocidad angular ${\vec {\omega }}$ y las 3 componentes de la velocidad de un punto arbitrario que tomamos como origen de coordenadas.

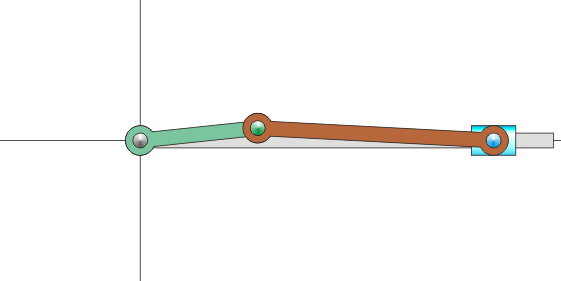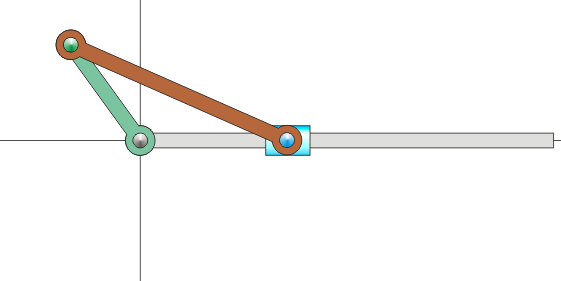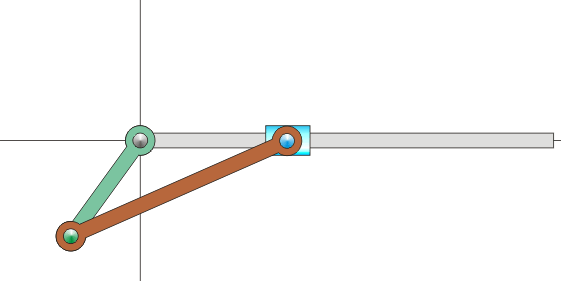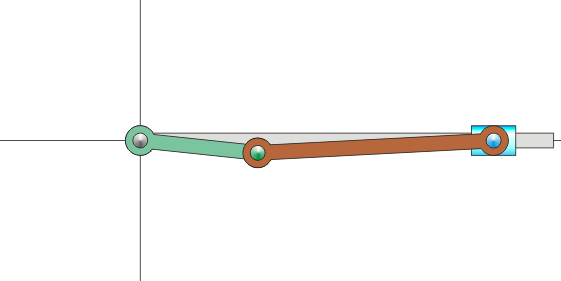
Sin embargo, en muchas situaciones, ni la velocidad angular ni la velocidad de O son datos inmediatos. Por ejemplo, consideremos el mecanismo sencillo de una biela y una manivela, como los que se encuentran dentro de un motor de explosión. Está formado por dos barras. Una, la manivela, gira en torno a uno de sus extremos, unido a un punto fijo. La segunda, la biela, tiene uno de sus extremos articulado al extremo móvil de la manivela, mientras que el otro está obligado a moverse en línea recta.

Es claro que, respecto a un sistema fijo, la manivela efectúa un movimiento de rotación, pero ¿qué movimiento realiza la biela en este mismo sistema? No es evidente de entrada, pues se desplaza a la vez que gira. Lo que sí sabemos es que, vista desde la manivela, la biela está girando respecto a su extremo.

Se trata entonces de hacer una composición de movimientos. El movimiento de la biela lo podemos describir como una rotación en torno a un extremo de la manivela, que a la vez gira en torno a su otro extremo respecto al sistema fijo.

Un ejemplo tridimensional lo representa un cono que rueda sobre un plano. Podemos ver este movimiento como una rotación instantánea en torno a la recta de contacto entre el cono y el plano (pues los puntos de contacto tienen velocidad nula y forman el EIR) pero también puede verse como una composición de dos rotaciones, una en torno a un eje vertical y otra en torno al eje del cono.

En este tema veremos el tratamiento matemático de la descripción de movimientos de sólidos en varios sistemas de referencia simultáneos (movimientos relativos), así como la composición de dos o más movimientos rígidos para dar lugar a un movimiento neto.

Notación y definiciones

Sólidos y sistemas de referencia

El primer paso para estudiar el movimiento relativo consiste en generalizar el concepto de sólido rígido.

Normalmente, cuando uno piensa en un sólido rígido imagina un objeto amorfo, como una piedra, o moldeado, como una pieza de un mecanismo, pero en cualquier caso de tamaño finito. Cuando se habla de los puntos del sólido se piensa en los átomos que lo componen. No tendría sentido considerar punto del sólido a un lugar del espacio en el que no se encuentra el sólido en cuestión.

No obstante, tenemos una fórmula general para las velocidades del punto del sólido, que depende sólo de la posición del punto respecto a un cierto sistema de referencia, no de si en ese punto se encuentra una partícula material o no. Igualmente, la fórmula no requiere que se trate de un verdadero sólido rígido. Un sólido deformable, un líquido o un gas cuyos puntos se muevan según la fórmula anterior describe un movimiento rígido, aunque el medio material no sea indeformable.

Podemos extender entonces el concepto de sólido rígido, abstrayendo de su naturaleza material o finita, a un conjunto de puntos (que abarca todo el espacio) descrito por un cierto sistema de referencia, y tal que el campo de velocidades (y aceleraciones) es el correspondiente a un movimiento rígido

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

Si tenemos varios sólidos, a cada uno de ellos irá asociado un sistema de referencia y una distribución de velocidades para todos los puntos del espacio, independientemente de si forman parte del medio material o no. Es más, en la descripción de un problema aparecen usualmente sólidos intermedios que no poseen existencia material alguna. Usaremos las expresiones "sólido" y "sistema de referencia" de manera sinónima.

Un punto P del espacio no pertenecerá entonces a un sólido en concreto, sino a todos ellos simultáneamente.

Para poder visualizar este concepto podemos volver al ejemplo del mecanismo biela-manivela. El movimiento de este sistema transcurre en un plano, por lo que podemos prescindir de la tercera coordenada. El sistema se compone de tres sólidos: la barra fija (sólido 1), la manivela (sólido 0) y la biela (sólido 2). A cada uno de ellos podemos asociar un sistema de referencia en un plano. Podemos imaginar estos sistemas de referencia como hojas de papel superpuestas. Habrá una hoja de papel pegada a la barra. Sobre ella una hoja de papel unida a la manivela y sobre ésta una tercera hoja unida a la biela. Cada hoja se extiende a todo el plano. En cada instante, cada hoja se mueve respecto a las otras dos, aunque sigan superpuestas.

Un punto P del plano lo podemos imaginar como un alfiler que, en un instante dado, atraviesa simultáneamente las tres hojas de papel, de forma que tenemos un agujero en cada uno de las hojas, por ello decimos que el punto P está en los tres sólidos, aunque tenga vectores de posición diferentes en cada uno.

Cuando los sólidos se mueven unos respecto a los otros, la posición del punto P puede permanecer fija en alguno de los sólidos, pero cambiar en los otros. El punto P tendrá velocidad nula en uno de los sistemas de referencia y distinta de cero en los otros dos. Habrá situaciones, como el punto de articulación de la biela y la manivela, que tendrá velocidad nula en los sólidos 0 y 2, pero que estará en movimiento respecto al sólido 1.

Observemos que podemos hallar el estado de movimiento de, por ejemplo, la articulación de la biela con la barra, considerando esta articulación como parte del sólido 0 (la manivela) pese a que físicamente este punto no forme parte de la manivela. Debemos imaginarnos unos ejes solidarios con la manivela que llegan hasta este punto y determinar cómo se mueve un punto fijo en este sistema de referencia cuando la manivela efectúa sus movimiento de rotación respecto a la barra (o respecto a la biela).

En un sistema tridimensional la idea es exactamente la misma, aunque en lugar de hojas de papel superpuestas deberíamos imaginar volúmenes coincidentes que se mueven de distinta manera. Dado que esta idea es difícil de concebir, nos conformaremos con dibujar sistemas de ejes en movimiento relativo, pero manteniendo siempre en mente que los sólidos no son solo los ejes, sino todo el espacio.

Según esto, la pregunta ¿cuál es la velocidad del punto P? no tiene sentido. La pregunta siempre debe ser ¿cuál es la velocidad del punto P, considerado como parte del sólido i, respecto al sólido k?

Notación

Emplearemos la siguiente notación:

{ik}

movimiento del sólido i respecto al sólido k

${\vec {r}}_{ik}^{P}$

Posición de un punto P, considerado como parte del sólido i, respecto a un sistema de referencia ligado al sólido k. Nótese que en principio el primer subíndice parecería supérfluo, pues hemos dicho que un punto pertenece a todos los sólidos simultáneamente. Pero, cuando seguimos la evolución temporal de un punto material en concreto sí se hace importante saber a qué sólido pertenece, pues la trayectoria dependerá del sólido del que forme parte.

${\vec {v}}_{ik}^{P}$

Velocidad de un punto P del sólido i respecto a un sistema ligado al sólido k.

${\vec {a}}_{ik}^{P}$

Aceleración de un punto P del sólido i respecto a un sistema ligado al sólido k.

${\vec {\omega }}_{ik}$

Velocidad angular del sólido i respecto al sólido k. Esta velocidad angular no lleva superíndice pues no está asociada a ningún punto en concreto, sino que es un vector libre, válido para todo el sólido.

${\vec {\alpha }}_{ik}$

Aceleración angular del sólido i respecto al sólido k.

El subíndice en las derivadas quiere decir que se deriva considerando que los ejes del sistema k permanecen fijos.

En el caso en que hay solo tres sólidos, son típicas los siguientes términos

Sólido de referencia o fijo

El etiquetado como 1. Nótese que esto no implica que este sólido se encuentre en un estado de reposo absoluto, inexistente, o siquiera que sea un sistema de referencia inercial.

Sólido problema

El etiquetado como 2.

Sólido intermedio

El etiquetado como 0.

Movimiento absoluto

El del sólido problema respecto al de referencia o fijo: {21}

Movimiento relativo

El del sólido problema respecto al sólido intermedio: {20}

Movimiento de arrastre

El del sólido intermedio respecto al de referencia: {01}

Sistemas de ejes

Cada sólido de un sistema lleva asociado un sistema de ejes coordenados. El sistema ligado al sólido $n$ se identificará por la presencia de un origen de coordenadas $O_{n}$ y un conjunto de ejes ortogonales $O_{n}X_{n}$, $O_{n}Y_{n}$ y $O_{n}Z_{n}$.

Dados los tres ejes, existirá una base ortonormal ligada al sólido $n$, $\{{\vec {\imath }}_{n},{\vec {\jmath }}_{n},{\vec {k}}_{n}\}$, formada por los vectores unitarios en la dirección de los ejes.

Esto quiere decir que un determinado vector (por ejemplo, la velocidad de un punto en concreto), podrá tener diferentes componentes, en el mismo instante, según el sólido al que lo estemos refiriendo, ya que la base vectorial será diferente de un sólido a otro.

Dado que la elección de ejes es arbitraria, cuando se estudia el estado de movimiento instantáneo de un sólido, a menudo podrán elegirse sistemas de ejes coincidentes instantáneamente, de manera que en ese momento las bases vectoriales son idénticas y las componentes de un vector son las mismas para todos los sólidos. Esta igualdad, no obstante, será solo momentánea, ya que debido al movimiento relativo, ejes y bases se habrán separado al instante siguiente. Esto es especialmente relevante a la hora de calcular derivadas respecto al tiempo.

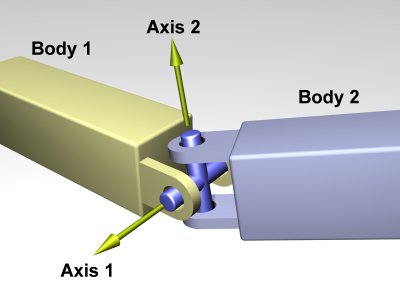
Sólidos vinculados. Pares cinemáticos

El movimiento de un sólido respecto a otro puede estar limitado por la presencia de vínculos o ligaduras. Por ejemplo, en una articulación como la de la biela y la manivela, el punto de la articulación pertenece permanentemente a ambos sólidos, lo que reduce el número de grados de libertad y limita el espectro de movimientos posibles.

Cuando tenemos dos sólidos vinculados se dice que tenemos un par cinemático. Si lo que tenemos es una sucesión de sólidos vinculados, por ejemplo en un brazo robótico con varias articulaciones, se dice que tenemos una cadena de sólidos.

Los dos sólidos que forman un par cinemático pueden considerarse como sólidos independientes, modelando el vínculo por una ecuación que limita los valores posibles de las velocidades y aceleraciones de los puntos de contacto o del sólido completo.

La existencia de pares cinemáticos conocidos aconseja reducir el movimiento relativo {21} en el punto donde se encuentra el vínculo. De esta forma puede eliminarse componentes de la velocidad ${\vec {v}}_{21}^{O}$ o de la velocidad angular ${\vec {\omega }}_{21}$, simplificando las expresiones y permitiendo la identificación del movimiento relativo, mediante su reducción canónica.

Clasificación

Par cilíndrico (corredera cilíndrica)

El sólido 2 está obligado a girar en torno a un cierto eje, sobre el cual puede haber una cierta velocidad de deslizamiento. Si hacemos que este eje sea OZ y A un punto del eje se verifica

${\vec {\omega }}_{21}=\omega _{21}{\vec {k}}$    ${\vec {v}}_{21}^{A}=v_{d}{\vec {k}}$

En principio las dos magnitudes poseen valores independientes y arbitrarios (dos grados de libertad relativa). El movimiento {21} es un movimiento helicoidal con EIRMD el que apunta en la dirección fijada por el vínculo. Ocasionalmente, puede resultar una rotación pura, cuando $v_{d}=0$.

Par helicoidal (tornillo)

Como en el anterior, el sólido 2 gira en torno a un eje dado, sobre el cual se desliza, pero la velocidad de deslizamiento no es arbitraria, sino que está condicionada por el paso de rosca, $b$, que es la distancia que avanza cuando gira una vuelta completa. Sólo existe pues un grado de libertad relativo. Esto se modela como

${\vec {\omega }}_{21}=\omega _{21}{\vec {k}}$    ${\vec {v}}_{21}^{A}={\frac {\omega _{21}b}{2\pi }}{\vec {k}}$

De nuevo el movimiento relativo es uno helicoidal, con EIRMD el del tornillo. En este caso, al existir una relación entre ambas velocidades, el movimiento no puede reducirse a una rotación.

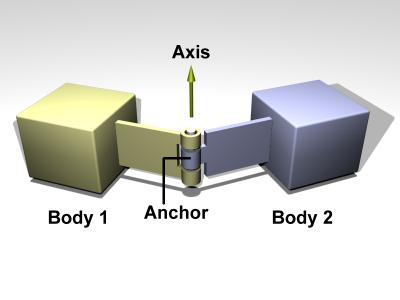
Par de revolución (bisagra)

De nuevo el eje de giro está fijado, pero ahora la velocidad de deslizamiento es nula.

${\vec {\omega }}_{21}=\omega _{21}{\vec {k}}$    ${\vec {v}}_{21}^{A}={\vec {0}}$

Es un caso particular del par helicoidal, haciendo $b=0$. Hay un grado de libertad relativa. Este par cinemático es el que se aplica a una rueda respecto a un eje en el que está ensartada. El movimiento relativo {21} es una rotación pura con EIR el fijado por el vínculo.

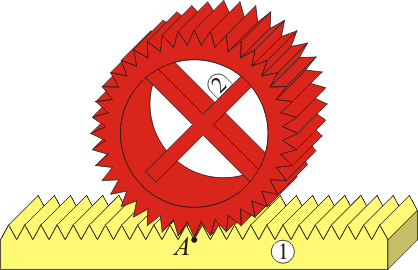
Par de revolución instantáneo (engranaje)

El punto de contacto entre los sólidos se encuentra instantáneamente en reposo, y el sólido 2 sólo puede rotar en torno a un cierto eje.

${\vec {\omega }}_{21}=\omega _{21}{\vec {k}}$    ${\vec {v}}_{21}^{A}={\vec {0}}$

El movimiento relativo es una rotación en torno a un EIR que pasa por A y que tiene la dirección permitida por el vínculo. Este vínculo incluye también el movimiento de una rueda respecto al suelo, cuando dicha rueda no puede desplazarse lateralmente, sino solo en una dirección.

Par prismático (corredera rectangular)

El sólido 2 puede deslizarse a lo largo de un cierto eje, pero no puede girar en torno a él (un único grado de libertad relativa)

${\vec {\omega }}_{21}={\vec {0}}$    ${\vec {v}}_{21}^{A}=v_{d}{\vec {k}}$

El movimiento relativo en este caso es una traslación, siendo la velocidad de todos los puntos en la dirección fijada por el vínculo.

Par esférico (rótula o articulación)

El punto A (centro de la rótula) es un punto fijo en el movimiento relativo de los dos sólidos. El sólido 2 puede girar libremente (pero no trasladarse) respecto al 1. Por ello

${\vec {\omega }}_{21}\neq {\vec {0}}$    ${\vec {v}}_{21}^{A}={\vec {0}}$

El movimiento relativo del sólido 2 respecto al 1 es siempre una rotación pura en torno a un eje que pasa por A. Existen tres grados de libertad relativa rotacionales.

Par esférico instantáneo (rodadura y pivotamiento)

El punto de contacto entre los sólidos se encuentra en reposo instantáneo, pudiendo el sólido 2 rotar alrededor de cualquier eje que pase por el punto de contacto.

${\vec {\omega }}_{21}\neq {\vec {0}}$    ${\vec {v}}_{21}^{A}={\vec {0}}$

El movimiento es de nuevo una rotación pura en torno a un eje que pasa por el punto A.

Par rígido (empotramiento, voladizo o cantilever)

Los dos sólidos forman en realidad uno solo, ya que en el punto de contacto la unión es rígida

${\vec {\omega }}_{21}={\vec {0}}$    ${\vec {v}}_{21}^{A}={\vec {0}}$

El sólido 2 se encuentra en reposo respecto al 1 (cero grados de libertad relativa).

Pares Cinemáticos

Cilíndrico	Helicoidal
De revolución	De revolución instantáneo
Prismático	Esférico
Esférico instantáneo	Rígido

Estos pares pueden combinarse entre sí, aumentando (o reduciendo en su caso) el número de grados de libertad relativos. Así, por ejemplo, una junta cardán o junta universal combina dos pares de revolución, permitiendo orientaciones arbitrarias del sólido 2 respecto al 1. Por ello, es común en todo tipo de brazos articulados. En este sentido se asemeja a una rótula, con la diferencia de que no permite la rotación en torno a uno de los tres ejes posibles.

Deslizamiento, rodadura y pivotamiento

Cuando tenemos dos sólidos en contacto, tales que un punto del sólido 2 se encuentra sobre una superficie del sólido 1 (por ejemplo, una pelota sobre una mesa), es posible que el punto de contacto esté en reposo relativo (como en el par esférico instantáneo o el de revolución instantáneo), o que no lo esté. Cuando el punto de contacto posee una cierta velocidad se dice que existe deslizamiento entre los sólidos. Se define la velocidad de deslizamiento entre los sólidos como la del punto de contacto, ${\vec {v}}_{21}^{A}$

Esta velocidad será necesariamente tangente a la superficie y por tanto ortogonal a ${\vec {n}}$, el vector normal a la superficie.

${\vec {v}}_{21}^{A}\cdot {\vec {n}}=0$

Por otra parte, la velocidad angular puede tener una parte en la dirección perpendicular a la superficie, esto es, el sólido 2 posee un giro en torno a un eje perpendicular a la superficie Y paralelo, por tanto, al vector ${\vec {n}}$). Cuando esto ocurre se dice que el sólido 2 pivota sobre el uno y esta componente de la velocidad angular se denomina velocidad angular de pivotamiento.

${\vec {\omega }}_{p}={\vec {\omega }}_{\parallel }=({\vec {\omega }}_{21}\cdot {\vec {n}}){\vec {n}}$

Además de la posible parte perpendicular a la superficie, la velocidad angular posee una parte tangente a la superficie (y perpendicular a ${\vec {n}}$, por tanto), de forma que el sólido 2 posee una componente de giro a en torno a un eje paralelo a la superficie. Se dice entonces que tenemos rodadura en el punto de contacto, siendo la velocidad angular de rodadura

${\vec {\omega }}_{r}={\vec {\omega }}_{\perp }={\vec {n}}\times ({\vec {\omega }}_{21}\times {\vec {n}})$

En un movimiento general tendremos las tres componentes: rodadura, deslizamiento y pivotamiento, siendo la velocidad de cualquier punto del sólido 2

${\vec {v}}_{21}^{P}={\vec {v}}_{21}^{A}+{\vec {\omega }}_{21}\times {\overrightarrow {AP}}$

No obstante, en muchas ocasiones algunas de estas componentes son nulas. Así, tenemos los casos:

Rodar y pivotar sin deslizar

La velocidad de deslizamiento es nula

${\vec {v}}_{21}^{A}={\vec {0}}$

El movimiento instantáneo del sólido 2 es una rotación pura en torno a un cierto eje que pasa por el punto de contacto. Este es el movimiento que describe habitualmente, por ejemplo, una bola que se mueve sobre una superficie horizontal con rozamiento.

Rodar sin deslizar

Si no se indica que existe pivotamiento, se supone que este es nulo, en este caso, la velocidad angular ${\vec {\omega }}_{21}$ es tangente a la superficie del sólido 1. El movimiento relativo es una rotación pura alrededor de un eje tangente a la superficie de 1. Este es el movimiento de un disco que rueda sobre un plano. Así, respecto al suelo, una rueda de un coche no rueda en torno a su eje, sino en torno a un eje que pasa por el punto donde toca el suelo y es tangente a este.

Deslizamiento sin rodadura

La velocidad angular es nula (se supone que tampoco hay pivotamiento) y el sólido 2 se traslada respecto al 1 con la velocidad

${\vec {v}}_{21}^{P}={\vec {v}}_{21}^{A}$

Esto ocurre, por ejemplo, cuando se arrastra un cierto sólido (una caja, por ejemplo) sobre otro.

Estas situaciones pueden venir obligadas por los pares cinemáticos. Así un par de deslizamiento implica deslizamiento sin rodadura ni pivotamiento; un par esférico, rodadura y pivotamiento sin deslizamiento; un par de revolución, rodadura sin deslizamiento ni pivotamiento; etc.

Deslizamiento	Rodadura	Pivotamiento

Derivación en ejes móviles. Fórmulas de Poisson

El que la velocidad de un punto pueda ser cero en un sistema de referencia y no nula en otro muestra que la derivada respecto al tiempo depende del sistema de referencia, que debe ser indicado explícitamente.

Este problema no aparece con las derivadas de las cantidades escalares, cuyo valor es el mismo para todos los sistemas de referencia. La cuestión surge con las magnitudes vectoriales (y tensoriales, que no consideraremos) debido a que los propios vectores de la base son funciones del tiempo, al moverse un sistema de referencia respecto a otro.

Derivada temporal en una base

Definimos la derivada temporal de una magnitud vectorial ${\vec {A}}(t)$ en un sistema 1, como la que se obtiene, aplicando las reglas habituales de derivación, admitiendo que los vectores de la base asociada a dicho sistema permanecen constantes, esto es, si

${\vec {A}}=A_{x}{\vec {\imath }}_{1}+A_{y}{\vec {\jmath }}_{1}+A_{z}{\vec {k}}_{1}$

su derivada temporal en el sistema 1 es

$\left.{\frac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{1}={\frac {\mathrm {d} A_{x}}{\mathrm {d} t}}{\vec {\imath }}_{1}+{\frac {\mathrm {d} A_{y}}{\mathrm {d} t}}{\vec {\jmath }}_{1}+{\frac {\mathrm {d} A_{y}}{\mathrm {d} t}}{\vec {k}}_{1}$

Nótese que las derivadas de las componentes, que son cantidades escalares, no precisan subíndice.

La posición y las velocidades y aceleraciones definidas en la sección anterior son, en principio, magnitudes instantáneas, esto es, nos informan de la posición, velocidad y aceleración de un punto en concreto, o de todos los puntos de un sólido en un instante dado. Como tales no son, en principio, derivables respecto al tiempo (ya que una derivada implica una diferencia entre los valores en dos instantes diferentes).

No obstante lo anterior, cuando se estudia un movimiento relativo de un sólido respecto a otro a lo largo del tiempo, en ocasiones es posible determinar la posición de un punto material concreto como función del tiempo, ${\vec {r}}_{21}^{P}={\vec {r}}_{21}^{P}(t)$. En ese caso sí podemos calcular sus derivadas. Definimos la velocidad y la aceleración de un punto P (que tomamos como perteneciente al sólido 2, aunque puede tratarse de una simple partícula material), tal como se miden en el sistema 1 como

${\vec {v}}_{21}^{P}=\left.{\frac {\mathrm {d} {\vec {r}}_{21}^{P}}{\mathrm {d} t}}\right|_{1}$    ${\vec {a}}_{21}^{P}=\left.{\frac {\mathrm {d} {\vec {v}}_{21}^{P}}{\mathrm {d} t}}\right|_{1}$

Asimismo, el movimiento relativo de un sólido respecto a otro viene caracterizado además de por la velocidad y aceleración de un punto material concreto, por la velocidad y aceleración angulares, cumpliéndose

${\vec {\alpha }}_{21}=\left.{\frac {\mathrm {d} {\vec {\omega }}_{21}}{\mathrm {d} t}}\right|_{1}$

Relación entre derivadas temporales

Supongamos que tenemos una cierta cantidad vectorial ${\vec {A}}(t)$ de la que hemos calculado, en un instante $t_{0}$, su derivada temporal en dos sistemas de referencia 0 y 1, y queremos relacionar estas dos cantidades. Cualquier vector tendrá una cierta expresión en cada una de las bases vectoriales correspondientes a los diferentes sólidos.

Partimos de la expresión en la base ligada al sólido “0”

${\vec {A}}=A_{x}{\vec {\imath }}_{0}+A_{y}{\vec {\jmath }}_{0}+A_{z}{\vec {k}}_{0}$

Si derivamos ${\vec {A}}$ respecto al tiempo en el sistema 1

$\left.{\frac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{1}={\frac {\mathrm {d} A_{x}}{\mathrm {d} t}}{\vec {\imath }}_{0}+A_{x}\left.{\frac {\mathrm {d} {\vec {\imath }}_{0}}{\mathrm {d} t}}\right|_{1}+{\frac {\mathrm {d} A_{y}}{\mathrm {d} t}}{\vec {\jmath }}_{0}+A_{y}\left.{\frac {\mathrm {d} {\vec {\jmath }}_{0}}{\mathrm {d} t}}\right|_{1}+{\frac {\mathrm {d} A_{z}}{\mathrm {d} t}}{\vec {k}}_{0}+A_{z}\left.{\frac {\mathrm {d} {\vec {k}}_{0}}{\mathrm {d} t}}\right|_{1}$

Necesitamos entonces conocer la derivada temporal de los vectores de la base. El vector unitario ${\vec {\imath }}_{0}$ es el que une al origen de coordenadas, O, con un punto A, situado a una distancia unidad a lo largo del eje $X_{0}$. Su derivada es

$\left.{\frac {\mathrm {d} {\vec {\imath }}_{0}}{\mathrm {d} t}}\right|_{1}=\left.{\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\vec {r}}_{01}^{A}-{\vec {r}}_{01}^{O}\right)\right|_{1}={\vec {v}}_{01}^{A}-{\vec {v}}_{01}^{O}$

Aplicando la expresión del campo de velocidades de un sólido

${\vec {v}}_{01}^{A}={\vec {v}}_{01}^{O}+{\vec {\omega }}_{01}\times {\overrightarrow {OA}}={\vec {v}}_{01}^{O}+{\vec {\omega }}_{01}\times {\vec {\imath }}_{0}$

llegamos a

$\left.{\frac {\mathrm {d} {\vec {\imath }}_{0}}{\mathrm {d} t}}\right|_{1}={\vec {\omega }}_{01}\times {\vec {\imath }}_{0}$

A este mismo resultado se llega directamente empleando la equiproyectividad del campo de velocidades y es justamente la propiedad que permite definir la velocidad angular del sólido, de acuerdo con la demostración del Teorema de Chasles.

Análogamente tenemos, para los otros dos vectores

$\left.{\frac {\mathrm {d} {\vec {\jmath }}_{0}}{\mathrm {d} t}}\right|_{1}={\vec {\omega }}_{01}\times {\vec {\jmath }}_{0}$     $\left.{\frac {\mathrm {d} {\vec {k}}_{0}}{\mathrm {d} t}}\right|_{1}={\vec {\omega }}_{01}\times {\vec {k}}_{0}$

Estas tres igualdades se conocen como fórmulas de Poisson.

Sustituyendo y reordenando términos nos queda

$\left.{\frac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{1}={\frac {\mathrm {d} A_{x}}{\mathrm {d} t}}{\vec {\imath }}_{0}+{\frac {\mathrm {d} A_{y}}{\mathrm {d} t}}{\vec {\jmath }}_{0}+{\frac {\mathrm {d} A_{y}}{\mathrm {d} t}}{\vec {k}}_{0}+{\vec {\omega }}_{01}\times \left(A_{x}{\vec {\imath }}_{0}+A_{y}{\vec {\jmath }}_{0}+A_{z}{\vec {k}}_{0}\right)$

que equivale a

$\left.{\frac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{1}=\left.{\frac {\mathrm {d} {\vec {A}}}{\mathrm {d} t}}\right|_{0}+{\vec {\omega }}_{01}\times {\vec {A}}$

Esta igualdad también se conoce como fórmula de Poisson y contiene como casos particulares a las expresiones correspondientes a los vectores de la base.

Esta identidad es aplicable a cualquier magnitud vectorial, lo que incluye a las posiciones, velocidades y las propias velocidades angulares.

Composición de dos movimientos

Composición de velocidades

Una vez que disponemos de la fórmula de Poisson, podemos aplicarla para relacionar la velocidad de un punto, medida por dos observadores diferentes.

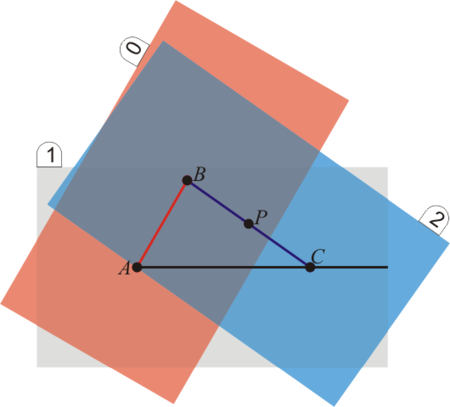
Supongamos un punto P, que se mueve con el sólido móvil 2, tal que su vector de posición respecto al origen $O_{1}$ de un sistema fijo 1 es

${\vec {r}}_{21}^{P}={\overrightarrow {O_{1}P}}$

y respecto al origen O de un sólido intermedio 0 es

${\vec {r}}_{20}^{P}={\overrightarrow {OP}}$

Estos dos vectores se relacionan por

${\overrightarrow {O_{1}P}}={\overrightarrow {O_{1}O}}+{\overrightarrow {OP}}$ ⇒ ${\vec {r}}_{21}^{P}={\vec {r}}_{01}^{O}+{\vec {r}}_{20}^{P}$

Derivando aquí respecto al tiempo en el sistema 1 llegamos a la relación

${\vec {v}}_{21}^{P}=\left.{\frac {\mathrm {d} {\vec {r}}_{21}^{P}}{\mathrm {d} t}}\right|_{1}=\left.{\frac {\mathrm {d} {\vec {r}}_{01}^{O}}{\mathrm {d} t}}\right|_{1}+\left.{\frac {\mathrm {d} {\vec {r}}_{20}^{P}}{\mathrm {d} t}}\right|_{1}$

El primero de los dos términos es la velocidad del punto O, medida en el sistema 1.

$\left.{\frac {\mathrm {d} {\vec {r}}_{01}^{O}}{\mathrm {d} t}}\right|_{1}={\vec {v}}_{01}^{O}$

Para el segundo, relacionamos esta derivada con la medida en el sólido 0

$\left.{\frac {\mathrm {d} {\vec {r}}_{20}^{P}}{\mathrm {d} t}}\right|_{1}=\left.{\frac {\mathrm {d} {\vec {r}}_{20}^{P}}{\mathrm {d} t}}\right|_{0}+{\vec {\omega }}_{01}\times {\vec {r}}_{20}^{P}={\vec {v}}_{20}^{P}+{\vec {\omega }}_{01}\times {\overrightarrow {OP}}$

Sumando las dos contribuciones

${\vec {v}}_{21}^{P}={\vec {v}}_{20}^{P}+{\vec {v}}_{01}^{O}+{\vec {\omega }}_{01}\times {\overrightarrow {OP}}$

Si aquí sustituimos el campo de velocidades del sólido 0, la velocidad se reduce a

${\vec {v}}_{21}^{P}={\vec {v}}_{20}^{P}+{\vec {v}}_{01}^{P}$

esto es: la velocidad del punto P del sólido móvil, medida por un observador ligado al sólido “1” (que tomamos como fijo o de referencia) es la suma de la medida por uno ligado al sólido intermedio “0” más la que tendría el punto P, si perteneciera al sólido intermedio “0”, medida en el sistema fijo.

Este resultado es aplicable a cualquier terna de sólidos. En general

${\vec {v}}_{ik}^{P}={\vec {v}}_{in}^{P}+{\vec {v}}_{nk}^{P}$

No hay nada de especial que convierta a 0 en el sólido intermedio y a 1 en fijo; del mismo modo tenemos

${\vec {v}}_{20}^{P}={\vec {v}}_{21}^{P}+{\vec {v}}_{10}^{P}$

donde se han intercambiado sus papeles. Comparando esta expresión con la anterior obtenemos que

${\vec {v}}_{01}^{P}=-{\vec {v}}_{10}^{P}$

Hay que destacar que la expresión de la velocidad como suma de velocidades es una relación entre valores instantáneos de las diferentes cantidades, no como funciones del tiempo. Por tanto, no puede derivarse respecto al tiempo para hallar las aceleraciones. La razón es la siguiente: en la expresión aparece la velocidad del punto P del sólido 0, pero el punto P no es siempre el mismo punto material en el sólido 0, sino aquel que en cada instante coincide con el punto P del sólido 2 (que sí es un punto material), esto quiere decir que en el instante $t$ empleamos la velocidad de un punto P, pero en el instante $t+dt$ empleamos la velocidad de otro punto P diferente, y la diferencia de estas dos velocidades no da la aceleración de ninguno de los dos.

    

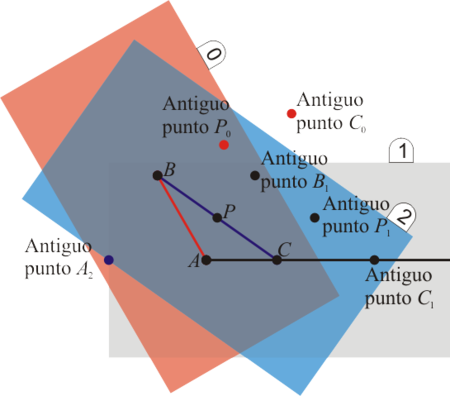
La expresión en términos de la velocidad de O y la velocidad angular, en cambio, si puede derivarse respecto al tiempo, ya que el punto O del sólido 0 si está perfectamente definido y se puede seguir su movimiento en el tiempo.

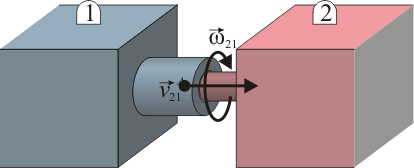
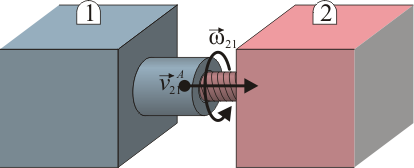
Una consecuencia de la ecuación anterior, y que parece ir contra el sentido común, es la siguiente. Supongamos que tenemos dos observadores A y B, pertenecientes a sólidos 1 y 2, respectivamente. En general, no se cumple que la velocidad de A medida por B sea opuesta a la de B medida por A

${\vec {v}}_{12}^{A}\neq -{\vec {v}}_{21}^{B}$

En este problema se analiza un ejemplo que muestra distintas variantes de esta desigualdad.

Composición de velocidades angulares

Una vez que tenemos la relación entre velocidades lineales, podemos hallar la de velocidades angulares.

Partimos de la ley de composición de velocidades. Tenemos que, en un instante dado, y para cualquier punto P

${\vec {v}}_{21}^{P}={\vec {v}}_{20}^{P}+{\vec {v}}_{01}^{P}$

Restando esta expresión de la correspondiente a otro punto O nos queda la relación entre velocidades relativas

$\left({\vec {v}}_{21}^{P}-{\vec {v}}_{21}^{O}\right)=\left({\vec {v}}_{20}^{P}-{\vec {v}}_{20}^{O}\right)+\left({\vec {v}}_{01}^{P}-{\vec {v}}_{01}^{O}\right)$

En esta expresión los tres movimientos son rígidos, por lo que verifican

${\vec {v}}_{ik}^{P}={\vec {v}}_{ik}^{O}+{\vec {\omega }}_{ik}\times {\overrightarrow {OP}}$

lo que nos da la relación

${\vec {\omega }}_{21}\times {\overrightarrow {OP}}={\vec {\omega }}_{20}\times {\overrightarrow {OP}}+{\vec {\omega }}_{01}\times {\overrightarrow {OP}}$

Puesto que esta relación debe cumplirse para todos los pares de puntos, la única posibilidad es que

${\vec {\omega }}_{21}={\vec {\omega }}_{20}+{\vec {\omega }}_{01}$

A diferencia de la ecuación para las velocidades, esta relación sí puede derivarse respecto al tiempo. La razón es que la velocidad angular es un invariante, no depende de la posición de ningún punto en concreto, por lo que desaparece el problema de si el punto P en cada instante es el mismo o no.

Composición de aceleraciones. Teorema de Coriolis

Podemos relacionar las aceleraciones medidas por dos observadores a partir de la expresión

${\vec {v}}_{21}^{P}={\vec {v}}_{20}^{P}+{\vec {v}}_{01}^{O}+{\vec {\omega }}_{01}\times {\overrightarrow {OP}}$

Derivando respecto al tiempo en el sistema 1 obtenemos, para cada uno de los términos

${\begin{array}{rcl}\displaystyle \left.{\frac {\mathrm {d} {\vec {v}}_{21}^{P}}{\mathrm {d} t}}\right|_{1}&=&{\vec {a}}_{21}^{P}\\&&\\\displaystyle \left.{\frac {\mathrm {d} {\vec {v}}_{20}^{P}}{\mathrm {d} t}}\right|_{1}&=&\displaystyle \left.{\frac {\mathrm {d} {\vec {v}}_{20}^{P}}{\mathrm {d} t}}\right|_{0}+{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{P}={\vec {a}}_{20}^{P}+{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{P}\\&&\\\displaystyle \left.{\frac {\mathrm {d} {\vec {v}}_{01}^{O}}{\mathrm {d} t}}\right|_{1}&=&{\vec {a}}_{01}^{O}\\&&\\\displaystyle \left.{\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\vec {\omega }}_{01}\times {\overrightarrow {OP}}\right)\right|_{1}&=&\displaystyle \left.{\frac {\mathrm {d} {\vec {\omega }}_{01}}{\mathrm {d} t}}\right|_{1}\times {\overrightarrow {OP}}+{\vec {\omega }}_{01}\times \left.{\frac {\mathrm {d} {\overrightarrow {OP}}}{\mathrm {d} t}}\right|_{1}\\&&\\\displaystyle \left.{\frac {\mathrm {d} {\vec {\omega }}_{01}}{\mathrm {d} t}}\right|_{1}&=&{\vec {\alpha }}_{01}\\&&\\\displaystyle \left.{\frac {\mathrm {d} {\overrightarrow {OP}}}{\mathrm {d} t}}\right|_{1}&=&\displaystyle \left.{\frac {\mathrm {d} {\overrightarrow {OP}}}{\mathrm {d} t}}\right|_{0}+{\vec {\omega }}_{01}\times {\overrightarrow {OP}}={\vec {v}}_{20}^{P}+{\vec {\omega }}_{01}\times {\overrightarrow {OP}}\end{array}}$

Sustituyendo todo esto obtenemos

${\vec {a}}_{21}^{P}={\vec {a}}_{20}^{P}+{\vec {a}}_{01}^{O}+{\vec {\alpha }}_{01}\times {\overrightarrow {OP}}+{\vec {\omega }}_{01}\times ({\vec {\omega }}_{01}\times {\overrightarrow {OP}})+2{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{P}$

Agrupando términos con ayuda de la expresión del campo de aceleraciones de un sólido obtenemos finalmente

${\vec {a}}_{21}^{P}={\vec {a}}_{20}^{P}+{\vec {a}}_{01}^{P}+2{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{P}$

Este es el conocido como Teorema de Coriolis. Vemos que, a diferencia de la velocidad, la aceleración del movimiento absoluto no es la suma de la del movimiento relativo más la del de arrastre.

En el caso particular de que el sólido 2 y el 1 sean el mismo obtenemos

${\vec {0}}={\vec {a}}_{10}^{P}+{\vec {a}}_{01}^{P}+2{\vec {\omega }}_{01}\times {\vec {v}}_{10}^{P}$ ⇒  ${\vec {a}}_{10}^{P}=-{\vec {a}}_{01}^{P}-2{\vec {\omega }}_{01}\times {\vec {v}}_{10}^{P}=-{\vec {a}}_{01}^{P}+2{\vec {\omega }}_{01}\times {\vec {v}}_{01}^{P}\neq -{\vec {a}}_{01}^{P}$

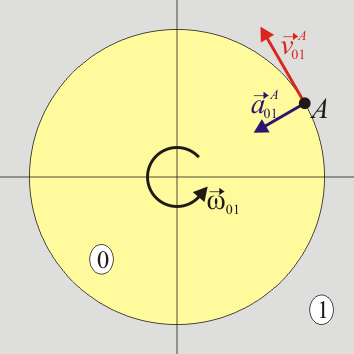
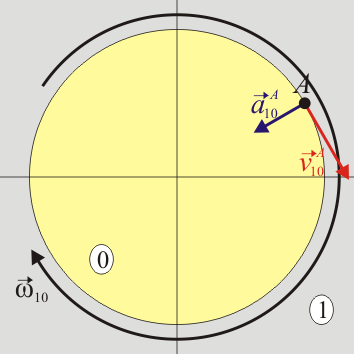
Podemos ilustrar el que no resulten aceleraciones iguales y opuestas con un ejemplo sencilo. Consideremos una plataforma “0” que gira con velocidad angular constante respecto al suelo, considerado como sólido “1”. Sea un punto A de la plataforma. Para un observador situado en el suelo “1”, este punto A está describiendo un movimiento circular uniforme en torno al eje de la plataforma. Por tanto su aceleración, ${\vec {a}}_{01}^{A}$ será radial y hacia adentro.

Desde el suelo	Desde la plataforma

Desde el punto de vista del sólido “0”, en cambio, es el suelo el que gira con velocidad angular constante en sentido contrario. Para este observador un punto A del suelo también está describiendo un movimiento circular uniforme. Por tanto, la aceleración de este punto A del suelo, ${\vec {a}}_{10}^{A}$, también será radial y hacia adentro. Esto es, que para este caso concreto

${\vec {a}}_{10}^{A}={\vec {a}}_{01}^{A}$

Resulta una velocidad igual en módulo y opuesta, una velocidad angular igual en módulo y opuesta, pero una aceleración que no es igual en módulo y opuesta, sino igual a secas. En la fórmula de composición de aceleraciones, el término de Coriolis en este caso es exactamente igual en módulo al doble del primer sumando y con sentido opuesto

${\vec {a}}_{10}^{A}=-{\vec {a}}_{01}^{A}+2{\vec {\omega }}_{01}\times {\vec {v}}_{01}^{P}=-{\vec {a}}_{01}^{A}+2{\vec {a}}_{01}^{A}={\vec {a}}_{01}^{A}$

Composición de aceleraciones angulares

La ley para la composición de aceleraciones angulares la obtenemos derivando la ley de composición de velocidades angulares

${\vec {\omega }}_{21}={\vec {\omega }}_{20}+{\vec {\omega }}_{01}$

Derivando cada término resulta

Derivada de la velocidad angular absoluta

$\left.{\frac {\mathrm {d} {\vec {\omega }}_{21}}{\mathrm {d} t}}\right|_{1}={\vec {\alpha }}_{21}$

Derivada de la velocidad angular relativa

$\left.{\frac {\mathrm {d} {\vec {\omega }}_{20}}{\mathrm {d} t}}\right|_{1}=\left.{\frac {\mathrm {d} {\vec {\omega }}_{20}}{\mathrm {d} t}}\right|_{0}+{\vec {\omega }}_{01}\times {\vec {\omega }}_{20}={\vec {\alpha }}_{20}+{\vec {\omega }}_{01}\times {\vec {\omega }}_{20}$

Derivada de la velocidad angular de arrastre

$\left.{\frac {\mathrm {d} {\vec {\omega }}_{01}}{\mathrm {d} t}}\right|_{1}={\vec {\alpha }}_{01}$

Combinando todos estos términos:

${\vec {\alpha }}_{21}={\vec {\alpha }}_{20}+{\vec {\alpha }}_{01}+{\vec {\omega }}_{01}\times {\vec {\omega }}_{20}$

En el caso particular de que el sólido 2 y el 1 sean el mismo nos queda

${\vec {0}}={\vec {\alpha }}_{10}+{\vec {\alpha }}_{01}+\overbrace {{\vec {\omega }}_{01}\times {\vec {\omega }}_{10}} ^{={\vec {0}}}\qquad \Rightarrow \qquad {\vec {\alpha }}_{10}=-{\vec {\alpha }}_{01}$

esto es, la aceleración angular sí es antisimétrica, a diferencia de lo que ocurre con la aceleración lineal.

Composición general de movimientos. Composiciones equivalentes

Generalización de las fórmulas

Las fórmulas de composición de velocidades pueden extenderse a cualquier terna de sólidos, de manera que tenemos las relaciones para la velocidad angular

${\vec {\omega }}_{ik}={\vec {\omega }}_{ij}+{\vec {\omega }}_{jk}$

y para la velocidad lineal instantánea de un punto O

${\vec {v}}_{ik}^{\,O}={\vec {v}}_{ij}^{\,O}+{\vec {v}}_{jk}^{\,O}$

Si en vez de tres sólidos tenemos una cadena de sólidos 1,2,...,n, por ejemplo, en un brazo articulado con diferentes tramos compuesta por cuatro o más sólidos y lo que nos interesa es el movimiento absoluto final del sólido n respecto al sólido 1, su velocidad angular será la suma de las de los diferentes movimientos relativos

${\vec {\omega }}_{n1}={\vec {\omega }}_{n(n-1)}+\cdots +{\vec {\omega }}_{21}=\sum _{i=1}^{n-1}{\vec {\omega }}_{(i+1)i}$

y la velocidad lineal de un punto O,

${\vec {v}}_{n1}^{\,O}={\vec {v}}_{n(n-1)}^{\,O}+\cdots +{\vec {v}}_{21}^{\,O}=\sum _{i=1}^{n-1}{\vec {v}}_{(i+1)i}^{\,O}$

La velocidad de cualquier otro punto puede hallarse bien empleando esta misma fórmula, esto es, hallando la velocidad de P en cada uno de los movimientos relativos y luego sumando los resultados, o bien empleando la expresión del campo de velocidades de un sólido

${\vec {v}}_{n1}^{\,P}={\vec {v}}_{n1}^{\,O}+{\vec {\omega }}_{n1}\times {\overrightarrow {OP}}$

En particular, si los movimientos relativos son todos rotaciones puras y los puntos $O_{1}$, $O_{2}$,... son puntos de los sucesivos ejes instantáneos de rotación, la velocidad lineal del punto P será

${\vec {v}}_{n1}^{\,P}=\sum _{i=1}^{n-1}{\vec {\omega }}_{(i+1)i}\times {\overrightarrow {O_{i}P}}$

Composiciones equivalentes

El resultado anterior indica que existen diferentes, infinitas de hecho, composiciones de movimientos que producen el mismo movimiento absoluto final. Desde el punto de vista cinemático, es lo mismo empujar una caja sobre el suelo, que montarla sobre rodillos para trasladarla.

Definimos entonces como equivalentes dos composiciones de N movimientos si producen el mismo movimiento absoluto. Es claro que esta relación es de equivalencia (verifica las propiedades reflexiva, simétrica y transitiva).

Matemáticamente, las condiciones para que dos composiciones de movimientos sean equivalentes son:

Misma velocidad angular neta

La velocidad angular neta, suma de las velocidades angulares relativas, debe ser la misma en las dos composiciones

${\vec {\omega }}=\sum _{i=1}^{n}{\vec {\omega }}_{i}=\sum _{i'=1}^{n'}{\vec {\omega }}_{i'}$

donde abreviamos la notación usando un solo subíndice para indicar la i-ésima velocidad angular. A la velocidad angular neta, que es un vector libre, como cada uno de los sumandos, se la denomina la resultante o vector rotación total del sistema.

Misma velocidad de un punto

Para un cierto punto O, la velocidad lineal resultante en ambas composiciones debe ser la misma

${\vec {v}}^{\,O}=\sum _{i=1}^{n}{\vec {v}}_{i}^{\,O}=\sum _{i'=1}^{n'}{\vec {v}}_{i'}^{\,O}$

Obsérvese que, si dos composiciones de movimientos conducen a una misma velocidad angular neta y a una misma velocidad en cierto punto O (igual reducción cinemática en O), esto implica que ambas composiciones conducen a idénticos campos de velocidades.

No es esta la única forma de establecer la equivalencia. Puesto que el campo de velocidades de un movimiento rígido se puede caracterizar de formas alternativas, cada una de ellas puede usarse para establecer la equivalencia. Así podemos requerir:

• Dos composiciones son equivalentes si producen la misma velocidad lineal en tres puntos dados (no alineados).

${\vec {v}}^{A}={\vec {v}}'^{A}$    ${\vec {v}}^{B}={\vec {v}}'^{B}$    ${\vec {v}}^{\,C}={\vec {v}}'^{\,C}$

El conjunto de todas las composiciones equivalentes forma una clase de equivalencia, que puede ser representada por uno cualquiera de sus elementos. Cuando este representante es un movimiento rígido elemental caracterizado por una velocidad angular y la velocidad lineal de un punto O se dice que hemos reducido la composición en el punto O.

En particular la reducción se dice canónica si el punto O pertenece al EIRMD.

De acuerdo con los posibles movimientos de un sólido obtenemos que los posibles resultados de las composiciones de N movimientos son:

${\vec {\omega }}=\sum _{i}{\vec {\omega }}_{i}$	${\vec {v}}^{\,O}=\sum _{i}{\vec {v}}_{i}^{\,O}$	Estado
$={\vec {0}}$	$={\vec {0}}$	Reposo
$={\vec {0}}$	$\neq {\vec {0}}$	Traslación
$\neq {\vec {0}}$	$={\vec {0}}$	Rotación
$\neq {\vec {0}}$	$\perp {\vec {\omega }}$	Rotación
$\neq {\vec {0}}$	$\not \perp {\vec {\omega }}$	Helicoidal

Casos particulares

Composición de dos o más traslaciones

La composición de cualquier número de traslaciones es otra traslación (incluyendo el reposo como caso particular)

${\vec {\omega }}=\sum _{i}\overbrace {{\vec {\omega }}_{i}} ^{={\vec {0}}}={\vec {0}}$

La velocidad de cualquiera de los puntos del sistema será la suma de las de las traslaciones individuales

${\vec {v}}^{P}=\sum _{i}{\vec {v}}_{i}^{P}=\sum _{i}{\vec {v}}_{i}^{\,O}={\vec {v}}^{\,O}$

En particular la composición de dos traslaciones iguales y opuestas es un estado de reposo.

La composición de N traslaciones es una traslación. Sin embargo, la composición de N rotaciones no es, en general, igual a una rotación. De hecho, como veremos, puede producir cualquier movimiento.

Par de rotaciones opuestas

Consideremos la composición de dos rotaciones puras cuyas velocidades angulares son iguales y opuestas

${\vec {\omega }}_{2}=-{\vec {\omega }}_{1}$

y cuyos ejes instantáneos de rotación, necesariamente paralelos, están separados una distancia $d$. La velocidad angular resultante de estas dos rotaciones es nula

${\vec {\omega }}={\vec {\omega }}_{1}+{\vec {\omega }}_{2}={\vec {\omega }}_{1}-{\vec {\omega }}_{1}={\vec {0}}$

Por tanto el movimiento resultante es uno de traslación o de reposo. Si $O_{1}$ y $O_{2}$ son sendos puntos en los respectivos ejes instantáneos de rotación, la velocidad de cualquier otro punto $P$ es

${\vec {v}}^{P}={\vec {v}}_{1}^{P}+{\vec {v}}_{2}^{P}={\vec {\omega }}_{1}\times {\overrightarrow {O_{1}P}}+{\vec {\omega }}_{2}\times {\overrightarrow {O_{2}P}}={\vec {\omega }}_{1}\times ({\overrightarrow {O_{1}P}}-{\overrightarrow {O_{2}P}})={\vec {\omega }}_{1}\times {\overrightarrow {O_{1}O_{2}}}$

Este resultado es independiente del punto P, pero no es nulo en general. Esto quiere decir que el resultado de dos rotaciones opuestas sobre ejes paralelos es una traslación con velocidad

${\vec {v}}^{P}={\vec {\omega }}_{1}\times {\overrightarrow {O_{1}O_{2}}}=\omega _{1}d{\vec {n}}$

con módulo

$\left|{\vec {v}}^{P}\right|=|{\vec {\omega }}_{1}\times {\overrightarrow {O_{1}O_{2}}}|=\omega _{1}|{\overrightarrow {O_{1}O_{2}}}|\,\mathrm {sen} \,\alpha =\omega _{1}d$

y dirección la normal al plano formado por los dos ejes instantáneos de rotación.

Ejemplos sencillos de esta composición lo tenemos en el caso de un vehículo que avanza sobre ruedas. Si el cuerpo del vehículo es el sólido 3, el suelo el sólido 1, y una rueda el sólido intermedio 2, ésta gira con la misma velocidad angular respecto al eje de la rueda que respecto a la línea de contacto con el suelo

${\vec {\omega }}_{23}={\vec {\omega }}_{21}$ ⇒ ${\vec {\omega }}_{32}=-{\vec {\omega }}_{21}$ ⇒ ${\vec {\omega }}_{31}={\vec {\omega }}_{32}+{\vec {\omega }}_{21}={\vec {0}}$

La celeridad de traslación del cuerpo del vehículo respecto al suelo será

$v^{P}=\omega _{21}R\,$

con $R$ el radio de la rueda, que es la distancia entre los dos ejes instantáneos de rotación.

El mismo principio se aplica a la traslación de las vagonetas de una noria, que mantienen su orientación a partir de la combinación de dos rotaciones opuestas.

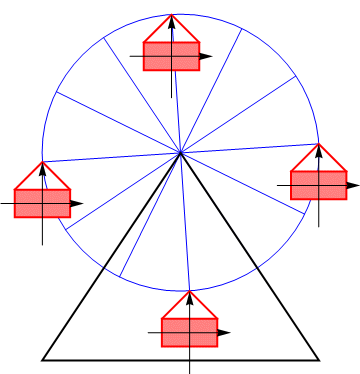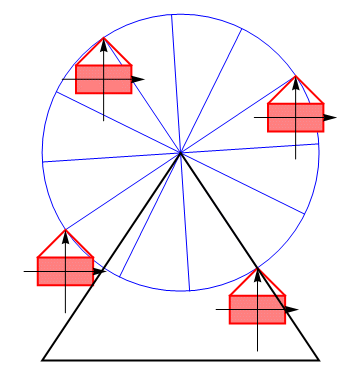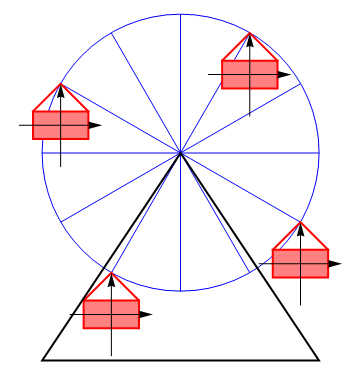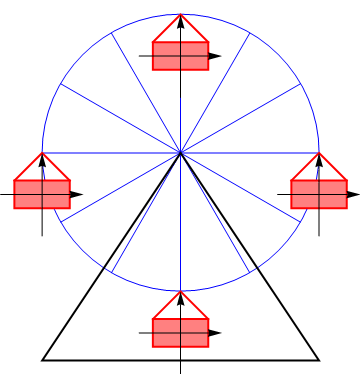
Jugando con los valores de ${\vec {\omega }}$ y de $d$ podemos obtener cualquier valor para la velocidad de traslación. Por tanto:

Toda traslación es equivalente a un par de rotaciones opuestas sobre ejes paralelos.

y, puesto que un movimiento rígido es siempre equivalente a una traslación más una rotación llegamos a que:

Todo movimiento rígido es equivalente a una composición de rotaciones puras.

Por tanto, el estudio de las composiciones de movimientos puede reducirse a considerar un conjunto de rotaciones alrededor de ciertos ejes instantáneos de rotación. De hecho, eligiendo adecuadamente los ejes, todo movimiento rígido puede escribirse como composición de solo dos rotaciones.

Caso de rotaciones concurrentes. Teorema de Varignon

Consideremos ahora el caso de N rotaciones puras cuyos ejes instantáneos de rotación pasan todos por el mismo punto O. El resultado de la composición tendrá una velocidad angular

${\vec {\omega }}=\sum _{i}{\vec {\omega }}_{i}$

mientras que la velocidad del punto O será nula

${\vec {v}}^{\,O}=\sum _{i}\overbrace {{\vec {v}}_{i}^{\,O}} ^{={\vec {0}}}={\vec {0}}$

Por tanto, la combinación de N rotaciones a través de ejes concurrentes (que pasan por un punto común), es otra rotación a través de un eje que pasa por el mismo punto y cuya velocidad angular es la suma de las velocidades angulares individuales. Este es el conocido como teorema de Varignon.

Un caso particular ilustrativo es el movimiento de una peonza, que puede verse como una composición de dos rotaciones: una alrededor de su eje (llamada movimiento de rotación), compuesta con una rotación de este eje alrededor de un eje vertical (llamada movimiento de precesión). Si además este eje se bambolea arriba y abajo (lo cual puede verse como una rotación alrededor de un eje horizontal), se dice que tiene además un movimiento de nutación.

Problemas

Problemas de movimiento relativo (G.I.T.I.)

Categoría Problemas de movimiento relativo (G.I.T.I.) no encontrada