Cinemática del sólido rígido (G.I.T.I.)

Concepto de sólido rígido

Compresibilidad nula

Una vez descrito el sistema más sencillo, formado por una sola partícula, podemos pasar a sistemas más complejos, considerándolos formados por un agregado de partículas interactuantes.

Existen toda una serie de leyes generales y teoremas de conservación para sistemas de partículas, pero aquí nos centraremos en un agregado muy concreto, que es el modelo denominado sólido rígido.

Los sistemas macroscópicos suelen clasificarse en diferentes estados de la materia: sólidos, líquidos, gases y plasmas. De estos, los tres últimos se agrupan conjuntamente en el concepto de fluidos, por oposición a los sólidos.

La diferencia entre un fluido y un sólido es que mientras el fluido se adapta a la forma del recipiente que lo contiene, el sólido no lo hace. También se distinguen en su comportamiento cuando se ejerce una fuerza tangente a su superficie (fuerza de cizalla). Un fluido adquiere una velocidad en la dirección de la fuerza (velocidad dependiente de la viscosidad del fluido), mientras que un sólido se deforma en dicha dirección.

Todos los sólidos son deformables cuando se aplica una fuerza sobre ellos, y el grado con que lo hacen se mide por su elasticidad. En el caso de un resorte, esta deformabilidad se mide con la constante de recuperación que aparece en la ley de Hooke.

Cuanto menor es la compresibilidad de un sólido (o mayor su constante de recuperación) más indeformable es, más fuerza es necesaria para conseguir una dilatación dada. Por ejemplo, de acuerdo con la ley de Hooke, la dilatación de un resorte viene dada por

$\Delta {\vec {r}}={\frac {\vec {F}}{k}}$

cuando $k\to \infty$ la deformación tiende a cero, sea cual sea la fuerza aplicada.

Un primer estudio de los sólidos consiste, por tanto, en hacer el modelo de sólido completamente indeformable, o sólido rígido.

Extensión indefinida

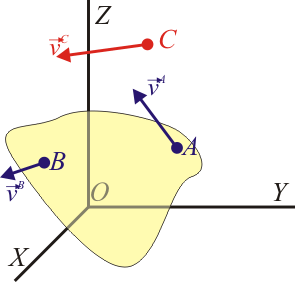
Todo sólido real está formado por un gran número de partículas materiales que ocupan una extensión finita en el espacio y poseen, en conjunto, una forma definida. Habrá puntos del espacio que estarán ocupados por alguna partícula material y habrá puntos en los que no habrá partícula alguna, bien porque se hallen en el exterior del sólido real, bien porque se encuentren en los intersticios entre las partículas materiales.

Sin embargo, desde el punto de vista del análisis de las velocidades y aceleraciones de un sólido, objeto de este tema, no necesitamos considerar este tamaño finito, ni la forma de los sólidos. Podemos suponer un sólido ideal extendido a todo el espacio, cuya distribución de velocidades es la correspondiente al sólido real que estemos estudiando. Al aplicar este sólido ideal a un caso concreto, basta tener en cuenta que para aquellos puntos exteriores (o interiores) al sólido en los que no hay partículas de este, no tiene sentido asignarles una velocidad.

Un sólido ideal queda entonces identificado por un cierto sistema de referencia, y cada punto del espacio, sean cuales sean sus coordenadas, puede tratarse como parte del sólido.

Condición de rigidez

Condición geométrica

Matemáticamente, un sólido rígido se caracteriza por ser un sistema de partículas tal que la distancia entre cada par de partículas que lo componen permanece constante en cada momento

$\left|{\vec {r}}_{i}-{\vec {r}}_{k}\right|=d_{ik}=\mathrm {cte}$

Esta es la condición geométrica de rigidez. Si empleamos letras para indicar las posiciones de cada partícula, esta condición se expresa

$\left|{\overrightarrow {AB}}\right|=d_{AB}=\mathrm {cte}$

Puesto que se aplica a cada par de partículas supone $N(N-1)/2$ vínculos geométricos (tantos como el número de pares de partículas), si bien muchos de ellos son redundantes en cuanto a que son consecuencia unos de otros.

Condición cinemática

Cada vínculo geométrico lleva asociado un vínculo cinemático, que establece una relación entre las velocidades posibles. Obtenemos estos vínculos derivando en la expresión de los vínculos geométricos.

Elevando al cuadrado

$\left({\vec {r}}_{i}-{\vec {r}}_{k}\right)\cdot \left({\vec {r}}_{i}-{\vec {r}}_{k}\right)=d_{ik}^{2}=\mathrm {cte}$

y derivando esta expresión respecto al tiempo obtenemos la condición sobre las velocidades.

$0=2\left({\frac {\mathrm {d} {\vec {r}}_{i}}{\mathrm {d} t}}-{\frac {\mathrm {d} {\vec {r}}_{k}}{\mathrm {d} t}}\right)\cdot \left({\vec {r}}_{i}-{\vec {r}}_{k}\right)=2\left({\vec {v}}_{i}-{\vec {v}}_{k}\right)\cdot \left({\vec {r}}_{i}-{\vec {r}}_{k}\right)$

Esta es la condición cinemática de rigidez, que podemos escribir

${\vec {v}}_{i}\cdot ({\vec {r}}_{i}-{\vec {r}}_{k})={\vec {v}}_{k}\cdot ({\vec {r}}_{i}-{\vec {r}}_{k})$

o, empleando letras, para cada par de puntos del sólido

${\vec {v}}^{A}\cdot {\overrightarrow {AB}}={\vec {v}}^{B}\cdot {\overrightarrow {AB}}$

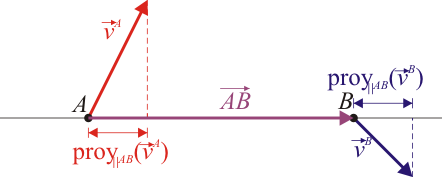
Dividiendo por la distancia entre las partículas A y B

${\vec {v}}^{A}\cdot {\frac {\overrightarrow {AB}}{|{\overrightarrow {AB}}|}}={\vec {v}}^{B}\cdot {\frac {\overrightarrow {AB}}{|{\overrightarrow {AB}}|}}$

siendo cada miembro la proyección de la velocidad en la dirección del vector ${\overrightarrow {AB}}$

$\mathrm {proy} _{\parallel {\overrightarrow {AB}}}({\vec {v}}^{A})=\mathrm {proy} _{\parallel {\overrightarrow {AB}}}({\vec {v}}^{B})$

La condición cinemática de rigidez implica que, dadas dos partículas, $A$ y $B$, la proyección de sus respectivas velocidades sobre la recta que las une es la misma. Por ello se dice que el campo de velocidades es equiproyectivo.

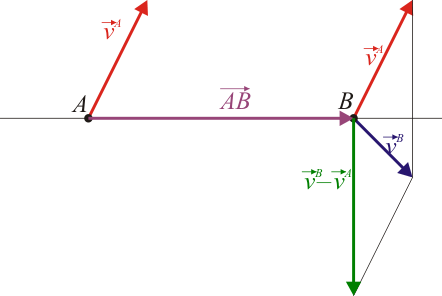
El que las dos proyecciones sean iguales quiere decir que la componente de las velocidades en esa dirección es la misma; las dos partículas avanzan o retroceden a lo largo de esa línea en igual medida, manteniendo su distancia relativa.

Otra forma de verlo es considerar que ${\vec {v}}^{B}-{\vec {v}}^{A}$ es la velocidad de la partícula $B$ respecto a la $A$

${\frac {\mathrm {d} \ }{\mathrm {d} t}}({\overrightarrow {AB}})={\frac {\mathrm {d} \ }{\mathrm {d} t}}({\overrightarrow {OB}})-{\frac {\mathrm {d} \ }{\mathrm {d} t}}({\overrightarrow {OA}})={\vec {v}}^{B}-{\vec {v}}^{A}$

y por tanto

$({\vec {v}}^{B}-{\vec {v}}^{A})\cdot {\overrightarrow {AB}}=0$

nos dice que la velocidad relativa de una partícula respecto a otra o es nula o es perpendicular a la recta que las une. Si nos montamos en una partícula del sólido y desde allí observamos a otra partícula cualquiera del mismo sólido, veremos que la otra partícula ni se acerca ni se aleja: o se mantiene en reposo o gira alrededor de nosotros moviéndose sobre una superficie esférica en cuyo centro nos hallamos.

Grados de libertad

El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ecuaciones de vínculos independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema.

¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos.

Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas.

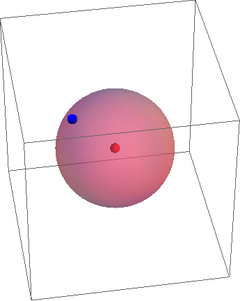
Situamos ahora una segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio $d_{12}$ alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables (latitud y longitud, por ejemplo).

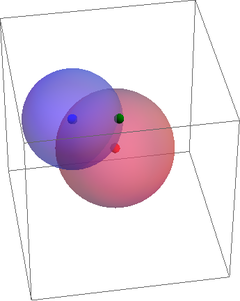
Una tercera partícula se encuentra a una distancia $d_{13}$ de la primera y a una distancia $d_{23}$ de la segunda. La posición de esta tercera partícula se encuentra por tanto sobre la circunferencia intersección de una esfera de radio $d_{13}$ alrededor de la primera y una esfera de radio $d_{23}$ alrededor de la segunda, y para localizar una posición concreta sobre una circunferencia solo necesitamos 1 variable.

Para una cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales.

Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición de un sólido rígido.

Una forma alternativa de comprobar que un sólido rígido tiene 6 grados de libertad consiste en pensar que la posición del sólido queda unívocamente determinada conocidas las posiciones de tres puntos no alineados del mismo. Tres puntos se describen mediante un total de 9 coordenadas (por ejemplo, 3 x 3 coordenadas cartesianas), pero esas 9 coordenadas no son independientes ya que deben satisfacer 3 ecuaciones de ligadura: las ecuaciones que establecen las distancias relativas constantes entre dichos puntos. Por tanto, el número de grados de libertad del sólido se reduce a 9 − 3 = 6.

Campo de velocidades

Cuando un sólido se mueve, cada uno de sus puntos lo hará, en principio, con una velocidad diferente. Tenemos entonces que la distribución de velocidades forma un campo vectorial

${\vec {v}}={\vec {v}}({\vec {r}})$

La velocidad de cada punto es un vector ligado a dicho punto y por tanto carece de sentido hablar de la “velocidad de un sólido”, como si fuera algo único. Podremos hablar de la velocidad de un punto del sólido, o, en su caso, de la velocidad de su centro de masas, pero no de la velocidad del sólido como un todo.

De acuerdo con el modelo de sólido ideal, podemos suponer esta distribución de velocidades como extendida a todo el espacio. En un sólido real, ${\vec {v}}({\vec {r}})$ solo tendrá significado en aquellos puntos en que haya partículas materiales.

La condición de rigidez impone limitaciones a las posibles distribuciones de velocidades. Solo aquellos movimientos que preservan las distancias entre los puntos son admisibles. Estos movimientos posibles se conocen como movimientos rígidos.

Puede demostrarse que la forma más general del campo de velocidades de un sólido (según el Teorema de Chasles) es

${\vec {v}}({\vec {r}})={\vec {v}}_{0}+{\vec {\omega }}\times {\vec {r}}$

siendo ${\vec {v}}_{0}$ y ${\vec {\omega }}$ dos vectores independientes de la posición (pero no del tiempo, no son constantes en general). Aquí ${\vec {r}}$ es la posición respecto a un cierto punto O que tomamos como origen de coordenadas.

Si etiquetamos la posición del origen por O y la de un punto cualquiera por P, la forma general del campo de velocidades puede escribirse como

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

• Al vector ${\vec {\omega }}$ se le conoce como velocidad angular (instantánea) o vector rotación del sólido. Más adelante se le da una interpretación geométrica.
• En principio ${\vec {v}}^{O}$ es una cantidad que resulta de la solución de las ecuaciones y que no tendría por qué tener un significado físico. No obstante, es evidente que coincide con la velocidad instantánea del punto O, lo que justifica su notación.
• Al punto O del cual se le da su velocidad se le denomina centro de reducción.
• Al conjunto $\{{\vec {v}}^{O},{\vec {\omega }}\}$ se denomina la reducción cinemática del campo de velocidades en el punto O.
• Si se cambia el centro de reducción a un punto diferente, A, se tendrá una reducción cinemática diferente $\{{\vec {v}}^{A},{\vec {\omega }}\}$. Más adelante veremos qué cambia y que no cambia al variar el centro de reducción.

Es inmediato comprobar que esta expresión del campo de velocidades satisface la condición cinemática de rigidez:

$\left\{{\begin{matrix}{\vec {v}}^{P}&=&{\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}\\{\vec {v}}^{Q}&=&{\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OQ}}\end{matrix}}\right.$ ⇒ ${\vec {v}}^{P}-{\vec {v}}^{Q}={\vec {\omega }}\times ({\overrightarrow {OP}}-{\overrightarrow {OQ}})={\vec {\omega }}\times {\overrightarrow {PQ}}$ ⇒  $({\vec {v}}^{P}-{\vec {v}}^{Q})\cdot {\overrightarrow {PQ}}=0$

La demostración en sentido inverso (que de la equiproyectividad se deduce la forma general del campo de velocidades) es bastante más elaborada. No obstante, puede justificarse la idea principal: la condición cinemática de rigidez implica la ortogonalidad entre la velocidad relativa y la posición relativa de P respecto a O

$({\vec {v}}^{P}-{\vec {v}}^{O})\cdot {\overrightarrow {OP}}=0$

y por tanto, la velocidad relativa puede expresarse como la posición relativa multiplicada vectorialmente por algo

${\vec {v}}^{P}-{\vec {v}}^{O}={\vec {\omega }}\times {\overrightarrow {OP}}$ ⇒ ${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

La complejidad de la demostración aparece al probar que ese vector ${\vec {\omega }}$ es el mismo para todos los pares de puntos.

El que el campo de velocidades quede descrito conociendo las tres componentes de ${\vec {v}}^{O}$ y las tres de ${\vec {\omega }}$ se corresponde con el que el movimiento de un sólido rígido tenga 6 = 3+3 grados de libertad.

No es esta la única forma de determinar la velocidad de cada punto. También podemos dar la velocidad de tres puntos no colineales del sólido (9 datos), sometidos a los 3 vínculos de que las distancias entre ellos permanecen constantes.

Un aspecto hay que remarcar no una, sino cada vez que se emplea la fórmula anterior: está expresión sólo nos da la distribución de velocidades en un instante dado. Nos da una instantánea del movimiento. Pero, dado que ${\vec {v}}^{O}$ y ${\vec {\omega }}$ son funciones del tiempo, la fórmula no nos dice dónde van a estar las partículas un intervalo de tiempo después. El movimiento de un sólido puede ser extremadamente complicado.

Estado de reposo

El caso más simple de estado de movimiento es el que tiene

${\vec {v}}^{O}={\vec {0}}$    ${\vec {\omega }}={\vec {0}}$

En este caso todos los puntos del sólido se encuentran en reposo:

${\vec {v}}^{P}={\vec {0}}$

Equivalentemente, este estado se puede enunciar diciendo que si tres puntos no colineales de un sólido se encuentran en reposo, entonces todos los demás también están en reposo.

El estado de reposo puede ser

Instantáneo

Si la velocidad de todos los puntos se anula en un momento dado, para al instante siguiente dejar de ser nula.

Permanente

Si este estado se mantiene durante un cierto intervalo de tiempo.

Movimiento de traslación

Un movimiento de traslación se caracteriza porque (siendo ${\vec {v}}^{O}\neq {\vec {0}}$) la velocidad angular es nula:

${\vec {\omega }}={\vec {0}}$

En este caso, el campo de velocidades se reduce a

${\vec {v}}^{P}={\vec {v}}^{O}$

esto es, todos los puntos del sólido se mueven con la misma velocidad instantánea. Cuando esto ocurre se dice que el sólido experimenta un movimiento de traslación.

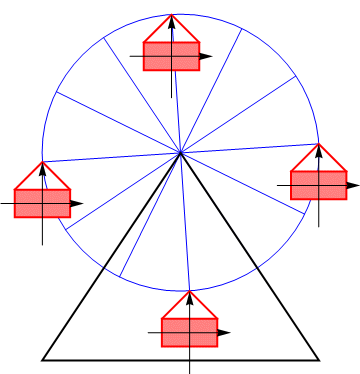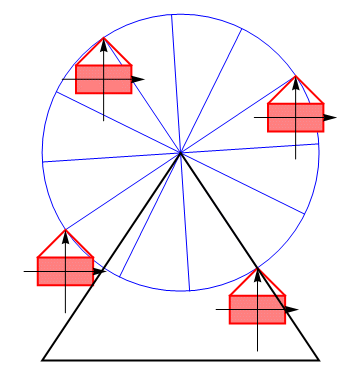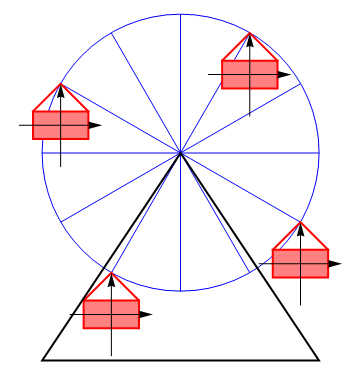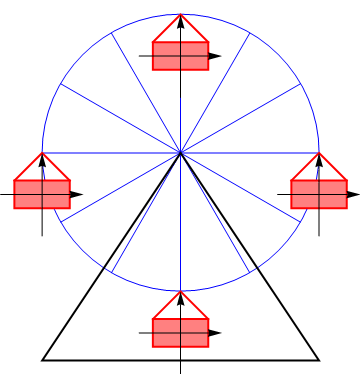
Si fijamos un sistema de ejes al sólido, estos mantienen su orientación en un movimiento de traslación.

Equivalentemente, el movimiento de traslación se puede enunciar afirmando que si tres puntos no colineales del sólido tienen la misma velocidad, todos los demás también tienen la misma.

Hay que insistir en que hablamos de velocidades instantáneas y del movimiento relativo de los diferentes puntos del sólido. Un movimiento de traslación NO significa que el sólido se mueve en línea recta, o a velocidad constante.

Por ejemplo, consideremos el movimiento de un vagón de una noria. Puesto que éste no se da la vuelta, sino que conserva en todo momento su orientación vertical, llegamos a la conclusión de que el sólido experimenta un movimiento de traslación. Cada uno de sus puntos se mueve en cada instante con la misma velocidad que el resto de los puntos, aunque esta velocidad sea cambiante.

Traslación permanente

En el caso más restrictivo

${\vec {\omega }}={\vec {0}}\quad \forall t$

implica un movimiento de traslación permanente: los ejes ligados al sólido conservan su orientación en cada instante y el movimiento de cada uno de los puntos del sólido reproduce exactamente el de cualquier otro de ellos.

En una traslación permanente, la posición relativa de un punto cualquiera Q respecto a otro punto arbitrario P se mantiene constante en módulo, dirección y sentido.

${\frac {\mathrm {d} \ }{\mathrm {d} t}}({\overrightarrow {PQ}})={\frac {\mathrm {d} \ }{\mathrm {d} t}}({\overrightarrow {OQ}})-{\frac {\mathrm {d} \ }{\mathrm {d} t}}({\overrightarrow {OP}})={\vec {v}}^{Q}-{\vec {v}}^{P}={\vec {0}}$

Un movimiento de traslación permanente no tiene por qué ser ni rectilíneo ni uniforme. Como en el caso de la noria, es posible que cada uno de los puntos describa una circunferencia en torno a un centro (siendo este centro diferente para cada punto del sólido).

Movimiento de rotación

Artículo completo: Rotación instantánea de un sólido rígido

Propiedades generales

Supongamos ahora que

${\vec {v}}^{O}={\vec {0}}$

de forma que la velocidad instantánea de cada punto se reduce a

${\vec {v}}^{P}={\vec {\omega }}\times {\overrightarrow {OP}}$

Esta forma del campo de velocidades posee una serie de propiedades que lo identifican como movimiento de rotación:

• La velocidad del punto O es nula

${\vec {v}}^{O}={\vec {0}}$

• Todos los puntos situados en la recta que pasa por O y tiene la dirección de ${\vec {\omega }}$ poseen velocidad nula:

${\overrightarrow {OP}}\parallel {\vec {\omega }}\qquad \Rightarrow \qquad {\vec {v}}^{P}={\vec {\omega }}\times {\overrightarrow {OP}}={\vec {0}}$

Esta línea se conoce como eje instantáneo de rotación (EIR).

• Dos puntos situados sobre una recta paralela al eje de rotación poseen la misma velocidad

${\overrightarrow {PQ}}\parallel {\vec {\omega }}$ ⇒ ${\vec {v}}^{Q}={\vec {\omega }}\times {\overrightarrow {OQ}}={\vec {\omega }}\times ({\overrightarrow {OP}}+{\overrightarrow {PQ}})={\vec {\omega }}\times {\overrightarrow {OP}}={\vec {v}}^{P}$

Esto quiere decir que la estructura del campo de velocidades es la misma si consideremos planos paralelos entre sí y perpendiculares al EIR.

• Inversamente, si dos puntos poseen la misma velocidad instantánea, el EIR es paralelo a la recta que pasa por estos dos puntos

${\vec {v}}^{P}={\vec {v}}^{Q}\qquad \Rightarrow \qquad {\vec {\omega }}\parallel {\overrightarrow {PQ}}$

• La velocidad de que cualquier otro punto es perpendicular al eje de rotación.

${\vec {v}}^{P}={\vec {\omega }}\times {\overrightarrow {OP}}\perp {\vec {\omega }}$

Por tanto, si consideramos un plano perpendicular al eje instantáneo de rotación por un punto $I$ de este mismo eje, todos los puntos de este plano poseen una velocidad contenida en dicho plano.

El que las velocidades de todos los puntos estén contenidas en planos paralelos implica que para cualesquiera tres puntos del sólido debe anularse el producto mixto

${\vec {v}}^{A}\cdot ({\vec {v}}^{B}\times {\vec {v}}^{C})=0$

• Todos los puntos a la misma distancia del eje poseen la misma celeridad. Si consideramos un plano perpendicular al eje instantáneo de rotación, e I es la intersección del eje y el plano, entonces

$|{\vec {v}}^{P}|=|{\vec {\omega }}\times {\overrightarrow {OP}}|=|{\vec {\omega }}\times \overbrace {\overrightarrow {IP}} ^{\perp {\vec {\omega }}}|=|{\vec {\omega }}||{\overrightarrow {IP}}|$

Para todos los puntos situados a la misma distancia del eje $d=|{\overrightarrow {IP}}|$, la rapidez vale $v^{P}=\omega d$.

• La celeridad de cada punto es proporcional a su distancia al eje. Justo en el eje la rapidez es nula, aumentando linealmente con $d$, la distancia al eje.
• El sentido de las velocidades cumple la regla de la mano derecha respecto al vector ${\vec {\omega }}$.

Alternativamente, el movimiento de rotación se puede caracterizar a partir del estado de dos puntos cuya velocidad es nula y un tercero, P, no colineal con ellos, con velocidad no nula, ${\vec {v}}^{P}$. En ese caso el resto del campo de velocidades es el de una rotación pura con eje el que pasa por los dos primeros puntos y con velocidad angular de módulo $v^{P}/d$ siendo $d$ la distancia de P a la recta que pasa por los otros dos.

Al estudiar el movimiento de rotación y describir las velocidades según la ley se puede adquirir la idea errónea de que las partículas del sólido describe un movimiento circular. Eso NO es correcto. Lo que hemos hecho es describir la distribución instantánea de velocidades, esto es, qué velocidad tiene cada punto del sólido en un instante dado, pero no hemos analizado cómo se mueve cada punto a lo largo del tiempo (en términos llanos, hemos tomado una fotografía, no una película de vídeo).

Consideremos el caso de un cilindro que rueda sobre el suelo. La línea de contacto esta formada por puntos con velocidad nula y por tanto se trata de un eje instantáneo de rotación. El cilindro está efectuando una rotación pura instantánea en torno a esta línea de contacto (y no respecto al eje del cilindro, como podría pensarse), pero la trayectoria de cada punto del cilindro no es una circunferencia, sino una cicloide (técnicamente, para los puntos que no son de la superficie exterior es una cicloide acortada).

La razón es que aunque instantáneamente esté rotando en torno a esta línea, el eje de rotación va cambiando en el tiempo.

Movimiento con un punto fijo

Supongamos el caso particular

${\vec {v}}^{O}={\vec {0}}\qquad \forall t$

En este caso tenemos un punto O para el cual la velocidad es siempre nula y, por tanto, se encuentra permanentemente en reposo.

El movimiento del sólido es, en cada instante una rotación en torno a un eje que pasa por este punto.

No podemos asegurar que haya más puntos permanentemente en reposo, ya que la orientación del eje de giro puede cambiar con el tiempo haciendo que los puntos instantáneamente en reposo sean diferentes en cada momento. La trayectoria de cada punto individual puede ser extremadamente complicada. NO describen una circunferencia.

El ejemplo típico de movimiento de un sólido con un punto fijo es el balanceo de una peonza o de un giróscopo.

Movimiento con un eje fijo

Supongamos el caso aun más restrictivo

${\vec {v}}^{O}={\vec {0}}\qquad \qquad {\vec {\omega }}=\omega (t){\vec {k}}\qquad \forall t$

esto es, la velocidad angular, aunque variable en módulo, posee siempre la misma dirección.

En este caso, el eje de rotación es siempre el mismo y todos sus puntos están permanentemente en reposo. Se dice entonces que tenemos un movimiento con un eje fijo (eje permanente de rotación), y que el sólido es un rotor.

Este es el típico movimiento de un sólido ensartado a un eje permanente. Para este caso, sí es cierto que la trayectoria de los diferentes puntos es una circunferencia (o un arco de circunferencia).

Un ejemplo es el de un péndulo cuya barra es rígida y por tanto de longitud constante. La lenteja del péndulo efectúa un movimiento que, aunque oscilante, es de rotación en torno a un eje fijo.

Movimiento helicoidal

Artículo completo: Movimiento helicoidal de un sólido rígido

Consideremos ahora el caso más general en que ni ${\vec {v}}^{O}$ ni ${\vec {\omega }}$ son nulos, pero sí paralelos:

${\vec {v}}^{O}=v_{d}{\frac {\vec {\omega }}{\omega }}$

En la expresión anterior ${\vec {\omega }}/\omega$ representa el unitario en la dirección de la velocidad angular. $v_{d}$ es la componente de la velocidad del punto O en la dirección de este unitario. A esta cantidad se la conoce como velocidad de deslizamiento. Puede ser tanto negativa como positiva, dependiendo de si el avance es el sentido de la velocidad angular u opuesto a él.

Este campo de velocidades posee una serie de propiedades:

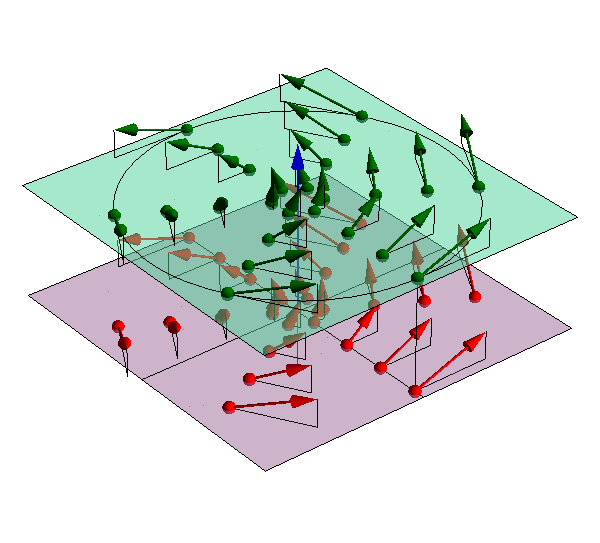
• La velocidad del punto O es paralela a la velocidad angular.
• Los puntos de la recta que pasa por O y tiene la dirección de la velocidad angular poseen la misma velocidad, paralela a esta dirección.

${\overrightarrow {OI}}\parallel {\vec {\omega }}\qquad \Rightarrow \qquad {\vec {v}}^{I}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OI}}={\vec {v}}^{O}=v_{d}{\frac {\vec {\omega }}{\omega }}$

Estos puntos forman el eje instantáneo de rotación y mínimo deslizamiento (EIRMD).

• Dos puntos situados sobre una recta paralela al eje de rotación poseen la misma velocidad

${\overrightarrow {PQ}}\parallel {\vec {\omega }}$ ⇒ ${\vec {v}}^{Q}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OQ}}=$${\vec {v}}^{O}+{\vec {\omega }}\times ({\overrightarrow {OP}}+{\overrightarrow {PQ}})={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}={\vec {v}}^{P}$

Esto quiere decir, de nuevo que la estructura del campo de velocidades es la misma si consideremos planos paralelos entre sí y perpendiculares al EIRMD. Nos basta con estudiar lo que ocurre en uno de estos planos.

• Inversamente, si dos puntos poseen la misma velocidad instantánea, el EIRMD es paralelo a la recta que pasa por estos dos puntos

${\vec {v}}^{P}={\vec {v}}^{Q}\qquad \Rightarrow \qquad {\vec {\omega }}\parallel {\overrightarrow {PQ}}$

• Para cada punto, la proyección de la velocidad paralela a la velocidad angular tiene el mismo valor. Para cualquier punto tenemos

${\vec {v}}^{P}=\overbrace {{\vec {v}}^{O}} ^{\parallel {\vec {\omega }}}+\overbrace {{\vec {\omega }}\times {\overrightarrow {OP}}} ^{\perp {\vec {\omega }}}$ ⇒ ${\begin{cases}{\vec {v}}_{\parallel }^{P}={\vec {v}}^{O}&(\parallel {\vec {\omega }})\\{\vec {v}}_{\perp }^{P}={\vec {\omega }}\times {\overrightarrow {OP}}&(\perp {\vec {\omega }})\end{cases}}$

con lo que la proyección paralela para cada punto es

$\mathrm {proy} _{\parallel {\vec {\omega }}}({\vec {v}}^{P})={\vec {v}}^{P}\cdot {\frac {\vec {\omega }}{\omega }}={\vec {v}}^{O}\cdot {\frac {\vec {\omega }}{\omega }}=\mathrm {proy} _{\parallel {\vec {\omega }}}({\vec {v}}^{O})=v_{d}$

esto es, además de moverse lateralmente alrededor del eje, todos los puntos avanzan en la dirección del eje con la misma velocidad.

• Para todos los puntos situados a la misma distancia $d$ del EIRMD, la proyección de la velocidad ortogonal a la velocidad angular tiene el mismo valor. Considerando el plano que pasa por O y es ortogonal al EIRMD tenemos que

$\mathrm {proy} _{\perp {\vec {\omega }}}({\vec {v}}^{P})=|{\vec {\omega }}\times {\overrightarrow {OP}}|=\omega d$

Esta componente aumenta linealmente con la distancia al EIRMD.

• Como consecuencia de lo anterior, la rapidez de todos los puntos situados a la misma distancia del eje es la misma, y su velocidad forma el mismo ángulo con la velocidad angular.

$v^{P}={\sqrt {(v^{O})^{2}+\omega ^{2}d^{2}}}$    $\mathrm {tg} \beta ={\frac {\omega d}{v^{O}}}$

• El sentido de la velocidad cumple la regla de la mano derecha respecto a la velocidad angular.

Caso general

Supongamos ahora el caso general, con ${\vec {v}}^{O}$ y ${\vec {\omega }}$ arbitrarios, nulos o no y paralelos o no, de forma que la velocidad de un punto P tiene la forma

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

Nos preguntamos entonces cómo es este movimiento general; si será equivalente a alguno de los casos anteriores o si pertenecerá a algún tipo aun no descrito.

La forma más sencilla de caracterizarlo consiste en determinar en primer lugar los llamados invariantes del movimiento.

Invariantes

En la expresión general del campo de velocidades de un sólido

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

destaca un punto O, respecto al que se miden los vectores de posición. Este punto se denomina centro de reducción y al par $\{{\vec {v}}^{O},{\vec {\omega }}\}$ se lo denomina reducción del campo de velocidades en el punto O. ¿Cómo cambia la expresión del campo de velocidades si elegimos un punto diferente, A, como centro de reducción? Si

${\overrightarrow {OP}}={\overrightarrow {OA}}+{\overrightarrow {AP}}$

resulta, sustituyendo

${\vec {v}}^{P}=({\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OA}})+{\vec {\omega }}\times {\overrightarrow {AP}}={\vec {v}}^{A}+{\vec {\omega }}\times {\overrightarrow {AP}}$

esto es, que la expresión resultante es análoga a la original, sin más que sustituir ${\vec {v}}^{O}$ por la velocidad del nuevo centro de reducción. Así obtenemos la reducción $\{{\vec {v}}^{A},{\vec {\omega }}\}$.

Comparando las reducciones correspondientes a diferentes centros de reducción, observamos que hay ciertas cantidades que tienen el mismo valor para todos ellos. Estas cantidades se denominan invariantes:

Primer invariante (velocidad angular)

El vector ${\vec {\omega }}$ que aparece en la expresión general del campo de velocidades es la misma para todos los centros de reducción, por ello no lleva ningún tipo de superíndice. Este vector es equivalente a un vector libre.

Segundo invariante (velocidad de deslizamiento)

Para todos los centros de reducción, la componente de la velocidad en la dirección de la velocidad angular es la misma para todos ellos:

$\mathrm {proy} _{\parallel {\vec {\omega }}}({\vec {v}}^{A})={\frac {{\vec {v}}^{A}\cdot {\vec {\omega }}}{\omega }}={\frac {{\vec {v}}^{O}\cdot {\vec {\omega }}}{\omega }}=\mathrm {proy} _{\parallel {\vec {\omega }}}({\vec {v}}^{O})=v_{d}$

Análisis del caso general

Nos planteamos entonces como caracterizar un movimiento del que conocemos la reducción en un punto concreto $\{{\vec {v}}^{O},{\vec {\omega }}\}$, con ${\vec {v}}^{O}$ y ${\vec {\omega }}$ arbitrarios, nulos o no y paralelos o no, de forma que la velocidad de un punto P tiene la forma

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}$

Deseamos saber si este movimiento general se reduce a alguno de los que ya conocemos, o es uno diferente. Resolveremos esta cuestión con ayuda de los invariantes del movimiento.

En primer lugar, si ${\vec {\omega }}={\vec {0}}$ la solución ya la conocemos. El movimiento es una traslación (que incluye el reposo como caso particular).

Supongamos que ${\vec {\omega }}\neq {\vec {0}}$. Veremos que este movimiento general se reduce a un movimiento helicoidal, que contiene como caso particular a la rotación pura, si $v_{d}=0$.

Para ello, en lugar de analizar el movimiento alrededor de O, lo que haremos es buscar un nuevo centro de reducción I, tal que en él la reducción del movimiento $\{{\vec {v}}^{I},{\vec {\omega }}\}$ sea la más sencilla posible. Esta reducción mínima se denomina la reducción canónica.

Para este punto I, como para cualquier otro del sólido, su velocidad se podrá descomponer en una parte paralela a la velocidad angular y una parte perpendicular a ella, en la forma

${\vec {v}}^{I}={\vec {v}}^{O}+\overbrace {{\vec {\omega }}\times {\overrightarrow {OI}}} ^{\perp {\vec {\omega }}}\qquad \Rightarrow \qquad {\begin{cases}{\vec {v}}_{\parallel }^{I}={\vec {v}}_{\parallel }^{O}&(\parallel {\vec {\omega }})\\{\vec {v}}_{\perp }^{I}={\vec {v}}_{\perp }^{O}+{\vec {\omega }}\times {\overrightarrow {OI}}&(\perp {\vec {\omega }})\end{cases}}$

La parte paralela es la misma para todos los posibles centros de reducción y tiene por componente el segundo invariante la velocidad de deslizamiento

${\vec {v}}_{\parallel }^{I}={\vec {v}}_{\parallel }^{O}=v_{d}{\vec {u}}\qquad \qquad v_{d}={\frac {{\vec {v}}^{O}\cdot {\vec {\omega }}}{\omega }}\qquad \qquad {\vec {u}}={\frac {\vec {\omega }}{\omega }}$

Para la parte perpendicular, observamos que la correspondiente al vector O puede hallarse mediante la fórmula general

${\vec {v}}_{\perp }^{O}=-{\frac {{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {v}}^{O})}{\omega ^{2}}}$

de forma que la parte perpendicular de la velocidad del punto I puede escribirse como

${\vec {v}}_{\perp }^{I}={\vec {v}}_{\perp }^{O}+{\vec {\omega }}\times {\overrightarrow {OI}}={\vec {\omega }}\times \left(-{\frac {{\vec {\omega }}\times {\vec {v}}^{O}}{\omega ^{2}}}+{\overrightarrow {OI}}\right)$

La reducción canónica, esto es, la más sencilla, se consigue cuando conseguimos anular esta componente (ya que la paralela es invariante y por tanto intocable). Esta cantidad se anula en los puntos

${\overrightarrow {OI}}={\frac {{\vec {\omega }}\times {\vec {v}}^{O}}{\omega ^{2}}}+\lambda {\vec {\omega }}$

Esta es la ecuación de una recta que pasa por el punto dado por la primera fracción y con dirección la de la velocidad angular. Para los puntos situados sobre esta recta la velocidad tiene solo componente paralela a la velocidad angular, siendo esta componente igual a la velocidad de deslizamiento

${\vec {v}}^{I}={\vec {v}}_{\parallel }^{I}=v_{d}{\vec {u}}={\frac {({\vec {v}}^{O}\cdot {\vec {\omega }}){\vec {\omega }}}{\omega ^{2}}}$

Esta recta es el eje instantáneo de rotación y mínimo deslizamiento (EIRMD) de este movimiento. Si tomamos como centro de reducción un punto de este eje, el campo de velocidades se reduce a

${\vec {v}}^{P}={\vec {v}}^{I}+{\vec {\omega }}\times {\overrightarrow {IP}}$    $({\vec {v}}^{I}=v_{d}{\vec {u}},\ {\vec {\omega }}=\omega {\vec {u}})$

que, dependiendo del valor del segundo invariante, corresponde a:

Rotación pura

Si ${\vec {v}}^{O}\cdot {\vec {\omega }}=0$ la velocidad de deslizamiento es nula, y la única componente de la velocidad es la de rotación en torno al eje que pasa por I y lleva la dirección de ${\vec {\omega }}$ (eje instantáneo de rotación, EIR).

Movimiento helicoidal

Si ${\vec {v}}^{O}\cdot {\vec {\omega }}\neq 0$ el campo de velocidades se compone de una componente de avance en la dirección de ${\vec {\omega }}$ y una de rotación en torno al eje que pasa por I y lleva la dirección de ${\vec {\omega }}$ (eje instantáneo de rotación y mínimo deslizamiento, EIRMD).

Cuando reducimos el movimiento en un punto del EIRMD obtenemos el par $\{{\vec {v}}^{I},{\vec {\omega }}\}$ donde siempre se cumplirá ${\vec {v}}^{I}\times {\vec {\omega }}={\vec {0}}$. A esta reducción se la denomina reducción canónica del movimiento.

Considerando todos los casos conjuntamente, podemos hacer el siguiente esquema:

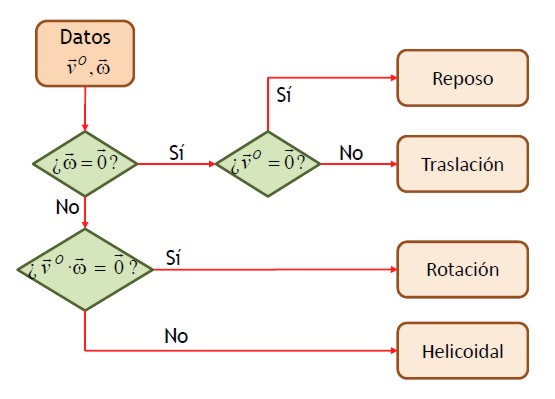
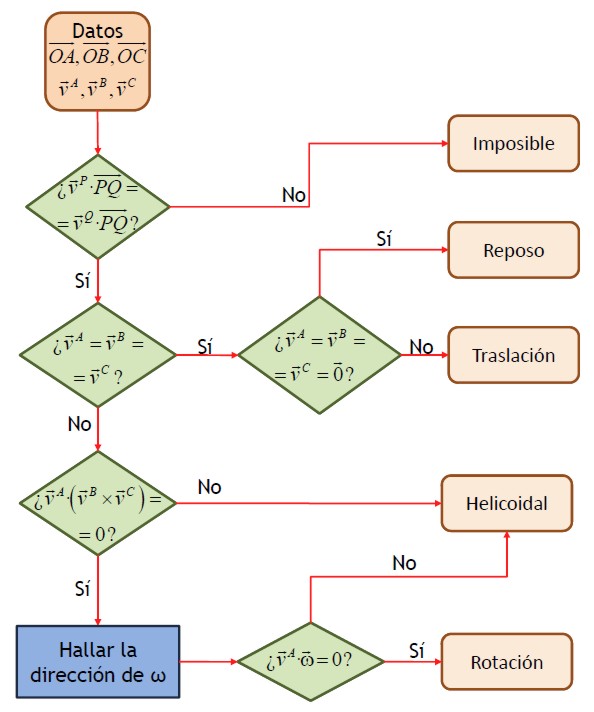
Si lo que conocemos es la velocidad de tres puntos no alineados, A, B y C, podemos clasificar el movimiento comprobando, en primer lugar, si se verifica la condición de equiproyectividad; en segundo lugar, si las tres velocidades son iguales; por último, verificamos si las tres velocidades son no coplanarias (en cuyo caso se trata de un movimiento helicoidal):

Campo de aceleraciones

Derivando respecto al tiempo en la expresión del campo de velocidades obtenemos la aceleración de punto P

${\vec {a}}^{P}={\frac {\mathrm {d} {\vec {v}}^{P}}{\mathrm {d} t}}={\frac {\mathrm {d} {\vec {v}}^{O}}{\mathrm {d} t}}+{\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}\times {\overrightarrow {OP}}+{\vec {\omega }}\times {\frac {\mathrm {d} ({\overrightarrow {OP}})}{\mathrm {d} t}}$

Siendo

${\frac {\mathrm {d} {\vec {v}}^{O}}{\mathrm {d} t}}={\vec {a}}^{O}$    ${\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}={\vec {\alpha }}$    ${\frac {\mathrm {d} ({\overrightarrow {OP}})}{\mathrm {d} t}}={\vec {v}}^{P}-{\vec {v}}^{O}={\vec {\omega }}\times {\overrightarrow {OP}}$

llegamos a la expresión del campo de aceleraciones

${\vec {a}}^{P}={\vec {a}}^{O}+{\vec {\alpha }}\times {\overrightarrow {OP}}+{\vec {\omega }}\times ({\vec {\omega }}\times {\overrightarrow {OP}})$

A diferencia del campo de velocidades, el campo de aceleraciones no es equiproyectivo:

$({\vec {a}}^{P}-{\vec {a}}^{O})\cdot {\overrightarrow {OP}}={\overrightarrow {OP}}\cdot ({\vec {\omega }}\times ({\vec {\omega }}\times {\overrightarrow {OP}}))=-\left|{\vec {\omega }}\times {\overrightarrow {OP}}\right|^{2}$

Solo en el caso de traslación o reposo instantáneos se cumplirá la equiproyectividad.

Dos consideraciones prácticas.

• El campo de aceleraciones requiere conocer tres vectores (esto es, 9 datos, frente a los 6 del campo de velocidades):
  • La aceleración de un punto O, ${\vec {a}}^{O}$.
  • La velocidad angular instantánea, ${\vec {\omega }}$.
  • La aceleración angular, ${\vec {\alpha }}$, derivada temporal de la velocidad angular.
• La aceleración de un punto P se puede calcular derivando la velocidad sólo si se conoce ésta como función del tiempo ${\vec {v}}^{P}(t)$. Conocerla en un instante no es suficiente.

Problemas

Problemas de cinemática del sólido rígido (G.I.T.I.)

Categoría Problemas de cinemática del sólido rígido (G.I.T.I.) no encontrada