Diferencia entre las páginas «Segunda Convocatoria Ordinaria 2014/15 (G.I.C.)» y «Partícula deslizando sobre disco con muelle (Ene. 2021 G.I.C.)»
(Página creada con «= Partícula sobre rampa con muelle, tirada por un cable = right Una partícula de masa <math>m</math> sube deslizándose por un plano inclinado bajo la acción de un cable que tire de ella. El contacto con el plano es rugoso y está caracterizado por un coeficiente de rozamiento dinámico <math>\mu</math>. El plano inclinado forma…») |
(Página creada con «= Enunciado = right Una partícula de masa <math>10m_0</math> desliza sin rozamiento sobre un semidisco de radio <math>R</math>. En el instante inicial la partícula se encuentra en el punto <math>A</math> y se le imparte una velocidad horizontal de rapidez <math>v_0=\lambda\sqrt{gR}</math>, siendo <math>\lambda</math> un número real positivo. La masa está conectada a un muelle de constante elástica <math>k=25m_0g/…») |
||
| Línea 1: | Línea 1: | ||
= | = Enunciado = | ||
[[ | [[File:F1GIC-particulaDiscoMuelle-enunciado.png|right]] | ||
Una partícula de masa <math> | Una partícula de masa <math>10m_0</math> desliza sin rozamiento sobre un semidisco de radio <math>R</math>. En el instante inicial la partícula se encuentra en el punto <math>A</math> y se le imparte una velocidad horizontal de rapidez <math>v_0=\lambda\sqrt{gR}</math>, siendo <math>\lambda</math> un número real positivo. La masa está conectada a un muelle de constante elástica <math>k=25m_0g/R</math> y longitud natural nula. El otro extremo del muelle está conectado al punto <math>B</math> que se mueve de modo que el muelle permanece siempre horizontal. | ||
#Escribe los vectores de la base cartesiana en la base polar. | |||
#Escribe la expresión de la fuerza ejercida por el muelle sobre la masa en la base polara. | |||
#Escribe la expersión que da la velocidad de la partícula para el ángulo <math>\theta=\beta</math>, con <math>\mathrm{sen}\,\beta=3/5</math> y <math>\cos\beta=4/5</math>. | |||
#¿Que condición debe cumplir <math>\lambda</math> para que la partícula se separe del disco en ese ángulo <math>\beta</math>? | |||
y | |||
= Solución = | |||
'''Vectores cartesianos en la base polar ''' | |||
Observando los vectores de la base indicados en la figura del enunciado tenemos | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{\imath} = \cos\theta\,\vec{u}_r - \mathrm{sen}\,\theta\,\vec{u}_{\theta},\\ | |||
\vec{\jmath} = \mathrm{sen}\,\theta\,\vec{u}_r + \cos\theta\,\vec{u}_{\theta}. | |||
\end{array} | |||
</math> | |||
</center> | |||
''' Fuerza ejercida por el muelle ''' | |||
Dado que tiene longitud natural nula la fuerza ejercida por el muelle puede escribirse | |||
<center> | |||
<math> | |||
\vec{F}_k = -k\,\overrightarrow{BC}. | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | |||
<math> | |||
\overrightarrow{BC} = \overline{BC}\,\vec{\imath} = R\cos\theta\,\vec{\imath}. | |||
</math> | |||
</center> | |||
Utilizando la expresión de <math>\vec{\imath}</math> del apartado anterior tenemos | |||
<center> | |||
<math> | |||
\vec{F}_k = -kR\cos^2\theta\,\vec{u}_r + kR\,\mathrm{sen}\,\theta\cos\theta\,\vec{u}_{\theta} | |||
= -25m_0g\cos^2\theta\,\vec{u}_r + 25m_0g\,\mathrm{sen}\,\theta\cos\theta\,\vec{u}_{\theta}. | |||
</math> | |||
</center> | |||
''' Expresión de la velocidad de la partícula ''' | |||
Como el vínculo es liso, las únicas fuerzas que hacen trabajo son las debidas a la gravedad y al muelle, que son conservativas. Por tanto la energía mecánica se conserva. En el punto <math>A</math> vale | |||
<center> | |||
<math> | |||
E_A = \dfrac{1}{2}mv_A^2 + mgR = 5m_0gR\lambda^2 + 10m_0gR. | |||
</math> | |||
</center> | |||
Hemos escogido como altura de referencia para la energía potencial la de la base del semidisco. Para el ángulo <math>\beta</math> tenemos | |||
<center> | |||
<math> | |||
E = \dfrac{1}{2}mv^2 + mgR\mathrm{sen}\,\beta + \dfrac{1}{2}k(R\cos\beta)^2 = | |||
5m_0v_{\beta}^2 + 14m_0gR. | |||
= | |||
</math> | |||
</center> | |||
Evaluando para <math>\theta=\beta</math> e igualando las dos expresiones obtenemos | |||
<center> | |||
<math> | |||
v_{\beta} = \sqrt{\dfrac{gR}{5}}\,\sqrt{5\lambda^2-4} | |||
</math> | |||
</center> | |||
''' Condición para que la partícula se separe de la superficie ''' | |||
Cuando la partícula se separa la normal que ejerce la superficie sobre ella se anula, pues ya no es necesaria para que la partícula no penetre en el disco. Las fuerzas que actúan sobre la partícula son, en la base polar | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{P} = -mg\,\vec{\jmath} = -10m_0g\,\mathrm{sen}\,\theta\,\vec{u}_r - 10m_0g\cos\theta\,\vec{u}_{\theta},\\ | |||
\vec{N} = N\,\vec{u}_r,\\ | |||
\vec{F}_k = -25m_0g\cos^2\theta\,\vec{u}_r + 25m_0g\,\mathrm{sen}\,\theta\cos\theta\,\vec{u}_{\theta}. | |||
\end{array} | |||
</math> | |||
</center> | |||
La aceleración de la partícula es | |||
<center> | |||
<math> | |||
\vec{a} = -R\dot{\theta}^2\,\vec{u}_r + R\ddot{\theta}\,\vec{u}_{\theta}. | |||
</math> | |||
</center> | |||
A partir de la Segunda Ley de Newton obtenemos | |||
<center> | |||
<math> | |||
m\vec{a} = \vec{P} + \vec{N} + \vec{F}_k | |||
\to | |||
\left\{ | |||
\begin{array}{lr} | |||
-10m_0R\dot{\theta}^2 = -10m_0g\,\mathrm{sen}\,\theta - 25m_0g\cos^2\theta + N, & (1)\\ | |||
10m_0\ddot{\theta} = -10m_0g\cos\theta + 25m_0g\,\mathrm{sen}\,\theta\cos\theta. & (2) | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
De la primera ecuación obtenemos | |||
<center> | |||
<math> | |||
N = -10m_0R\dot{\theta}^2 + 10m_0g\,\mathrm{sen}\,\theta + 25m_0g\cos^2\theta. | |||
</math> | |||
</center> | |||
La velocidad de la partícula es | |||
<center> | |||
<math> | |||
\vec{v} = R\dot{\theta}\,\vec{u}_{\theta}, | |||
</math> | |||
</center> | |||
por lo que la normal puede escribirse | |||
<center> | |||
<math> | |||
N = -10m_0\dfrac{v^2}{R} + 10m_0g\,\mathrm{sen}\,\theta + 25m_0g\cos^2\theta. | |||
</math> | |||
</center> | |||
Imponiendo que sea cero cuando <math>\theta=\beta</math> obtenemos la condición | |||
<center> | |||
<math> | |||
\lambda=\sqrt{3}. | |||
</math> | |||
</center> | |||
[[Categoría:Problemas de Dinámica de la partícula]] | |||
[[Categoría:Problemas de Cinética de la partícula]] | |||
[[Categoría:Dinámica del punto material|1]] | |||
Revisión actual - 11:06 3 nov 2023
Enunciado
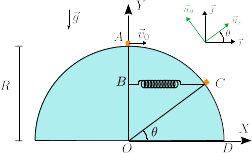
Una partícula de masa desliza sin rozamiento sobre un semidisco de radio . En el instante inicial la partícula se encuentra en el punto y se le imparte una velocidad horizontal de rapidez , siendo un número real positivo. La masa está conectada a un muelle de constante elástica y longitud natural nula. El otro extremo del muelle está conectado al punto que se mueve de modo que el muelle permanece siempre horizontal.
- Escribe los vectores de la base cartesiana en la base polar.
- Escribe la expresión de la fuerza ejercida por el muelle sobre la masa en la base polara.
- Escribe la expersión que da la velocidad de la partícula para el ángulo , con y .
- ¿Que condición debe cumplir para que la partícula se separe del disco en ese ángulo ?
Solución
Vectores cartesianos en la base polar
Observando los vectores de la base indicados en la figura del enunciado tenemos
Fuerza ejercida por el muelle
Dado que tiene longitud natural nula la fuerza ejercida por el muelle puede escribirse
Tenemos
Utilizando la expresión de del apartado anterior tenemos
Expresión de la velocidad de la partícula
Como el vínculo es liso, las únicas fuerzas que hacen trabajo son las debidas a la gravedad y al muelle, que son conservativas. Por tanto la energía mecánica se conserva. En el punto vale
Hemos escogido como altura de referencia para la energía potencial la de la base del semidisco. Para el ángulo tenemos
Evaluando para e igualando las dos expresiones obtenemos
Condición para que la partícula se separe de la superficie
Cuando la partícula se separa la normal que ejerce la superficie sobre ella se anula, pues ya no es necesaria para que la partícula no penetre en el disco. Las fuerzas que actúan sobre la partícula son, en la base polar
La aceleración de la partícula es
A partir de la Segunda Ley de Newton obtenemos
De la primera ecuación obtenemos
La velocidad de la partícula es
por lo que la normal puede escribirse
Imponiendo que sea cero cuando obtenemos la condición

























