Segunda Convocatoria Ordinaria 2014/15 (G.I.C.)

Partícula sobre rampa con muelle, tirada por un cable

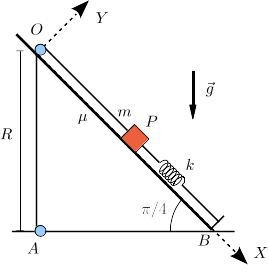
Una partícula de masa $m$ sube deslizándose por un plano inclinado bajo la acción de un cable que tire de ella. El contacto con el plano es rugoso y está caracterizado por un coeficiente de rozamiento dinámico $\mu$. El plano inclinado forma un ángulo de $\pi /4$ radianes con la horizontal. El cable gira sin rozamiento en una polea sin masa situada en el punto $A$ y se enrolla en un cilindro en el punto $O$, también sin rozamiento. Tanto la polea como el cilindro tienen radios despreciables. Además un muelle de longitud natural nula, constante elástica $k$ y anclado en el punto $B$ está acoplado a la partícula. La longitud total del cable entre los puntos $A$ y $P$ es una función del tiempo $l(t)=R+{\sqrt {2}}R(1-t/T)$, siendo $T$ una constante con dimensiones de tiempo.

1. Determina en función del tiempo los vectores posición, velocidad y aceleración de la partícula tomando como referencia el punto $O$ y los ejes cartesianos indicados en la figura.
2. Dibuja el diagrama de cuerpo libre de la partícula.
3. Calcula la fuerza ${\vec {F}}$ que ejerce el cable sobre la partícula en cada instante de tiempo.
4. Calcula el trabajo realizado por el cable y por el muelle en el trayecto entre los puntos $B$ y $O$, así como la variación de energía mecánica de la partícula.

Disco apoyado en barra y caja

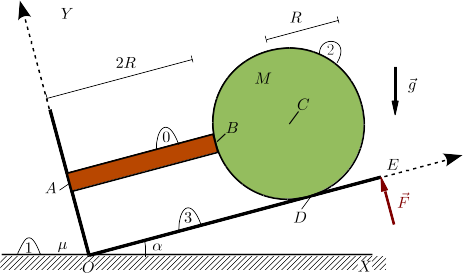
El disco de la figura tiene masa $M$ y radio $R$. Se apoya en el punto $B$ en una barra de masa despreciable y longitud $2R$, y en el punto $D$ en una caja de masa despreciable. Los contactos en $B$ y $D$ son lisos. A su vez la barra se apoya sobre la caja en el punto $A$, con contacto también liso. La caja se apoya en el suelo en el punto $O$, con un contacto rugoso caracterizado por un coeficiente de rozamiento estático $\mu$. Se aplica una fuerza ${\vec {F}}$ sobre el punto $E$ de la caja con la dirección y sentido indicados en la figura.

1. Dibuja los diagramas de cuerpo libre de la caja, el disco y la barra, indicando todas las relaciones entre las distintas fuerzas.
2. Calcula el valor de ${\vec {F}}$ para que la caja esté en equilibrio para un valor dado de $\alpha$.
3. Calcula la reacción en el punto $O$ y analiza el equilibrio frente a deslizamiento para el caso $\alpha =\pi /4$.
4. Calcula la fuerza que el disco ejerce sobre la barra y la caja para el caso $\alpha =\pi /4$.