Diferencia entre revisiones de «No Boletín - Ejemplo de movimiento circular no uniforme (Ex.Sep/11)»
(Página creada con «==Enunciado== 200px|right Una partícula de masa <math>m</math> describe un movimiento circular de radio <math>R</math>, tal que su velocidad angular instantánea cumple <center><math>\omega = k\theta\,</math></center> con <math>k</math> una constante y <math>\theta</math> el ángulo que el vector de posición instantánea forma con el eje OX. # Determine la aceleración angular de la partícula como función del ángulo <m…») |
Sin resumen de edición |
||
| Línea 16: | Línea 16: | ||
# Halle el trabajo que se realiza sobre la partícula entre esos dos puntos. | # Halle el trabajo que se realiza sobre la partícula entre esos dos puntos. | ||
--> | --> | ||
==Aceleración angular== | |||
Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular | |||
<center><math>\alpha = \dot{\omega} = k\dot{\theta}</math></center> | |||
debemos escribir <math>\dot{\theta}</math> como función del propio ángulo <math>\theta</math>, como nos pide el enunciado. Esto lo hacemos simplemente observando que la derivada temporal del ángulo girado no es otra que la velocidad angular | |||
<center><math>\dot{\theta} = \frac{\mathrm{d}\theta}{\mathrm{d}t} = \omega = k\theta</math></center> | |||
así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida | |||
<center><math>\alpha = k^2\theta\,</math></center> | |||
En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro | |||
<center><math>\vec{\alpha} = \alpha\vec{k} = k^2\theta\vec{k}</math></center> | |||
==Componentes intrínsecas de la aceleración== | |||
Tenemos dos componentes intrínsecas de la aceleración: | |||
===Aceleración tangencial=== | |||
Puesto que el movimiento no es uniforme, existe una aceleración tangencial igual a la derivada temporal de la rapidez | |||
<center><math>a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}</math></center> | |||
siendo el módulo de la velocidad | |||
<center><math>|\vec{v}| = \omega R = kR\theta</math></center> | |||
Derivando respecto al tiempo | |||
<center><math>a_t = kR \dot{\theta}= kR\omega = k^2R\theta</math></center> | |||
===Aceleración normal=== | |||
El valor de la aceleración normal es | |||
<center><math>a_n = \frac{|\vec{v}|^2}{R} = \frac{(kR\theta)^2}{R} = k^2R\theta^2</math></center> | |||
<!-- | |||
==Fuerza sobre la partícula== | |||
La fuerza sobre la partícula, por la segunda ley de Newton es igual a | |||
<center><math>\vec{F} = m\vec{a}= m\left(a_t\vec{T}+a_n\vec{N}\right)</math></center> | |||
===En θ = π/2=== | |||
En <math>\theta =\pi/2</math> las componentes intrínsecas de la aceleración, según calculamos antes, valen | |||
<center><math>a_t = \frac{k^2 R \pi}{2}\qquad a_n = k^2 R\left(\frac{\pi}{2}\right)^2 = \frac{\pi^2 k^2 R}{4}</math></center> | |||
El vector tangente es el unitario en la dirección de avance de la trayectoria, que en esta posición coincide con | |||
<center><math>\vec{T}=-\vec{\imath}</math></center> | |||
En un movimiento circular, el vector normal es el unitario radial hacia adentro de la circunferencia, que en <math>\theta = \pi/2</math> equivale a | |||
<center><math>\vec{N}=-\vec{\jmath}</math></center> | |||
Por tanto, la fuerza aplicada en este punto es igual a | |||
<center><math>\vec{F}(\theta=\pi/2) = m\left(\left(\frac{k^2 R \pi}{2}\right)(-\vec{\imath})+\left(\frac{k^2 R \pi^2}{4}\right)(-\vec{\jmath})\right) = -\frac{mk^2R\pi}{4}\left(2\vec{\imath}+\pi\vec{\jmath}\right)</math></center> | |||
<center>[[Archivo:particula-circunferencia-TN.png]]</center> | |||
===En θ = π=== | |||
Operando del mismo modo, quedan las componentes intrínsecas | |||
<center><math>a_t = k^2 R \pi\qquad a_n = k^2 R\pi^2</math></center> | |||
El vector tangente apunta ahora en la direcció y sentido del eje OY negativo | |||
<center><math>\vec{T}=-\vec{\jmath}</math></center> | |||
mientras que el vector normal es en la dirección del X positivo | |||
<center><math>\vec{N}=\vec{\imath}</math></center> | |||
Esto nos da la fuerza aplicada en este punto | |||
<center><math>\vec{F}(\theta=\pi) = m\left(\left(k^2 R \pi\right)(-\vec{\jmath})+\left(k^2 R \pi^2\right)(\vec{\imath})\right) = mk^2R\pi\left(\pi\vec{\imath}-\vec{\jmath}\right)</math></center> | |||
==Trabajo sobre la partícula== | |||
De acuerdo con el teorema de las fuerzas vivas (o teorema trabajo-energía cinética) el trabajo realizado sobre una partícula entre dos puntos es igual al incremento de su energía cinética | |||
<center><math>W = \Delta K = K_f - K_i = \frac{1}{2}m|\vec{v}_f|^2-\frac{1}{2}m|\vec{v}_i|^2</math></center> | |||
La celeridad en los dos puntos indicados vale | |||
<center><math>|\vec{v}|(\theta=\pi/2) = \frac{kR\pi}{2}\qquad\qquad |\vec{v}|(\theta=\pi) = kR\pi</math></center> | |||
lo que nos da un trabajo | |||
<center><math>W= \frac{mk^2R^2\pi^2}{2}-\frac{mk^2R^2\pi^2}{8} = \frac{3mk^2R^2\pi^2}{8}</math></center> | |||
--> | |||
[[Categoría:Problemas de Cinemática del Punto (GITI)]] | |||
Revisión actual - 22:05 9 ene 2024
Enunciado
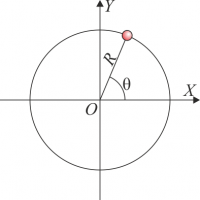
Una partícula de masa describe un movimiento circular de radio , tal que su velocidad angular instantánea cumple
con una constante y el ángulo que el vector de posición instantánea forma con el eje OX.
- Determine la aceleración angular de la partícula como función del ángulo .
- Halle las componentes intrínsecas de la aceleración lineal.
Aceleración angular
Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular
debemos escribir como función del propio ángulo , como nos pide el enunciado. Esto lo hacemos simplemente observando que la derivada temporal del ángulo girado no es otra que la velocidad angular
así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida
En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro
Componentes intrínsecas de la aceleración
Tenemos dos componentes intrínsecas de la aceleración:
Aceleración tangencial
Puesto que el movimiento no es uniforme, existe una aceleración tangencial igual a la derivada temporal de la rapidez
siendo el módulo de la velocidad
Derivando respecto al tiempo
Aceleración normal
El valor de la aceleración normal es













