No Boletín - Cálculo de distancia entre dos rectas

Enunciado

Sean las rectas $r_{1}$, que pasa por los puntos $A(-2,5,1)$ y $B(7,-7,1)$, y $r_{2}$ que pasa por $C(5,4,-3)$ y $D(5,4,2)$ (todas las unidades en el SI). Empleando el álgebra vectorial, determine la distancia entre estas dos rectas.

Solución

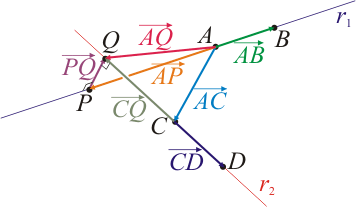
La distancia entre dos rectas es la correspondiente a la que hay entre los puntos más próximos de una y de otra. Estos dos puntos se encuentran sobre la perpendicular común a ambas rectas.

Se trata entonces de hallar la distancia entre dos puntos $P$ y $Q$ tales que $P$ pertenece a $r_{1}$, $Q$ pertenece a $r_{2}$ y ${\overrightarrow {PQ}}$ es ortogonal a los vectores directores de ambas rectas.

Si $P$ pertenece a la recta $r_{1}$, se cumple

${\overrightarrow {AP}}=\lambda \,{\overrightarrow {AB}}$

y si $Q$ pertenece a $r_{2}$

${\overrightarrow {CQ}}=\mu \,{\overrightarrow {CD}}$

El vector de posición relativo entre ambos puntos será

${\overrightarrow {PQ}}={\overrightarrow {AQ}}-{\overrightarrow {AP}}={\overrightarrow {AC}}+{\overrightarrow {CQ}}-{\overrightarrow {AP}}={\overrightarrow {AC}}+\mu \,{\overrightarrow {CD}}-\lambda \,{\overrightarrow {AB}}$

Este vector debe ser ortogonal tanto al vector ${\overrightarrow {AB}}$ como al vector ${\overrightarrow {CD}}$ y por tanto será paralelo al producto vectorial de ambos

${\overrightarrow {PQ}}=\nu \,({\overrightarrow {AB}}\times {\overrightarrow {CD}})$

La distancia entre las rectas será el módulo de este vector

$d=|{\overrightarrow {PQ}}|=|\nu |\left|{\overrightarrow {AB}}\times {\overrightarrow {CD}}\right|$

Por tanto, solo necesitamos hallar el parámetro $\nu$. Igualando las dos expresiones para el vector ${\overrightarrow {PQ}}$

$\nu \,({\overrightarrow {AB}}\times {\overrightarrow {CD}})={\overrightarrow {AC}}+\mu \,{\overrightarrow {CD}}-\lambda \,{\overrightarrow {AB}}$

Multiplicando escalarmente por ${\overrightarrow {AB}}\times {\overrightarrow {CD}}$ nos queda simplemente

$\nu \,\left|{\overrightarrow {AB}}\times {\overrightarrow {CD}}\right|^{2}={\overrightarrow {AC}}\cdot ({\overrightarrow {AB}}\times {\overrightarrow {CD}})$

y por tanto la distancia que buscamos es

$d={\frac {\left|{\overrightarrow {AC}}\cdot ({\overrightarrow {AB}}\times {\overrightarrow {CD}})\right|}{\left|{\overrightarrow {AB}}\times {\overrightarrow {CD}}\right|}}$

Nótese que el resultado final no requiere localizar los puntos $P$ y $Q$ sino que hemos llegado a una expresión para la distancia que solo depende de los cuatro puntos dados.

Sustituyendo los valores tenemos

${\overrightarrow {AB}}=(9{\vec {\imath }}-12{\vec {\jmath }})\,\mathrm {m} \,;$        ${\overrightarrow {CD}}=5{\vec {k}}\,\mathrm {m} \,;$        ${\overrightarrow {AC}}=(7{\vec {\imath }}-{\vec {\jmath }}-4{\vec {k}})\,\mathrm {m}$

Hallando los productos vectoriales y mixto

${\overrightarrow {AB}}\times {\overrightarrow {CD}}=\left(-60{\vec {\imath }}-45{\vec {\jmath }}\right)\,\mathrm {m} ^{2}\,;$        $\left|{\overrightarrow {AB}}\times {\overrightarrow {CD}}\right|=75\,\mathrm {m} ^{2}\,;$        ${\overrightarrow {AC}}\cdot ({\overrightarrow {AB}}\times {\overrightarrow {CD}})=-375\,\mathrm {m} ^{3}$

por lo que la distancia entre las rectas es

$d=\left|{\frac {-375\,\mathrm {m} ^{3}}{75\,\mathrm {m} ^{2}}}\right|=5\,\mathrm {m}$