Diferencia entre las páginas «Momento de inercia de un sólido compuesto de cuatro barras y un aro» y «Tensor de inercia de un hexágono (Dic. 2020)»
(Página creada con «= Enunciado = right El sólido de la figura está compuesto de un aro delgado de masa <math>m</math> y radio <math>R</math>, así como de cuatro barras delgadas, cada una de masa <math>m</math> y longitud <math>R</math>, dispuestas como se indica en la figura. Todos los cuerpos son homogéneos. #Calcula el momento de inercia <math>I_{zz}</math>. #Calcula el tensor de inercia en <math>O</math> expresado en los ejes cartesianos de la figura…») |
(Página creada con «= Enunciado = right EL sólido rígido de la figura es un hexágono de lado <math>L</math>. Cada lado del hexágono tiene una masa <math>m</math>. #Calcula el tensor de inercia del hexágono en su centro, expresado en los ejes de la figura.. #Calcula el tensor de inercia en el vértice <math>A</math>, expresado en los mismos ejes. #Calcula el momento de inercia respecto a un eje paralelo al eje <math>OX</math> y qu…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | = Enunciado = | ||
[[ | [[Archivo:MRGIC-tensorInerciaHexagono-enunciado.png|right]] | ||
EL sólido rígido de la figura es un hexágono de lado <math>L</math>. Cada lado del hexágono tiene una masa <math>m</math>. | |||
#Calcula el tensor de inercia del hexágono en su centro, expresado en los ejes de la figura.. | |||
#Calcula el tensor de inercia en el vértice <math>A</math>, expresado en los mismos ejes. | |||
#Calcula el | #Calcula el momento de inercia respecto a un eje paralelo al eje <math>OX</math> y que pase por <math>A</math>. | ||
#Calcula el tensor de inercia en <math> | |||
#Calcula el momento de inercia respecto al eje <math> | |||
= Solución = | = Solución = | ||
== | == Tensor de inercia en <math>O</math> == | ||
Al ser un sólido plano el eje perpendicular a el es Eje Principal de Inercia (EPI) en todos los puntos del plano del sólido. En este caso ese eje es el <math>Z</math>. Además, los ejes <math>X</math> e <math>Y</math> son ejes de simetría, por lo que también son EPI. Aunque en este caso, debido a la simetría del hexágono, todos los ejes que pasan por <math>O</math> y están contenidos en el plano <math>XY</math> son EPI. | |||
Entonces el tensor de inercia en <math>O</math> es diagonal cuando se expresa en los ejes de la figura | |||
<center> | <center> | ||
<math> | <math> | ||
I_{ | \overleftrightarrow{I_O} | ||
= | |||
\left[ | |||
\begin{array}{ccc} | |||
I_{xx} & 0 & 0 \\ | |||
0 & I_{yy} & 0 \\ | |||
0 & 0 & I_{zz} | |||
\end{array} | |||
\right]. | |||
</math> | </math> | ||
</center> | </center> | ||
Por la simetría en el plano <math>XY</math>, se tiene <math>I_{xx}=I_{yy}</math>. Y usando el Teorema de los Ejes Perpendiculares tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
I_{zz} = | I_{zz} = I_{xx} + I_{yy} = 2I_{xx} \to | ||
I_{xx} = I_{yy} = I_{zz}/2. | |||
</math> | </math> | ||
</center> | </center> | ||
Con lo cual el tensor queda | |||
<center> | <center> | ||
<math> | <math> | ||
\overleftrightarrow{I_O} | |||
= | = | ||
\dfrac{1}{3} | \left[ | ||
\begin{array}{ccc} | |||
I_{zz}/2 & 0 & 0 \\ | |||
0 & I_{zz}/2 & 0 \\ | |||
0 & 0 & I_{zz} | |||
\end{array} | |||
\right]. | |||
</math> | |||
</center> | |||
Para calcular <math>I_{zz}(O)</math> dividimos la integral en seis partes, una por cada barra. Tenemos así | |||
<center> | |||
<math> | |||
I_{zz}(O) = 6I_b(O), | |||
</math> | |||
</center> | |||
[[Archivo:MRGIC-tensorInerciaHexagono-triangulo.png|right]] | |||
Donde <math>I_b(O)</math> es el momento de inercia de cada barra respecto a un eje paralelo a <math>Z</math> que pasa por <math>O</math>. Por la simetría del hexágono esta magnitud es la misma para las seis barras. El hexágono se puede dividir en seis triángulos equiláteros de lado <math>L</math>, como se indica en la figura. Utilizando el Teorema de los Ejes Paralelos tenemos | |||
<center> | |||
<math> | |||
I_b(O) = I_{zz}(C) + mh^2 | |||
</math> | |||
</center> | |||
El momento <math>I_{zz}(C)</math> es el momento de inercia de la varilla respecto a un eje perpendicular a ella que pasa por su centro, esto es | |||
<center> | |||
<math> | |||
I_{zz}(C) = mL^2/12. | |||
</math> | |||
</center> | |||
De la figura tenemos | |||
<center> | |||
<math> | |||
h = \sqrt{L^2 - L^2/4} = \sqrt{3}L/2. | |||
</math> | |||
</center> | |||
Por tanto | |||
<center> | |||
<math> | |||
I_b(O) = \dfrac{1}{12}mL^2 + \dfrac{3}{4}mL^2 = \dfrac{5}{6}mL^2. | |||
</math> | </math> | ||
</center> | </center> | ||
Y para todo el hexágono | |||
<center> | <center> | ||
<math> | <math> | ||
I_{zz}(O) = 6I_b(O) = 5mL^2. | |||
</math> | </math> | ||
</center> | </center> | ||
Y el tensor que se pide es | |||
<center> | <center> | ||
<math> | <math> | ||
\overleftrightarrow{I_O} | |||
= | |||
\left[ | |||
\begin{array}{ccc} | |||
5mL^2/2 & 0 & 0 \\ | |||
0 & 5mL^2/2 & 0 \\ | |||
0 & 0 & 5mL^2 | |||
\end{array} | |||
\right]. | |||
</math> | </math> | ||
</center> | </center> | ||
== Tensor de inercia en <math> | == Tensor de inercia en <math>A</math> == | ||
Utilizamos el Teorema de Steiner para trasladar el tensor de inercia desde <math>O</math> hasta <math>A</math>: | |||
<center> | |||
<math> | |||
\overleftrightarrow{I_A} | |||
= | |||
\overleftrightarrow{I_O} | |||
+ | |||
m\left(|\overrightarrow{OA}|^2 \overleftrightarrow{U} - \overrightarrow{OA}\,\overrightarrow{OA}\right). | |||
\begin{array}{c}\end{array} | |||
</math> | |||
</center> | |||
Tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\overrightarrow{OA} = | |||
L\,(\cos(\pi/3)\,\vec{\imath}+ \mathrm{sen}\,(\pi/3)\,\vec{\jmath}) | |||
= | |||
L\,\left(\dfrac{1}{2}\,\vec{\imath}+ \dfrac{\sqrt{3}}{2}\,\vec{\jmath}\right) | |||
</math> | </math> | ||
</center> | </center> | ||
Operando | |||
<center> | <center> | ||
<math> | <math> | ||
|\overrightarrow{OA}|^2\overleftrightarrow{U} | |||
= | |||
\left[ | |||
\begin{array}{ccc} | |||
L^2 & 0 & 0 \\ | |||
0 & L^2 & 0 \\ | |||
0 & 0 & L^2 | |||
\end{array} | |||
\right], | |||
\qquad | |||
\overrightarrow{OA}\,\overrightarrow{OA} | |||
= | |||
\left[ | |||
\begin{array}{ccc} | |||
L^2/4 & \sqrt{3}L^2/4 & 0 \\ | |||
\sqrt{3}L^2/4 & 3L^2/4 & 0 \\ | |||
0 & 0 & 0 | |||
\end{array} | |||
\right]. | |||
</math> | </math> | ||
</center> | </center> | ||
El término que se añade al tensor en <math>O</math> es | |||
<center> | <center> | ||
<math> | <math> | ||
\left[ | |||
\begin{array}{ccc} | |||
3mL^2/4 & -m\sqrt{3}L^2/4 & 0 \\ | |||
-m\sqrt{3}L^2/4 & mL^2/4 & 0 \\ | |||
0 & 0 & mL^2 | |||
\end{array} | |||
\right]. | |||
</math> | </math> | ||
</center> | </center> | ||
Y el resultado pedido es | |||
<center> | <center> | ||
<math> | <math> | ||
\overleftrightarrow{ | \overleftrightarrow{I_A} | ||
= | = | ||
\left[ | \left[ | ||
\begin{array}{ccc} | \begin{array}{ccc} | ||
13mL^2/4 & -m\sqrt{3}L^2/4 & 0 \\ | |||
-m\sqrt{3}L^2/4 & 11mL^2/4 & 0 \\ | |||
0 & 0 & 2 | 0 & 0 & 6mL^2 | ||
\end{array} | \end{array} | ||
\right] | \right]. | ||
</math> | </math> | ||
</center> | </center> | ||
Podemos observar que el Teorema de los Ejes perpendiculares se sigue cumpliendo en este tensor, como debe ser pues es un sólido plano. | |||
También vemos que el tensor en <math>A</math> no es diagonal. Esto significa que los ejes <math>X</math> e <math>Y</math> no son EPI en <math>A</math>. | |||
== Momento de inercia respecto a <math>\ | == Momento de inercia en <math>A</math> == | ||
Una vez calculado el tensor de inercia en <math>A</math> podemos calcular el momento de inercia respecto a un eje que pase por <math>A</math> si tenemos un vector unitario en la dirección de ese eje | |||
<center> | |||
<math> | |||
I(A) = \vec{n}\cdot\overleftrightarrow{I_A}\cdot\vec{n}. | |||
\begin{array}{c}\end{array} | |||
</math> | |||
</center> | |||
En este caso el vector adecuado es | |||
<center> | <center> | ||
<math> | <math> | ||
\vec{n} = \vec{\imath} = [1,0,0]. | |||
</math> | </math> | ||
</center> | </center> | ||
Operando tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
I_{\ | I_{xx}(A) = | ||
[1,0,0]\left[ | |||
\begin{array}{ccc} | |||
13mL^2/4 & -m\sqrt{3}L^2/4 & 0 \\ | |||
-m\sqrt{3}L^2/4 & 11mL^2/4 & 0 \\ | |||
0 & 0 & 6mL^2 | |||
\end{array} | |||
\right] | |||
\left[ | |||
\begin{array}{c} | |||
1\\0\\0 | |||
\end{array} | |||
\right] | |||
= 13mL^2/4. | |||
</math> | </math> | ||
</center> | </center> | ||
[[Categoría:Problemas de cinética del sólido rígido]] | [[Categoría:Problemas de cinética del sólido rígido]] | ||
[[Categoría:Problemas de dinámica del sólido rígido (MR)]] | |||
[[Categoría:Problemas de dinámica del sólido rígido]] | |||
[[Categoría:Problemas de dinámica del sólido rígido (MR)]] | |||
[[Categoría:Problemas de examen de Mecánica Racional]] | [[Categoría:Problemas de examen de Mecánica Racional]] | ||
Revisión actual - 16:51 17 oct 2023
Enunciado
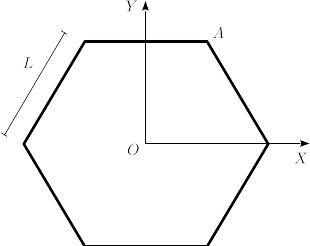
EL sólido rígido de la figura es un hexágono de lado . Cada lado del hexágono tiene una masa .
- Calcula el tensor de inercia del hexágono en su centro, expresado en los ejes de la figura..
- Calcula el tensor de inercia en el vértice , expresado en los mismos ejes.
- Calcula el momento de inercia respecto a un eje paralelo al eje y que pase por .
Solución
Tensor de inercia en
Al ser un sólido plano el eje perpendicular a el es Eje Principal de Inercia (EPI) en todos los puntos del plano del sólido. En este caso ese eje es el . Además, los ejes e son ejes de simetría, por lo que también son EPI. Aunque en este caso, debido a la simetría del hexágono, todos los ejes que pasan por y están contenidos en el plano son EPI.
Entonces el tensor de inercia en es diagonal cuando se expresa en los ejes de la figura
Por la simetría en el plano , se tiene . Y usando el Teorema de los Ejes Perpendiculares tenemos
Con lo cual el tensor queda
Para calcular dividimos la integral en seis partes, una por cada barra. Tenemos así
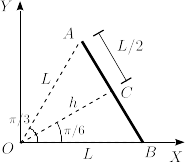
Donde es el momento de inercia de cada barra respecto a un eje paralelo a que pasa por . Por la simetría del hexágono esta magnitud es la misma para las seis barras. El hexágono se puede dividir en seis triángulos equiláteros de lado , como se indica en la figura. Utilizando el Teorema de los Ejes Paralelos tenemos
El momento es el momento de inercia de la varilla respecto a un eje perpendicular a ella que pasa por su centro, esto es
De la figura tenemos
Por tanto
Y para todo el hexágono
Y el tensor que se pide es
Tensor de inercia en
Utilizamos el Teorema de Steiner para trasladar el tensor de inercia desde hasta :
Tenemos
Operando
El término que se añade al tensor en es
Y el resultado pedido es
Podemos observar que el Teorema de los Ejes perpendiculares se sigue cumpliendo en este tensor, como debe ser pues es un sólido plano. También vemos que el tensor en no es diagonal. Esto significa que los ejes e no son EPI en .
Momento de inercia en
Una vez calculado el tensor de inercia en podemos calcular el momento de inercia respecto a un eje que pase por si tenemos un vector unitario en la dirección de ese eje
En este caso el vector adecuado es
Operando tenemos









![{\displaystyle {\overleftrightarrow {I_{O}}}=\left[{\begin{array}{ccc}I_{xx}&0&0\\0&I_{yy}&0\\0&0&I_{zz}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/feaf4cca44318e261e5bf8487fa7040afe2d3bc0)


![{\displaystyle {\overleftrightarrow {I_{O}}}=\left[{\begin{array}{ccc}I_{zz}/2&0&0\\0&I_{zz}/2&0\\0&0&I_{zz}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8996aef863860c1a8838ed8dfffed1ad40585269)









![{\displaystyle {\overleftrightarrow {I_{O}}}=\left[{\begin{array}{ccc}5mL^{2}/2&0&0\\0&5mL^{2}/2&0\\0&0&5mL^{2}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0aced418773e063ba19055297f4c097b62d22e6)


![{\displaystyle |{\overrightarrow {OA}}|^{2}{\overleftrightarrow {U}}=\left[{\begin{array}{ccc}L^{2}&0&0\\0&L^{2}&0\\0&0&L^{2}\end{array}}\right],\qquad {\overrightarrow {OA}}\,{\overrightarrow {OA}}=\left[{\begin{array}{ccc}L^{2}/4&{\sqrt {3}}L^{2}/4&0\\{\sqrt {3}}L^{2}/4&3L^{2}/4&0\\0&0&0\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c1782c329cb6f62d68a58ee39a2c2dc0893aff)
![{\displaystyle \left[{\begin{array}{ccc}3mL^{2}/4&-m{\sqrt {3}}L^{2}/4&0\\-m{\sqrt {3}}L^{2}/4&mL^{2}/4&0\\0&0&mL^{2}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c9d59df5a4fcdac99c93f9e0eaac3040a03b02b)
![{\displaystyle {\overleftrightarrow {I_{A}}}=\left[{\begin{array}{ccc}13mL^{2}/4&-m{\sqrt {3}}L^{2}/4&0\\-m{\sqrt {3}}L^{2}/4&11mL^{2}/4&0\\0&0&6mL^{2}\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8848eb3f61438b81233c87985c7e01b40053bd49)

![{\displaystyle {\vec {n}}={\vec {\imath }}=[1,0,0].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9dc3eb668ce75db33ab66232a057787f7a7a334)
![{\displaystyle I_{xx}(A)=[1,0,0]\left[{\begin{array}{ccc}13mL^{2}/4&-m{\sqrt {3}}L^{2}/4&0\\-m{\sqrt {3}}L^{2}/4&11mL^{2}/4&0\\0&0&6mL^{2}\end{array}}\right]\left[{\begin{array}{c}1\\0\\0\end{array}}\right]=13mL^{2}/4.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd0d0c679d5762eccab24296f81975945f088f51)