Diferencia entre las páginas «Partícula sometida a la acción de dos muelles (GIA)» y «Partícula en un tubo que gira con velocidad angular constante (GIA)»
Secciones
(Página creada con «== Enunciado == right Una partícula <math>P</math>, de masa <math>m</math>, se mueve en el plano horizontal sometida a la acción de dos resortes elásticos ideales e idénticos, de constante <math>k</math> y longitud natural nula. Los puntos de anclaje son <math>C(-d,0)</math> y <math>D(d,0)</math>, respectivamente #Escribe la ecuación diferencial que determina el movimiento de la partícula. #Si las condiciones iniciale…») |
(Página creada con «== Enunciado == Una partícula de masa <math>m</math> se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme <math>\omega</math> en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede describirse como <center><math> \begin{matrix} x(t) = r(t)\,\cos(\omega t)&\qquad\qquad& y(t) = r(t)\,\,\mathrm{sen}\,(\omega t) \end{matrix} </math></center> #Halla la ecuación diferencial que cumple la fu…») |
||
| Línea 1: | Línea 1: | ||
== Enunciado == | == Enunciado == | ||
Una partícula de masa <math>m</math> se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme <math>\omega</math> en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede describirse como | |||
Una partícula | <center><math> | ||
\begin{matrix} | |||
# | x(t) = r(t)\,\cos(\omega t)&\qquad\qquad& y(t) = r(t)\,\,\mathrm{sen}\,(\omega t) | ||
# | \end{matrix} | ||
</math></center> | |||
#Halla la ecuación diferencial que cumple la función <math>r(t)</math> sabiendo que el vínculo entre la partícula y el tubo es liso. | |||
#Comprueba que | |||
<center><math> | |||
r(t) = A\,e^{\omega t} | |||
</math></center> | |||
es una solución de la ecuación para <math>r(t)</math>. | |||
#Para esta solución particular | |||
##Calcula la fuerza ejercida por el tubo en cada instante. | |||
##Halla la potencia desarrollada por el tubo sobre la partícula. Calcula el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de <math>r=b</math> a <math>r=2b</math>. | |||
##Calcula el incremento de la energía cinética de la partícula en el mismo intervalo u comprueba que se verifica el teorema de las fuerzas vivas o de la energía. | |||
== Solución == | == Solución == | ||
La | === Ecuaciones de movimiento === | ||
<center><math> | |||
[[Imagen:F1_GIA_tubo_rotando_fuerza.png|right]] | |||
</math></center> | |||
donde, <math> | La ecuación de movimiento es la Segunda Ley de Newton | ||
<center> | |||
<math> | |||
m\,\vec{a} = \sum\limits_{i=1}^n\vec{F}_i + \sum\limits_{j=i}^s\vec{\Phi}_j | |||
</math> | |||
</center> | |||
donde <math>\vec{F}_i </math> son las fuerzas activas y <math>\vec{\Phi}_j </math> son las fuerzas de reacción vincular | |||
que actúan sobre las partículas. | |||
En este problema no hay fuerzas activas, pues no se habla del peso. La única fuerza que actúa sobre la partícula | |||
es la fuerza de reacción vincular, <math>\vec{\Phi} </math>, que ejerce sobre ella el tubo cuando gira, obligándola a permanecer dentro de él. | |||
El enunciado dice que el vínculo es liso. Esto quiere decir que <math>\vec{\Phi} </math> es perpendicular al tubo. | |||
Por tanto la segunda Ley de Newton queda | |||
<center> | |||
<math> | |||
m\,\vec{a} = \vec{\Phi} | |||
</math> | |||
</center> | |||
Vamos a resolver el problema usando coordenadas polares. En estas coordenadas los vectores de posición, velocidad y | |||
aceleración son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{r} = \rho\,\vec{u}_{\rho} \\ \\ | |||
\vec{v} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta} \\ \\ | |||
\vec{a} = (\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta})\,\vec{u}_{\theta} | |||
\end{array} | |||
</math> | |||
</center> | |||
{{ac|Coordenadas polares}} | |||
En este problema la partícula está obligada a permanecer dentro del tubo, y este gira con velocidad angular constante | |||
<math>\omega </math>. Por tanto, la variación del ángulo <math> \theta </math> con el tiempo es | |||
<center> | |||
<math> | |||
\theta(t) = \omega\,t | |||
</math> | |||
</center> | |||
Hemos tomado <math>\theta(0)=0 </math> para simplificar. Por tanto, en este caso las expresiones de la posición, la | |||
velocidad y la aceleración quedan | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{r} = \rho\,\vec{u}_{\rho} \\ \\ | |||
\vec{v} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\omega\,\vec{u}_{\theta} \\ \\ | |||
\vec{a} = (\ddot{\rho}-\rho\,\omega^2)\,\vec{u}_{\rho} + 2\,\dot{\rho}\,\omega\,\vec{u}_{\theta} | |||
\end{array} | |||
</math> | |||
</center> | |||
La expresión de la fuerza de reacción vincular en coordenadas polares, al ser perpendicular al tubo, es | |||
<center> | |||
<math> | |||
\vec{\Phi} = \Phi\,\vec{u}_{\theta} | |||
</math> | |||
</center> | |||
La Segunda Ley de Newton, que es una ecuación vectorial, da lugar en este caso a dos ecuaciones escalares, | |||
una por cada componente | |||
<center> | |||
<math> | |||
m\vec{a} = \vec{\Phi} \rightarrow | |||
\left\{ | |||
\begin{array}{lcl} | |||
\vec{u}_{\rho} & \to & m(\ddot{\rho}-\rho\,\omega^2)=0 \\ & & \\ | |||
\vec{u}_{\theta} & \to & 2\,m\,\dot{\rho}\,\omega = \Phi | |||
\end{array} | |||
\right. | |||
</math> | |||
</center> | |||
Resolviendo la primera ecuación obtenemos <math>\rho(t) </math>. Una vez conocida esta, la segunda ecuación | |||
nos da la expresión de la fuerza de reacción vincular <math>\Phi(t) </math>. | |||
=== Resolución de la ecuación diferencial === | |||
==== Solución general ==== | |||
La ecuación diferencial para <math>\rho(t) </math> es | |||
<center> | |||
<math> | |||
\ddot{\rho} = w^2\,\rho | |||
</math> | |||
</center> | |||
Puede comprobarse que las funciones <math>e^{\omega t} </math> y <math>e^{-\omega t} </math> son solución de esta | |||
ecuación. Por tanto, la solución general es de la forma | |||
<center> | |||
<math> | |||
\rho(t) = A\,e^{\omega t} + B\,e^{\omega t} | |||
</math> | |||
</center> | |||
Las constantes <math>A </math> y <math>B </math> se determinan a partir de las condiciones iniciales. | |||
La solución general puede escribirse de una forma alternativa usando las definiciones del seno y coseno hiperbólicos | |||
<center> | |||
<math> | |||
\cosh(\alpha) = \dfrac{e^{\alpha} + e^{-\alpha}}{2} \qquad\qquad \mathrm{senh}(\alpha) = \dfrac{e^{\alpha} - e^{-\alpha}}{2} | |||
</math> | |||
</center> | |||
De esta forma la solución general se puede escribir | |||
<center> | |||
<math> | |||
\rho(t) = a\,\cosh(\omega t) + b\,\mathrm{senh}(\omega t) | |||
</math> | |||
</center> | |||
==== Condiciones iniciales ==== | |||
Vamos a suponer que en el instante inicial el tubo es paralelo al eje <math>OX </math> y la partícula está situada | |||
a una distancia <math>\rho_0 </math> del origen. Eso nos da una condición inicial sobre la posición | |||
<center> | |||
<math> | |||
\rho(0) = \rho_0\, | |||
</math> | |||
</center> | |||
Al empezar a girar el tubo, en un primer momento la partícula gira con él, por lo que la velocidad no tiene componente | |||
radial. Así pues, | |||
<center> | |||
<math> | |||
\dot{\rho}(0)=0 | |||
</math> | |||
</center> | |||
Determinamos las constantes <math>a </math> y <math>b </math> a partir de estas condiciones iniciales | |||
<center> | |||
<math> | |||
\begin{array}{lclcl} | |||
\rho(t) = a\,\cosh(\omega t) + b\,\mathrm{senh}(\omega t) &\to& \rho(0)=a=\rho_0 &\to& a = \rho_0 \\ &&&& \\ | |||
\dot{\rho}(t) = a\,\omega\,\mathrm{senh}(\omega t) + b\,\omega\,\cosh(\omega t) &\to& \dot{\rho}(0)=b\,\omega=0 &\to& b= 0 | |||
\end{array} | |||
</math> | |||
</center> | |||
Así pues, la evolución en el tiempo de la posición de la partícula, expresada en coordenadas polares, viene dada por | |||
las funciones | |||
<center> | |||
<math> | |||
\rho(t) = \rho_0\cosh(\omega t) \qquad \qquad \theta(t) = \omega t | |||
</math> | |||
</center> | |||
==== Comportamiento asintótico ==== | |||
La función que da la evolución de la distancia de la partícula al origen puede escribirse | |||
<center> | |||
<math> | |||
\rho(t) = \rho_0\cosh(\omega t) = \dfrac{\rho_0}{2}\left(e^{\omega t} + e^{-\omega t}\right) | |||
</math> | |||
</center> | |||
<center><math> | Al aumentar el tiempo, la primera exponencial crece, mientras que la segunda decrece. Vamos a ver que en un tiempo | ||
corto esta segunda exponencial puede despreciarse respecto a la primera. | |||
</math></center> | La escala de tiempo relevante es el tiempo que tarda el tubo en dar una vuelta. Si la velocidad angular es <math>\omega </math> este tiempo es | ||
<center> | |||
<math> | |||
T = 2\pi/\omega | |||
</math> | |||
</math> | </center> | ||
Vamos a ver el valor de las exponenciales para algunos valores de t | |||
< | {| class='bordeado' | ||
! Tiempo | |||
!<math>e^{\omega t} </math> | |||
!<math>e^{-\omega t} </math> | |||
!<math>e^{-\omega t}/e^{\omega t} </math> | |||
|- | |||
|0 | |||
</math></center> | |1 | ||
|1 | |||
|1 | |||
|- | |||
|T/4 | |||
|4.81 | |||
|0.208 | |||
|0.043 | |||
|- | |||
|T/2 | |||
|23.1 | |||
|0.043 | |||
|0.0019 | |||
|} | |||
Es decir, cuando el tubo ha dado simplemente media vuelta, el valor de la segunda exponencial es sólo un 0.19% del valor | |||
de la primera. Este factor se va haciendo más pequeño. Esto quiere decir que después de media vuelta del tubo, | |||
el valor de la coordenada <math>\rho(t) </math> puede aproximarse con muy buena aproximación por | |||
<center> | |||
<math> | |||
\rho(t) \simeq \dfrac{1}{2}\rho_0\,e^{\omega t} | |||
</math> | |||
</center> | |||
=== Fuerza ejercida por el tubo === | |||
La ecuación obtenida de las componentes angulares de la Segunda Ley de Newton nos da el valor de la fuerza | |||
de reacción vincular | |||
<center> | |||
<math> | |||
\vec{\Phi} = 2\,m\,\omega\,\dot{\rho}\,\vec{u}_{\theta}\simeq m\,\rho_0\,\omega^2e^{\omega t}\,\vec{u}_{\theta} | |||
</math> | |||
</center> | |||
Hemos usado la aproximación asintótica de <math>\rho(t) </math>. | |||
=== | === Potencia desarrollada sobre la partícula === | ||
Dada una fuerza <math>\vec{\Phi} </math> actuando sobre una partícula, la potencia que le transfiere | |||
en cada instante es | |||
<center> | |||
<math> | |||
P = \vec{\Phi}\cdot\vec{v} | |||
</math> | |||
</center> | |||
En nuestro caso, usando coordenadas polares tenemos | |||
<center> | |||
<math> | |||
P = (\Phi\,\vec{u}_{\theta})\cdot(\dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta}) | |||
=\rho\,\dot{\theta}\,\Phi | |||
</math> | |||
</center> | |||
En este problema, y utilizando la expresión asintótica de <math>\rho(t) </math> tenemos | |||
<center> | |||
<math> | |||
P \simeq \dfrac{1}{2}m\,\rho_0^2\,\omega^3\,e^{2\omega t} | |||
</math> | |||
</center> | |||
=== | === Trabajo realizado sobre la partícula entre <math>\rho=b </math> y <math>\rho=2b </math> === | ||
Vamos a calcular estre trabajo de dos formas, integrando la potencia en el tiempo e integrando | |||
el trabajo a partir de su definición | |||
====Integración de la potencia ==== | |||
<center><math> | La potencia instantánea se define como | ||
<center> | |||
</math></center> | <math> | ||
P(t) = \dfrac{\mathrm{d}W}{\mathrm{d}t} \Rightarrow \mathrm{d}W = P(t)\,\mathrm{d}t | |||
</math> | |||
</center> | |||
<center><math> | Como tenemos la expresión de la potencia instantánea en función del tiempo, tenemos que hacer la integral | ||
<center> | |||
<math> | |||
W_{\rho=b}^{\rho=2b} = \int\limits_{t_b}^{t_{2b}}P(t)\,\mathrm{d}t | |||
</math> | |||
</center> | |||
donde <math>t_b </math> y <math>t_{2b} </math> son los instantes de tiempo en los cuales el valor | |||
de <math>\rho(t) </math> es <math>b </math> y <math>2b </math>, respectivamente. Para determinar | |||
estos valores usamos la expresión asintótica de <math>\rho(t) </math> | |||
< | |||
<center> | <center> | ||
<math> | <math> | ||
\begin{array}{lcl} | \begin{array}{lcl} | ||
\rho(t_b) = \dfrac{1}{2}\rho_0\,e^{\omega t_b}=b & \to & t_b = \dfrac{1}{\omega}\ln\left(\dfrac{2b}{\rho_0}\right) | |||
\\ \\ | |||
\rho(t_{2b}) = \dfrac{1}{2}\rho_0\,e^{\omega t_{2b}}=2b & \to & t_{2b} = \dfrac{1}{\omega}\ln\left(\dfrac{4b}{\rho_0}\right) | |||
\end{array} | |||
</math> | |||
</center> | |||
Ahora podemos hacer la integral | |||
<center> | |||
<math> | |||
\begin{array}{ll} | |||
W_{\rho=b}^{\rho=2b}& = \int\limits_{t_b}^{t_{2b}}P(t)\,\mathrm{d}t\\ &\\ | |||
& = \int\limits_{t_b}^{t_{2b}}\dfrac{1}{2}m\,\rho_0^2\,\omega^3\,e^{2\omega t}\,\mathrm{d}t\\ | |||
&\\ | |||
& = \dfrac{1}{2}m\,\rho_0^2\,\omega^3\int\limits_{t_b}^{t_{2b}}\,e^{2\omega t}\,\mathrm{d}t\\ | |||
&\\ | |||
& = \dfrac{1}{4}m\,\rho_0^2\,\omega^2\left[e^{2\omega t}\right]_{t_b}^{t_{2b}} | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
Tenemos | |||
<center> | |||
<math> | |||
e^{2\omega t_b} = e^{2\ln\left(2b/\rho_0\right)} = \left(e^{\ln\left(2b/\rho_0\right)}\right)^2= \left(\dfrac{2b}{\rho_0}\right)^2 | |||
</math> | |||
</center> | |||
Operando igual para <math>e^{2\omega t_{2b}} </math> obtenemos para el trabajo | |||
<center> | |||
<math> | |||
W_{\rho=b}^{\rho=2b} = 3\,m\,b^2\,\omega^2 | |||
</math> | |||
</center> | |||
==== Integración de la definición de trabajo ==== | |||
Al realizar un desplazamiento diferencial <math>\mathrm{d}\vec{r} </math> el trabajo realizado | |||
por la fuerza de reacción vincular es | |||
<center> | |||
<math> | |||
\mathrm{d}W = \vec{\Phi}\cdot\mathrm{d}\vec{r} | |||
</math> | |||
</center> | |||
El desplazamiento <math>\mathrm{d}\vec{r} </math> es | |||
<center> | |||
<math> | |||
\mathrm{d}\vec{r} = \vec{v}\,\mathrm{d}t = (\dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta})\,\mathrm{d}t | |||
</math> | |||
</center> | |||
Una derivada es un cociente entre dos incrementos muy pequeños. Podemos hacer entonces | |||
<center> | |||
<math> | |||
\dot{\rho}\,\mathrm{d}t = \dfrac{\mathrm{d}\rho}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\rho | |||
\qquad\qquad | |||
\dot{\theta}\,\mathrm{d}t = \dfrac{\mathrm{d}\theta}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\theta | |||
</math> | |||
</center> | |||
Entonces el desplazamiento diferencial se puede expresar en función de las variaciones infinitesimales de <math>\rho </math> | |||
y <math>\theta </math> | |||
<center> | |||
<math> | |||
\mathrm{d}\vec{r} = \mathrm{d}\rho\,\vec{u}_{\rho} + \rho\,\mathrm{d}\theta\,\vec{u}_{\theta} | |||
</math> | |||
</center> | |||
Entonces el trabajo realizado por la fuerza de reacción vincular en un tiempo <math>\mathrm{d}t </math> es | |||
<center> | |||
<math> | |||
\mathrm{d}W = \vec{\Phi}\cdot\mathrm{d}\vec{r} = (\Phi\,\vec{u}_{\theta})\cdot(\mathrm{d}\rho\,\vec{u}_{\rho} + \rho\,\mathrm{d}\theta\,\vec{u}_{\theta}) = \Phi\,\rho\,\mathrm{d}\theta = 2\,m\,\omega\,\rho\,\dot{\rho}\,\mathrm{d}\theta | |||
</math> | |||
</center> | |||
Utilizando otra vez la idea de que la derivada es un cociente tenemos | |||
<center> | |||
<math> | |||
\dot{\rho}\,\mathrm{d}\theta = \dfrac{\mathrm{d}\rho}{\mathrm{d}t}\,\mathrm{d}t = \mathrm{d}\rho\dfrac{\mathrm{d}\theta}{\mathrm{d}t} = | |||
\mathrm{d}\rho\,\omega | |||
</math> | |||
</center> | |||
Por tanto el trabajo infinitesimal es | |||
<center> | |||
<math> | |||
\mathrm{d}W = 2\,m\,\omega^2\,\rho\,\mathrm{d}\rho | |||
</math> | |||
</center> | |||
Ahora podemos calcular el trabajo en función del cambio en la coordenada radial | |||
<center> | |||
<math> | |||
W_{\rho=b}^{\rho=2b} = \int\limits_b^{2b}2\,m\,\omega^2\,\rho\,\mathrm{d}\rho= m\,\omega^2\,\left[\rho^2\right]_b^{2b} | |||
=3\,m\,b^2\,\omega^2 | |||
</math> | |||
</center> | |||
Obtenemos el mismo resultado que con el método anterior. | |||
=== Variación de la energía cinética === | |||
La energía cinética en cada instante es | |||
<center> | |||
<math> | |||
T = \dfrac{1}{2}m\,v^2 = \dfrac{m}{2}\left(\dot{\rho}^2+ \rho^2\dot{\theta}^2\right) | |||
\simeq | |||
\dfrac{m\,\rho_0^2\,\omega^2}{4}e^{2\omega t} | |||
</math> | |||
</center> | |||
donde hemos usado la solución asintótica. Como tenemos los instantes de tiempo que corresponden a <math>\rho=b </math> | |||
y <math>\rho=2b </math>, podemos calcular la variación de energía cinética | |||
<center> | |||
<math> | |||
\Delta T = T(t_{2b}) - T(t_b) = \dfrac{m}{2}\left(8\,b^2\,\omega^2 - 2\,b^2\,\omega^2\right) = 3\,m\,b^2\,\omega^2 | |||
</math> | |||
</center> | |||
Podemos comprobar que la variación de la energía cinética es igual al trabajo realizado por la fuerza de reacción vincular. Se | |||
verifica así el teorema de las fuerzas vivas. | |||
Revisión actual - 14:27 31 oct 2023
Enunciado
Una partícula de masa se encuentra en el interior de un tubo estrecho, el cual gira con velocidad angular uniforme en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede describirse como
- Halla la ecuación diferencial que cumple la función sabiendo que el vínculo entre la partícula y el tubo es liso.
- Comprueba que
es una solución de la ecuación para .
- Para esta solución particular
- Calcula la fuerza ejercida por el tubo en cada instante.
- Halla la potencia desarrollada por el tubo sobre la partícula. Calcula el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de a .
- Calcula el incremento de la energía cinética de la partícula en el mismo intervalo u comprueba que se verifica el teorema de las fuerzas vivas o de la energía.
Solución
Ecuaciones de movimiento
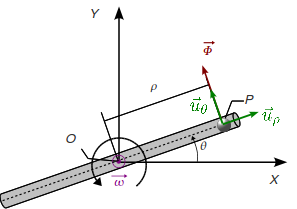
La ecuación de movimiento es la Segunda Ley de Newton
donde son las fuerzas activas y son las fuerzas de reacción vincular que actúan sobre las partículas.
En este problema no hay fuerzas activas, pues no se habla del peso. La única fuerza que actúa sobre la partícula es la fuerza de reacción vincular, , que ejerce sobre ella el tubo cuando gira, obligándola a permanecer dentro de él. El enunciado dice que el vínculo es liso. Esto quiere decir que es perpendicular al tubo. Por tanto la segunda Ley de Newton queda
Vamos a resolver el problema usando coordenadas polares. En estas coordenadas los vectores de posición, velocidad y
aceleración son
En este problema la partícula está obligada a permanecer dentro del tubo, y este gira con velocidad angular constante . Por tanto, la variación del ángulo con el tiempo es
Hemos tomado para simplificar. Por tanto, en este caso las expresiones de la posición, la velocidad y la aceleración quedan
La expresión de la fuerza de reacción vincular en coordenadas polares, al ser perpendicular al tubo, es
La Segunda Ley de Newton, que es una ecuación vectorial, da lugar en este caso a dos ecuaciones escalares, una por cada componente
Resolviendo la primera ecuación obtenemos . Una vez conocida esta, la segunda ecuación nos da la expresión de la fuerza de reacción vincular .
Resolución de la ecuación diferencial
Solución general
La ecuación diferencial para es
Puede comprobarse que las funciones y son solución de esta ecuación. Por tanto, la solución general es de la forma
Las constantes y se determinan a partir de las condiciones iniciales.
La solución general puede escribirse de una forma alternativa usando las definiciones del seno y coseno hiperbólicos
De esta forma la solución general se puede escribir
Condiciones iniciales
Vamos a suponer que en el instante inicial el tubo es paralelo al eje y la partícula está situada a una distancia del origen. Eso nos da una condición inicial sobre la posición
Al empezar a girar el tubo, en un primer momento la partícula gira con él, por lo que la velocidad no tiene componente radial. Así pues,
Determinamos las constantes y a partir de estas condiciones iniciales
Así pues, la evolución en el tiempo de la posición de la partícula, expresada en coordenadas polares, viene dada por las funciones
Comportamiento asintótico
La función que da la evolución de la distancia de la partícula al origen puede escribirse
Al aumentar el tiempo, la primera exponencial crece, mientras que la segunda decrece. Vamos a ver que en un tiempo corto esta segunda exponencial puede despreciarse respecto a la primera. La escala de tiempo relevante es el tiempo que tarda el tubo en dar una vuelta. Si la velocidad angular es este tiempo es
Vamos a ver el valor de las exponenciales para algunos valores de t
| Tiempo | |||
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| T/4 | 4.81 | 0.208 | 0.043 |
| T/2 | 23.1 | 0.043 | 0.0019 |
Es decir, cuando el tubo ha dado simplemente media vuelta, el valor de la segunda exponencial es sólo un 0.19% del valor de la primera. Este factor se va haciendo más pequeño. Esto quiere decir que después de media vuelta del tubo, el valor de la coordenada puede aproximarse con muy buena aproximación por
Fuerza ejercida por el tubo
La ecuación obtenida de las componentes angulares de la Segunda Ley de Newton nos da el valor de la fuerza de reacción vincular
Hemos usado la aproximación asintótica de .
Potencia desarrollada sobre la partícula
Dada una fuerza actuando sobre una partícula, la potencia que le transfiere en cada instante es
En nuestro caso, usando coordenadas polares tenemos
En este problema, y utilizando la expresión asintótica de tenemos
Trabajo realizado sobre la partícula entre y
Vamos a calcular estre trabajo de dos formas, integrando la potencia en el tiempo e integrando el trabajo a partir de su definición
Integración de la potencia
La potencia instantánea se define como
Como tenemos la expresión de la potencia instantánea en función del tiempo, tenemos que hacer la integral
donde y son los instantes de tiempo en los cuales el valor de es y , respectivamente. Para determinar estos valores usamos la expresión asintótica de
Ahora podemos hacer la integral
Tenemos
Operando igual para obtenemos para el trabajo
Integración de la definición de trabajo
Al realizar un desplazamiento diferencial el trabajo realizado por la fuerza de reacción vincular es
El desplazamiento es
Una derivada es un cociente entre dos incrementos muy pequeños. Podemos hacer entonces
Entonces el desplazamiento diferencial se puede expresar en función de las variaciones infinitesimales de y
Entonces el trabajo realizado por la fuerza de reacción vincular en un tiempo es
Utilizando otra vez la idea de que la derivada es un cociente tenemos
Por tanto el trabajo infinitesimal es
Ahora podemos calcular el trabajo en función del cambio en la coordenada radial
Obtenemos el mismo resultado que con el método anterior.
Variación de la energía cinética
La energía cinética en cada instante es
donde hemos usado la solución asintótica. Como tenemos los instantes de tiempo que corresponden a y , podemos calcular la variación de energía cinética
Podemos comprobar que la variación de la energía cinética es igual al trabajo realizado por la fuerza de reacción vincular. Se verifica así el teorema de las fuerzas vivas.





















































![{\displaystyle {\begin{array}{ll}W_{\rho =b}^{\rho =2b}&=\int \limits _{t_{b}}^{t_{2b}}P(t)\,\mathrm {d} t\\&\\&=\int \limits _{t_{b}}^{t_{2b}}{\dfrac {1}{2}}m\,\rho _{0}^{2}\,\omega ^{3}\,e^{2\omega t}\,\mathrm {d} t\\&\\&={\dfrac {1}{2}}m\,\rho _{0}^{2}\,\omega ^{3}\int \limits _{t_{b}}^{t_{2b}}\,e^{2\omega t}\,\mathrm {d} t\\&\\&={\dfrac {1}{4}}m\,\rho _{0}^{2}\,\omega ^{2}\left[e^{2\omega t}\right]_{t_{b}}^{t_{2b}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e77c2303dfecbfad6ef788d87001f2768ff55d67)













![{\displaystyle W_{\rho =b}^{\rho =2b}=\int \limits _{b}^{2b}2\,m\,\omega ^{2}\,\rho \,\mathrm {d} \rho =m\,\omega ^{2}\,\left[\rho ^{2}\right]_{b}^{2b}=3\,m\,b^{2}\,\omega ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a737f063db08a7b90c896dcff1fa4917cbf486c2)

