Aro rodando sin deslizar sobre un plano inclinado (GIC)

Enunciado

Un aro rueda por un plano inclinado con ángulo $\beta$. Se suelta desde una altura $h$ y desde el reposo. El aro rueda sin deslizar por el plano inclinado bajo la acción de la gravedad.

1. Calcula la velocidad del aro al llegar al final de la rampa con argumentos energéticos y aplicando el TCM y el TMA.
2. Si soltamos una alianza de boda, una lata de refresco vacía, una pila AAA, una canica y un ordenador portátil, ¿en que orden llegan al final de la rampa? (En el caso del ordenador se desprecia el efecto del rozamiento)

Solución

Resolución usando la conservación de energía mecánica

Energía cinética del aro

La energía cinética del aro se compone de una parte de traslación del centro de masas y una parte de rotación alrededor del centro de masas.

$T={\dfrac {1}{2}}m|{\vec {v}}|^{2}+{\dfrac {1}{2}}I_{G}|{\vec {\omega }}|^{2}.$

Aquí, $I_{G}$ es el momento de inercia del aro respecto a un eje perpendicular a él que pase por su centro de masas, localizado por simetría en su centro. La ligadura de rodadura sin deslizamiento quiere decir que el punto del aro en contacto con el plano inclinado tiene velocidad nular. Esto impone una ligadura entre la velocidad de rotación y la velocidad del centro del aro

$|{\vec {v}}|=|{\vec {\omega }}|R.$

Por ello, la energía cinética es

$T={\dfrac {1}{2}}m\,\left(1+{\dfrac {I_{G}}{mR^{2}}}\right)\,|{\vec {v}}|^{2}.$

Definimos el parámetro $\lambda$ como

$\lambda =I_{G}/mR^{2}.$

De este modo, la energía cinética se escribe

$T={\dfrac {1}{2}}m\,\left(1+\lambda \right)\,|{\vec {v}}|^{2}.$

Este parámetro nos va a permitir aplicar la solución del problema a distintos sólidos rígidos (aro, disco, esfera, etc)

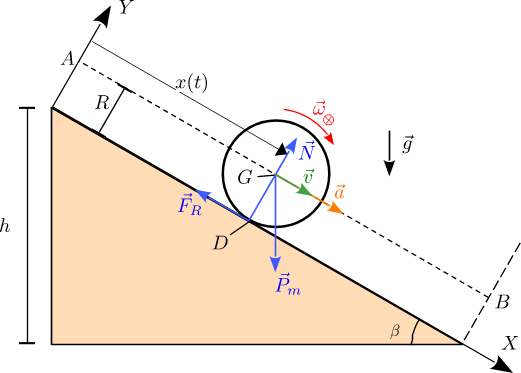
Fuerzas que actúan sobre el aro

La figura de la derecha muestra las fuerzas que actúan sobre el aro durante su movimiento. El peso es conservativo, por lo que se le puede asignar una energía potencial. La fuerza normal en $D$ actúa para que el aro no atraviese el plano inclinado. La fuerza de rozamiento se encarga de que el aro no deslice en $D$. Por eso apunta hacia arriba. Si no hubiese rozamiento, el aro deslizaría al soltarlo desde arriba y la velocidad en $D$ apuntaría hacia abajo. Para oponerse a ese deslizamiento la fuerza de rozamiento apunta hacia arriba. La potencia aportada al aro tanto por la fuerza normal como la de rozamiento es

$P_{N}={\vec {N}}\cdot {\vec {v}}_{D}=0,\qquad P_{R}={\vec {F}}_{R}\cdot {\vec {v}}_{D}=0.$

Ambas se anulan porque ${\vec {v}}_{D}={\vec {0}}$. Así pues, estas dos fuerzas no hacen trabajo y la energía mecánica se conserva.

Balance de energía mecánica

Cuando el centro del aro está en el punto $A$, el aro está en reposo. Su energía mecánica en ese instante es

$E_{m}^{A}=T_{A}+U_{A}=U_{A}.$

Cuando el centro del aro está en el punto $B$ su energía mecánica es

$E_{m}^{B}=T_{B}+U_{B}={\dfrac {1}{2}}m\,\left(1+\lambda \right)\,|{\vec {v}}_{B}|^{2}+U_{B}.$

Igualando las energía mecánicas en $A$ y en $B$ llegamos a

$|{\vec {v}}_{B}|^{2}={\dfrac {2}{m(1+\lambda )}}\,(U_{A}-U_{B}).$

La altura que desciende el aro entre $A$ y $B$ es la altura del plano inclinado, es decir

$U_{A}-U_{B}=mgh.$

Por tanto, la rapidez del centro del aro en el punto $B$ es

$|{\vec {v}}_{B}|={\dfrac {\sqrt {2gh}}{1+\lambda }}.$

Es interesante destacar que la rapidez del centro de masas en el punto final no depende ni de la masa ni del radio del aro.

Resolución usando los teoremas fundamentales

Vamos a resolver el problema aplicando el Teorema del centro de masas (TCM) y el Teorema del momento angular (TMA).

TCM

El TCM dice

$m{\vec {a}}_{G}={\vec {P}}_{m}+{\vec {N}}+{\vec {F}}_{R}.$

Proyectando los vectores en los ejes de la figura tenemos

${\begin{array}{lr}m{\vec {a}}_{G}=ma\,{\vec {\imath }},&\\{\vec {P}}_{m}=mg\,\mathrm {sen} \,\beta \,{\vec {\imath }}-mg\cos \beta \,{\vec {\jmath }},&(G)\\{\vec {N}}=N\,{\vec {\jmath }},&(N\geq 0)\qquad (D)\\{\vec {F}}_{R}=f\,{\vec {\imath }}.&(D)\end{array}}$

Hemos puesto a la derecha los puntos en los que se aplican las fuerzas. La condición $N\geq 0$ aparece porque la fuerza normal sólo puede apuntar hacia arriba, al ser el vínculo impuesto por el plano inclinado unilateral. La componente $f$ de la fuerza de rozamiento puede ser positiva, negativa o nula. Aunque en este caso esperamos que $f<0$, pues la fuerza de rozamiento debe apuntar hacia arriba.

De este modo, el TCM proporciona dos ecuaciones, una en cada dirección de los ejes

${\begin{array}{lclr}X)&\to &ma=mg\,\mathrm {sen} \,\beta +f,&(1)\\Y)&\to &0=-mg\cos \beta +N.&(2)\end{array}}$

TMA

Aplicamos el TMA en el centro de masas del aro

${\dfrac {\mathrm {d} {\vec {L}}_{G}}{\mathrm {d} t}}={\vec {M}}_{G}^{\,\mathrm {ext} }.$

El momento angular del aro en su centro de masas es

${\vec {L}}_{G}=I_{G}\,{\vec {\omega }}.$

Teniendo en cuenta la elección de los ejes $OXYZ$, la ligadura de rodar sin deslizar impone que

${\vec {\omega }}=-{\dfrac {v}{R}}\,{\vec {k}}.$

Aquí, tenemos que ${\vec {v}}_{G}=v\,{\vec {\imath }}$. Si la componente $v>0$, el vector de rotación debe apuntar hacia dentro del dibujo, es decir, en sentido contrario al eje $Z$. De ahí el signo menos en la expresión anterior. Con esto, el momento angular es

${\vec {L}}_{G}=-{\dfrac {I_{G}}{R}}\,v\,{\vec {k}}=-\lambda mRv\,{\vec {k}}.$

La derivada respecto del tiempo es

${\dfrac {\mathrm {d} {\vec {L}}_{G}}{\mathrm {d} t}}=-\lambda mR{\dfrac {\mathrm {d} v}{\mathrm {d} t}}\,{\vec {k}}=-\lambda mRa\,{\vec {k}}..$

El peso se aplica en el punto $G$, por lo que no crea momento de fuerza respecto de ese punto. La fuerza normal tampoco, pues el punto $G$ está en su recta soporte $({\overrightarrow {GD}}\times {\vec {N}}={\vec {0}})$. Así pues, sólo la fuerza de rozamiento crea momento de fuerza en $G$

${\vec {M}}_{G}^{\,\mathrm {ext} }={\overrightarrow {GD}}\times {\vec {F}}_{R}=(-R\,{\vec {\jmath }})\times (f\,{\vec {\imath }})=fR\,{\vec {k}}.$

De este modo, el TMA nos da una ecuación

$Z)\quad \to \quad -\lambda mRa=fR.\qquad (3)$

Solución de las ecuaciones

Las incógnitas son tres: $\{a,N,f\}$. La fuerza de rozamiento es desconocida pues el régimen de rozamiento es estático. La fuerza de rozamiento vale lo necesario para que el punto $D$ del aro no deslice sobre el plano inclinado. Despejando $f$ de la ecuación $(3)$ y sustituyendo en $(1)$

$a={\dfrac {g\,\mathrm {sen} \,\beta }{1+\lambda }}=a_{0}.$

El resultado es que el centro del aro se mueve con M.R.U.A. con aceleración constante $a_{0}$ definida en la expresión anterior. Teniendo en cuenta las condiciones iniciales $(x(0)=0,v(0)=0)$, tenemos, para el movimiento del centro del aro

$v=a_{0}t,\qquad x={\dfrac {1}{2}}a_{0}t^{2}.$

Las componentes de las fuerzas vinculares son

$N=mg\cos \beta ,\qquad f=-\lambda ma_{0}=-{\dfrac {\lambda }{1+\lambda }}\,mg\,\mathrm {sen} \,\beta .$

El signo negativo en $f$ indica que, efectivamente, la fuerza de rozamiento apunta hacia arriba

${\vec {F}}_{R}=-{\dfrac {\lambda }{1+\lambda }}\,mg\,\mathrm {sen} \,\beta \,{\vec {\imath }}.$

Rapidez del centro de masas en B

El instante $t_{B}$ en el que el centro del aro llega al punto $B$ se obtiene imponiendo que la coordenada $x$ del centro sea igual a la longitud del plano inclinado

$x(t_{B})={\dfrac {h}{\mathrm {sen} \,\beta }}\Longrightarrow t_{B}={\sqrt {\dfrac {2h}{a_{0}\,\mathrm {sen} \,\beta }}}={\dfrac {1}{\mathrm {sen} \,\beta }}\,{\sqrt {\dfrac {2h}{g}}}\,{\sqrt {1+\lambda }}.$

Sustituyendo en la expresión de la velocidad del centro del aro tenemos

$v_{B}=a_{0}t_{B}={\dfrac {\sqrt {2gh}}{\sqrt {1+\lambda }}}.$

Observamos de nuevo que ni el tiempo que tarda en llegar a $B$ ni la rapidez del centro en ese punto dependen de la masa o el radio del aro.

Comparación entre diferentes sólidos

El análisis que hemos hecho es válido para un aro, un disco, una esfera maciza o hueca y una cáscara cilíndrica. Podemos usar estos sólidos para modelar los objetos propuestos en el enunciado. La diferencia entre ellos se específica en el valor del parámetro $\lambda$. Podemos hacer una tabla con estos valores

Objeto	Cuerpo	$\lambda$	$v_{B}/{\sqrt {2gh}}$	$t_{B}/{\sqrt {2h/g\,\mathrm {sen} ^{2}\beta }}$
Alianza	Aro	1	${\dfrac {1}{\sqrt {2}}}=0.71$	${\sqrt {2}}=1.41$
Lata	Cáscara cilíndrica con tapas	$\approx 0.9$	$0.73$	$1.38$
Pila	Cilindro	${\dfrac {1}{2}}=0.5$	${\sqrt {2/3}}=0.82$	${\sqrt {3/2}}=1.22$
Canica	Esfera maciza	${\dfrac {2}{5}}=0.4$	${\sqrt {7/5}}=0.85$	${\sqrt {5/7}}=1.18$
Ordenador (sin roz)	Partícula puntual	$0$	$1$	$1$

El valor de $\lambda$ para la lata se explica porque la modelamos con una cáscara cilíndrica (que tendría un valor $\lambda =1$) con dos discos añadidos para tener en cuenta las tapas. Eso hace que $\lambda$ sea un poquito menor que 1. Para el ordenador, se modela como una partícula puntual, que no puede rotar. Por tanto, el momento de inercia sería nulo, lo que corresponde a $\lambda =0$.

Vemos que en ausencia de rozamiento el que llega primero es el ordenador. Eso se debe a que, al no tener rotación, la energía potencial disponible en $A$ se transforma íntegramente en energía cinética de traslación. Para los sólidos en los que si hay rotación, parte de la energía potencial se convierte en energía cinética de rotación, por lo que queda menos energía para la parte de traslación. Así, el objeto que llega antes es el que tiene un momento de inercia menor, es decir, un valor de $\lambda$ mas pequeño. Esto ilustra la idea de que el momento de inercia es una medida de la inercia del sólido frente a rotaciones.