Placa cuadrada empujada contra una pared (Ene. 2020 G.I.C.)

Enunciado

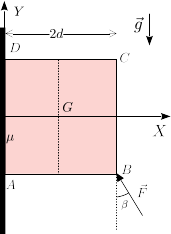
Una placa cuadrada de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} y lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2d} se apoya en una pared vertical rugosa con coeficiente de rozamiento estático Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu=1} . Una fuerza Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}} empuja el bloque contra la pared. El módulo de la fuerza es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_0} y forma un ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \beta} con el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_1} . La gravedad actúa como se indica en la figura. El ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \beta} verifica

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\,\beta = \dfrac{3}{5}, \qquad \cos\beta = \dfrac{4}{5}. }

1. Dibuja el diagrama de cuerpo libre de la placa.
2. Calcula el valor de las fuerzas que actúan sobre la placa en condiciones de equilibrio estático.
3. ¿Que condiciones debe cumplir $F_{0}$ para que la placa no deslice?
4. ¿Que condiciones debe cumplir Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_0} para que la placa no vuelque respecto a la pared?
5. ¿Que condiciones debe cumplir Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_0} para que la placa ni deslice ni vuelque respecto a la pared?

Solución

Diagrama de fuerzas

La figura de la derecha muestra las fuerzas que actúan sobre la placa: la fuerza aplicada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}} , el peso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{P}_g} , la fuerza vincular normal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}} y la fuerza de rozamiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{E}_R} . Expresamos estas fuerzas en el sistema de ejes de la figura

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lr} \vec{F} = -F_0\,\mathrm{sen}\,\beta\,\vec{\imath} + F_0\cos\beta\,\vec{\jmath} = -\dfrac{3}{5}\,\vec{\imath} + \dfrac{4}{5}\,\vec{\jmath} & (B)\\ \vec{P}_g = -mg\,\vec{\jmath} & (G)\\ \vec{E} = E\,\vec{\imath} & (E)\\ \vec{E}_R = E_R\,\vec{\jmath} & (E)\\ \end{array} }

Indicamos a la derecha el punto donde se aplican estas fuerzas. Todas ellas son vectores deslizantes, por lo que se pueden deslizar sobre sus respectivas rectas soporte.

Situación de equilibrio estático

Para que un sólido rígido esté en equilibrio estático deben cumplirse dos condiciones

$\sum \limits _{i}{\vec {F}}_{i}={\vec {0}},\qquad \sum \limits _{i}{\vec {M}}_{Pi}={\vec {0}}.$

Es decir, que la suma vectorial de fuerzas que actúan sobre el sólido se anule y que el momento de fuerzas neto respecto a un punto cualquiera que actúen sobre el sólido también se anule.

La condición sobre la suma de fuerzas proporciona dos ecuaciones

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}+\vec{P}_g+\vec{E}+\vec{E}_R = \vec{0} \to \left\{ \begin{array}{llr} X): & -\dfrac{3}{5}F_0+ E = 0 & (1)\\ &&\\ Y): & \dfrac{4}{5}F_0 + E_R - mg = 0 & (2) \end{array} \right. }

Elegimos el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle H} de la figura para calcular los momentos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{M}_H = \overrightarrow{HG}\times\vec{P}_g + \overrightarrow{HB}\times\vec{F} + \overrightarrow{HE}\times\vec{E} = \vec{0}. }

Los momentos son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \overrightarrow{HG}\times\vec{P}_g = (d\,\vec{\imath})\times(-mg\,\vec{\jmath}) = -mgd\,\vec{k},\\ \\ \overrightarrow{HB}\times\vec{F} =(2d\,\vec{\imath} - d\,\vec{\jmath})\times\left(-\dfrac{3}{5}F_0\,\vec{\imath} + \dfrac{4}{5}F_0\,\vec{\jmath}\right) = F_0d\,\vec{k},\\ \overrightarrow{HE}\times\vec{P}_g = (\delta\,\vec{\jmath})\times(E\,\vec{\imath}) = -E\delta\,\vec{k}. \end{array} }

Obtenemos la ecuación

$F_{0}d-mgd-E\delta =0\qquad (3)$

Tenemos tres incógnitas: $\{E,E_{R},\delta \}$ para tres ecuaciones. Resolviendo el sistema obtenemos

${\begin{array}{l}{\vec {E}}={\dfrac {3}{5}}F_{0}\,{\vec {\imath }},\\\\{\vec {E}}_{R}=\left(mg-{\dfrac {4}{5}}F_{0}\right)\,{\vec {\imath }},\\\\\delta ={\dfrac {5}{3}}\,\left(1-{\dfrac {mg}{F_{0}}}\right)\,d.\end{array}}$

Análisis del deslizamiento

Para que no deslice debe cumplirse

$|{\vec {E}}_{R}|\leq \mu |{\vec {E}}|\Longrightarrow \left|mg-{\dfrac {4}{5}}F_{0}\right|\leq {\dfrac {3}{5}}F_{0}\Longrightarrow |5mg-4F_{0}|\leq 3F_{0}.$

Hemos usado que $\mu =1$. Tenemos que considerar dos posibles situaciones:

$5mg>4F_{0}$

Entonces se tiene $|5mg-4F_{0}|=5mg-4F_{0}$ y la condición queda

$5mg-4F_{0}\leq 3F_{0}\Longrightarrow F_{0}\geq 5mg/7.$

En este caso la fuerza de rozamiento apunta hacia arriba e impide que la placa deslice hacia abajo.

$5mg<4F_{0}$

Entonces se tiene Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle |5mg-4F_0| = 4F_0-5mg} y la condición queda

$4F_{0}-5mg\leq 3F_{0}\Longrightarrow F_{0}\leq 5mg.$

En este caso la fuerza de rozamiento apunta hacia abajo e impide que la placa deslice hacia arriba.

Resumiendo las dos condiciones, para que no haya deslizamiento debe ocurrir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_0\in \left[\dfrac{5}{7}mg, 5mg\right] = [0.714mg, 5mg] }

Análisis del vuelco

Para que la placa no vuelque debe ocurrir que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -d\leq\delta\leq d. }

La condición de la izquierda es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{5}{3}\,\left(1-\dfrac{mg}{F_0}\right)\,d\geq -d \to 5-\dfrac{5mg}{F_0} \geq -3 \to 8 \geq \dfrac{5mg}{F_0} \to F_0\geq \dfrac{5}{8}mg. }

La condición de la derecha es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{5}{3}\,\left(1-\dfrac{mg}{F_0}\right)\,d\leq d \to 5-\dfrac{5mg}{F_0} \leq 3 \to 2 \leq \dfrac{5mg}{F_0} \to F_0\leq \dfrac{5}{2}mg. }

Es decir, para que no vuelque debe ocurrir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_0\in \left[\dfrac{5}{8}mg, \dfrac{5}{2}mg\right] = [0.625mg, 2.5mg] }

Condición para que ni vuelque ni deslice

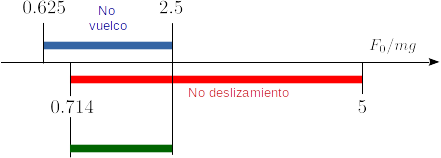
Para que ocurra esto deben cumplirse a la vez las condiciones de no deslizamiento y no vuelco. La figura de la derecha muestra los intervalos de valores de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_0/mg} para los que hay equilibrio frente a vuelco. Para que se cumplan las dos cosas a la vez debe ocurrir

$F_{0}\in [0.714mg,2.5mg]$