Sonda espacial

Enunciado

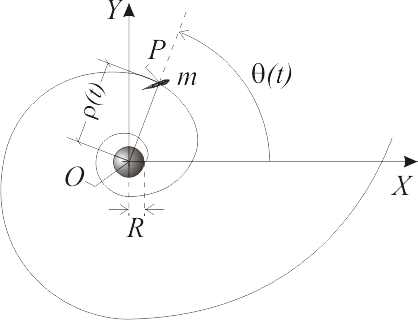
Una sonda espacial, considerada como un punto material Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P\,} de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\,} , se mueve en el plano OXY (descrito mediante las coordenadas polares Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta\,} de la figura) cuyo origen Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} coincide con el centro de un planeta de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R\,} . Éste ejerce sobre la sonda una fuerza de atracción gravitatoria conservativa, cuya energía potencial asociada viene dada por la expresión:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U(\rho)=-\frac{\gamma m}{\rho} \;\;\;\;\;\;\;\;\;\;\;\; \mathrm{(}\gamma\,\,\mathrm{es}\,\,\mathrm{una}\,\,\mathrm{constante}\,\, \mathrm{conocida)} }

Mediante la acción de sus motores, la sonda es puesta en órbita desde la superficie del planeta siguiendo la espiral logarítmica de ecuaciones horarias:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho(t)=R\, e^{\lambda\omega t}\,\, ; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\theta(t)=\omega t\;\;\;\;\;\;\;\;\;\;\;\; \mathrm{(}\lambda\,\,\mathrm{y}\,\,\omega\,\,\mathrm{son}\,\,\mathrm{constantes}\,\,\mathrm{conocidas)} }

Despreciando las posibles fuerzas de fricción sobre la sonda, así como las pérdidas de masa asociadas al gasto de combustible, se pide:

1. Deducir razonadamente si el movimiento de la sonda es o no es un movimiento central con centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} .
2. Comprobar que la energía cinética de la sonda responde a la expresión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K=C\rho^2\,} , determinando el valor de la constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C\,} en función de las constantes conocidas del problema.
3. Aplicando el teorema de la energía mecánica, determinar el trabajo (no conservativo) realizado por los motores sobre la sonda durante el intervalo de tiempo que tarda ésta en duplicar su distancia inicial al centro del planeta.

¿Es un movimiento central con centro en el punto O?

Si el movimiento de la sonda tuviese lugar bajo una fuerza neta central con centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} , entonces su momento cinético (y su velocidad areolar) respecto a dicho punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} serían constantes a lo largo del tiempo. Comprobemos si ocurre o no tal cosa.

Sustituyendo las expresiones generales (en coordenadas polares) de los vectores de posición y velocidad de una partícula

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \vec{r} & = & \rho\,\vec{u}_{\rho} \\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta}\end{array}}

en la definición del momento cinético de la partícula respecto al origen de coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} , se obtiene:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{L}_O=2m\vec{V}_A=\vec{r}\times m\vec{v}=\rho\,\vec{u}_{\rho}\times m(\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta})=m\rho^2\dot{\theta}\,\vec{k}}

Conocemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho\,} en función del tiempo (ecuación horaria radial), y determinamos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}=\omega\,} derivando respecto al tiempo la ecuación horaria acimutal. Y sustituyendo en la expresión del momento cinético, se obtiene:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{L}_O=2m\vec{V}_A=m\rho^2\dot{\theta}\,\vec{k}=m\omega R^2 e^{2\lambda\omega t}\,\vec{k}}

Observamos que el momento cinético (y la velocidad areolar) respecto a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} varía con el tiempo. Concluimos, por tanto, que el movimiento de la sonda NO es central con centro en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} .

Energía cinética

La energía cinética Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K\,} de la sonda se puede expresar en función de las coordenadas polares y de sus primeras derivadas respecto al tiempo:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K=\frac{1}{2}\,mv^2=\frac{1}{2}\,m(\vec{v}\cdot\vec{v})=\frac{1}{2}\, m(\dot{\rho}^2+\rho^2\dot{\theta}^2)}

Calculando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\rho}\,} por derivación de la ecuación horaria radial:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\rho}=\lambda\,\omega R e^{\lambda\,\omega\, t}=\lambda\,\omega\rho}

y sustituyendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\rho}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}\,} en la expresión de la energía cinética, queda:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K=\frac{1}{2}\, m(\lambda^2\omega^2\rho^2+\omega^2\rho^2)=\frac{1}{2}\, m(\lambda^2+1)\,\omega^2\rho^2}

Por tanto, la energía cinética de la sonda resulta ser proporcional al cuadrado de su distancia al centro del planeta:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K=C\rho^2\, }

donde se ha denominado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C\,} a la siguiente constante:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C=\displaystyle\frac{1}{2}\, m(\lambda^2+1)\,\omega^2 }

Trabajo (no conservativo)

Dado que el enunciado del problema nos permite despreciar las fuerzas de fricción, las únicas fuerzas que realizan trabajo sobre la sonda durante su movimiento son la gravitatoria ejercida por el planeta (conservativa) y la fuerza motora (no conservativa). Al estar trabajando una fuerza no conservativa, sabemos que la energía mecánica de la sonda (suma de su energía cinética y su energía potencial gravitatoria) no se va a conservar constante en el tiempo. La variación de dicha energía mecánica será precisamente igual al trabajo realizado por la fuerza motora no conservativa.

Por tanto, para determinar el trabajo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W^{\mathrm{nc}}\,} realizado por los motores durante el intervalo de tiempo en el que la sonda duplica su distancia inicial al centro del planeta (es decir, pasa de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho=R\,} a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho=2R\,} ), basta calcular la variación de su energía mecánica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta E\,} durante dicho intervalo:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W^{\mathrm{nc}} = \Delta E=\Delta K+\Delta U=[K(2R)-K(R)]+[U(2R)-U(R)]= C(4R^2-R^2)-\gamma m\left(\displaystyle\frac{1}{2R}-\frac{1}{R}\right)=3\, CR^2+\displaystyle\frac{\gamma m}{2R} }

siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C\,} la constante definida al final del apartado anterior.