Disco articulado con una varilla (G.I.A.)

Enunciado

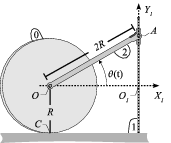
El mecanismo de la figura está formado por un disco (sólido "0"), de radio $R$; y por una varilla $OA$ (sólido "2"), de longitud $2R$, articulada en su extremo $O$ al centro del disco. El disco rueda sin deslizar sobre la recta fija (sólido "1") de ecuación $y_{1}=-R$, mientras que el extremo $A$ de la varilla está obligado a deslizar sobre el eje $O_{1}Y_{1}$. Sabiendo que el mecanismo se mueve conforme a la ley horaria $\theta (t)=\omega t$ (donde $\omega$ es una constante conocida), se pide:

1. Los vectores de posición, ${\overrightarrow {O_{1}A}}={\vec {r}}_{21}^{A}(t)$; velocidad, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^A(t)} ; y aceleración Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}_{21}^A(t)} , del movimiento absoluto del extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} de la varilla. ¿Qué tipo de movimiento describe dicho punto?
2. Reducciones cinemáticas (vectores velocidad angular y velocidad de un punto) de los movimientos {21}, {01} y {20}.
3. Determinación gráfica y analítica de la posición del C.I.R. del movimiento {21}.

Solución

Cálculo del vector de posición, velocidad y aceleración del punto A en el movimiento {21}

El extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} de la varilla está situado siempre sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1Y_1} . Su posición puede determinarse en la escuadra "1" como

${\vec {r}}_{21}^{A}={\overrightarrow {O_{1}A}}=2R\,\,\mathrm {sen} \,\theta \,{\vec {\jmath }}_{1}=2R\,\,\mathrm {sen} \,(\omega t)\,{\vec {\jmath }}_{1}$

Como esta expresión es válida en todo instante y está expresada en la base del sólido "1", podemos derivarla para calcular la velocidad y la aceleración pedidas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{v}_{21}^A = \left.\dfrac{\mathrm{d}\vec{r}_{21}^A}{\mathrm{d}t}\right|_1=2R\omega\,\cos(\omega t)\,\vec{\jmath}_1\\ \\ \vec{a}_{21}^A = \left.\dfrac{\mathrm{d}\vec{v}_{21}^A}{\mathrm{d}t}\right|_1=-2R\omega^2\,\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}_1 \end{array} }

Para determinar el tipo de movimiento que realiza el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} , observemos que se cumple

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}_{21}^A=\ddot{\vec{r}}_{21}^A=-\omega^2\vec{r}_{21}^A\Rightarrow \ddot{y}_{21}^A=-\omega^2{y}_{21}^A }

Es decir, es un movimiento armónico simple a lo largo del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1Y_1} , centrado en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1} , de frecuencia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega} y amplitud $2R$.

Reducciones cinemáticas de los movimientos

Movimiento {21}

Hemos calculado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^A} . Para determinar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21}} necesitamos la velocidad en otro punto. Para ello vamos a expresar la posición del otro extremo de la varilla en la base de la escuadra Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1X_1Y_1} . El punto $O$ se mueve siempre a lo largo del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1X_1} . Por trigonometría tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{O_1O} = -2R\,\cos\theta\,\vec{\imath}_1=-2R\,\cos(\omega t)\,\vec{\imath}_1 }

De nuevo podemos derivar esta expresión para calcular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^O}

${\vec {v}}_{21}^{O}=\left.{\dfrac {\mathrm {d} {\vec {v}}_{21}^{O}}{\mathrm {d} t}}\right|_{1}=2R\omega \,\,\mathrm {sen} \,(\omega t)\,{\vec {\imath }}_{1}$

Teniendo en cuenta que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21}=\omega_{21}\,\vec{k}} , la ecuación del campo de velocidades nos permite plantear la ecuación

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{c} \vec{v}_{21}^A=\vec{v}_{21}^O+\vec{\omega}_{21}\times\overrightarrow{OA}= \vec{v}_{21}^O+ \left| \begin{array}{ccc} \vec{\imath}_1&\vec{\jmath}_1&\vec{k}_1\\0&0&\omega_{21}\\2R\cos(\omega t)&2R\,\mathrm{sen}\,(\omega t)&0 \end{array} \right|\Rightarrow\\ \\ \left( \begin{array}{c} 0\\2R\omega\cos(\omega t) \end{array} \right)= \left( \begin{array}{c} (w-\omega_{21})2R\cos(\omega t)\\2R\omega_{21}\cos(\omega t) \end{array} \right) \end{array} }

Por tanto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{21}=\omega} y la reducción en el punto $O$ es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21}=\omega\,\vec{k}\qquad\qquad\vec{v}_{21}^O=2R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1 }

Movimiento {01}

El disco rueda sin deslizar sobre la línea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y_1=-R} . Por tanto el punto de contacto es el CIR y su velocidad en este movimiento es nula, ${\vec {v}}_{01}^{C}={\vec {0}}$. Por otro lado, aún no podemos determinar la velocidad angular de este movimiento. Por tanto lo que sabemos por ahora es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{01}=\omega_{01}\,\vec{k}\qquad\qquad\vec{v}_{01}^C=\vec{0} }

Movimiento {20}

El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O} pertenece tanto al sólido "2" como al "0". Por tanto es un punto fijo en este movimiento. La reducción en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O} es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20}=\omega_{20}\,\vec{k}\qquad\qquad\vec{v}_{20}^O=\vec{0} }

Composición {21} = {20} + {01}

La velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^O} puede escribirse

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^O=\vec{v}_{20}^O+\vec{v}_{01}^O\Rightarrow \vec{v}_{01}^O=\vec{v}_{21}^O-\vec{v}_{20}^O }

donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^O} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{20}^O} son conocidas. Ahora podemos calcular ${\vec {v}}_{01}^{O}$

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{01}^O=\vec{v}_{01}^C+\vec{\omega}_{01}\times\overrightarrow{CO}=(\omega_{01}\,\vec{k})\times(R\,\vec{\jmath}_1)=-R\omega_{01}\,\vec{\imath}_1 }

Sustituyendo tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -R\omega_{01}\,\vec{\imath}_1=2R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1 \Rightarrow \vec{\omega}_{01}=-2\omega\,\mathrm{sen}\,(\omega t)\,\vec{k} }

Para obtener Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20}} recurrimos a la composición de velocidades angulares

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\Rightarrow\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}=\omega(1+2\,\mathrm{sen}\,(\omega t))\,\vec{k} }

Por tanto, las reducciones pedidas son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lclcl} \{21\}&\longrightarrow&\vec{\omega}_{21}=\omega\,\vec{k}&\qquad\qquad&\vec{v}_{21}^O=2R\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1\\ &&&&\\ \{20\}&\longrightarrow&\vec{\omega}_{20}=\omega(1+2\,\mathrm{sen}\,(\omega t))\,\vec{k}&\qquad\qquad&\vec{v}_{20}^O=\vec{0}\\ &&&&\\ \{01\}&\longrightarrow&\vec{\omega}_{01}=-2\omega\,\mathrm{sen}\,(\omega t)\,\vec{k}&\qquad\qquad&\vec{v}_{01}^C=\vec{0} \end{array} }

Determinación del CIR del movimiento {21}

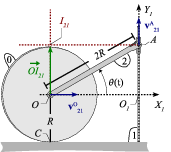
Gráfica

Tenemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^O} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^A} . Si trazamos en cada punto la recta perpendicular a sus velocidades respectivas el punto de corte nos da Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I_{21}} , como se indica en el dibujo

Analítica

Partiendo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_{21}^O} , la posición de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I_{21}} es

${\overrightarrow {OI}}_{21}={\dfrac {{\vec {\omega }}_{21}\times {\vec {v}}_{21}^{O}}{|{\vec {\omega }}_{21}|^{2}}}=2R\,\mathrm {sen} \,(\omega t)\,{\vec {\jmath }}_{1}$

Podemos comprobar que ambos métodos dan el mismo resultado.