Barra rotando con muelle horizontal (MRGIC)

Enunciado

Barra rotando con muelle horizontal

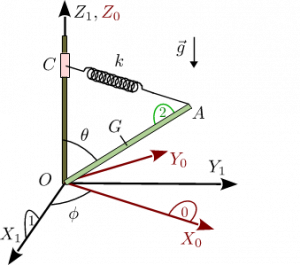
El mecanismo de la figura está formado por una varilla delgada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OA} (sólido "2"), de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} y longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L} , y un resorte ideal de constante recuperadora Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle k} y longitud natural nula. El extremo $O$ de la varilla está unido mediante una rótula ideal al origen de un sistema de referencia fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1Y_1Z_1} (sólido "1"). El otro extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} de la varilla está conectado mediante el resorte a un pasador Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} de masa despreciable que puede deslizar libremente y sin rozamiento por el eje vertical Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OZ_1} . En todo momento la orientación del eje del resorte es perpendicular a $OZ_{1}$. Se aplica un par motor externo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\tau}=\tau\,\vec{k}_0} al sólido "2" que le obliga a rotar con velocidad angular ${\dot {\phi }}=\omega _{0}$ constante.

1. Obtén el valor de una integral primera del movimiento.
2. Obtén el valor del par motor necesario para que se verifique el vínculo.

Solución

Integral primera en el movimiento descrito

Reutilizando los cálculos que hicimos en barra articulada rotando en el espacio, la reducción cinemática del movimiento absoluto de la barra es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21} = \dot{\theta}\,\vec{\jmath}_0 + \dot{\phi}\,\vec{k}_0, \qquad \vec{v}^{\,O}_{21} = \vec{0}. }

Su energía cinética es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T = \dfrac{1}{2}I\,(\dot{\phi}^2\,\mathrm{sen}^2\theta + \dot{\theta}^2). \qquad (I = mL^2/3) }

El problema libre tiene dos grados de libertad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\phi, \theta \} } . Sin embargo, en este caso la rotación asociada a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi } está fijada por el vínculo cinemático

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi} = \omega_0. }

Es decir, el sistema tiene sólo un grado de libertad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\theta\} } .

Aplicando el vínculo, la energía cinética es

$T={\dfrac {1}{2}}I\,(\omega _{0}^{2}\,\mathrm {sen} ^{2}\theta +{\dot {\theta }}^{2}).$

En este caso hay dos interacciones conservativas actuando sobre el muelle: la gravedad y el muelle. Podemos asociar una energía potencial a cada una de ellas. Tomando como referencia de altura para la energía potencial gravitatoria la del plano fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1Y_1 } tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} U_g = - m\vec{g}\cdot\overrightarrow{OG} = \dfrac{1}{2}mgL\cos\theta, \\ U_m = \dfrac{1}{2}k |\overrightarrow{CA}|^2 = \dfrac{1}{2}kL^2\,\mathrm{sen}^2\theta. \end{array} }

Hemos usado que el muelle tiene longitud natural nula.

La función de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L = T - (U_g + U_m) = \dfrac{1}{2}I\,(\omega_0^2\,\mathrm{sen}^2\theta + \dot{\theta}^2) - \dfrac{1}{2}mgL\cos\theta - \dfrac{1}{2}kL^2\,\mathrm{sen}^2\theta. }

La primera opción para buscar integrales primeras es la energía mecánica. Sin embargo, en este caso la energía mecánica no se conserva. El par que hace rotar la barra alrededor del eje transmite una potencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P = \vec{\tau}\cdot\vec{\omega}_{21} = \tau\omega_0 \neq 0. }

Se trata de un vínculo reónomo. Con estos vínculos no se conserva la energía mecánica debido al trabajo que hace un agente externo.

La siguiente opción es buscar alguna coordenada cíclica en la funcion de Lagrange. Pero la única coordenada sí apaerece en la lagrangiana. Entonces no hay momentos generalizados que se conserven.

Queda la opción de comprobar si la función de Hamilton se conserva. Como el sistema es reónomo, la función de Hamilton no es la energía mecánica. En este problema, sería

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle H = p_{\theta}\dot{\theta} - L(\theta, \dot{\theta}) }

La derivada temporal total es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}H}{\mathrm{d}t} = \dfrac{\mathrm{d}p_{\theta}}{\mathrm{d}t}\dot{\theta} + p_{\theta}\ddot{\theta} - \dfrac{\partial L }{\partial\theta }\dot{\theta} - \dfrac{\partial L}{\partial\dot{\theta} }\ddot{\theta} - \dfrac{\partial L}{\partial t }. }

Los términos segundo y cuarto se anulan porque, por definición,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_{\theta} = \dfrac{\partial L}{\partial \dot{\theta}}. }

El primer y tercer término se anulan porque la ecuación de Lagrange para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta } es

${\dfrac {\mathrm {d} p_{\theta }}{\mathrm {d} t}}={\dfrac {\partial L}{\partial \theta }}.$

Así pues, tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}H}{\mathrm{d}t} = -\dfrac{\partial L}{\partial t } = 0. }

En este problema la función de Hamilton es una constante, es decir, una integral primera del movimiento. Su valor es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle H = p_{\theta}\dot{\theta} - L(\theta, \dot{\theta}) = \dfrac{1}{2}mL^2\,(\dot{\theta}^2 - \omega_0^2) + \dfrac{1}{2}mgL\cos\theta + \dfrac{1}{2}kL^2\mathrm{sen}^2\theta. }

Valor del par motor

Nos pregunta el problema cuál es el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \tau_0} para que la barra tenga la rotación indicada en el enunciado. Para averiguarlo podemos aplicar el Principio de liberación. Así pues, ahora consideramos que las dos coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\phi, \theta \} } son libres. Ahora la energía cinética viene dada por la expresión completa, y es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T = \dfrac{1}{2}I\,(\dot{\phi}^2\,\mathrm{sen}^2\theta + \dot{\theta}^2). \qquad (I = mL^2/3) }

La función de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L = T - (U_g + U_m) = \dfrac{1}{2}I\,(\dot{\phi}^2\,\mathrm{sen}^2\theta + \dot{\theta}^2) - \dfrac{1}{2}mgL\cos\theta - \dfrac{1}{2}kL^2\,\mathrm{sen}^2\theta. }

Al liberar el vínculo para $\phi$, añadimos el par Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\tau}=\tau_0\vec{k}_0 } . Ahora tenemos dos ecuaciones de Lagrange

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \dfrac{\mathrm{d} }{\mathrm{d} t }\left(\dfrac{\partial L }{\partial \dot{\theta}}\right) - \dfrac{\partial L}{\partial \theta} = Q^{\,NC}_{\theta}, \\ \dfrac{\mathrm{d} }{\mathrm{d} t }\left(\dfrac{\partial L }{\partial \dot{\phi}}\right) - \dfrac{\partial L}{\partial \phi} = Q^{\,NC}_{\phi}. \end{array} }

Las fuerzas generalizadas vienen del par que hemos añadido

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} Q^{\,NC}_{\theta} = \vec{\tau}\cdot\dfrac{\partial \vec{\omega}_{21} }{\partial \dot{\theta}} = 0,\\ Q^{\,NC}_{\phi} = \vec{\tau}\cdot\dfrac{\partial \vec{\omega}_{21} }{\partial \dot{\phi}} = \tau_0, \end{array} }

Las ecuaciones de Lagrange son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} I\ddot{\theta} - I\dot{\phi}^2\mathrm{sen}\,\theta\cos\theta - \dfrac{1}{2}mgL\,\mathrm{sen}\,\theta + kL^2\mathrm{sen}\,\theta\cos\theta = 0, \\ I\,(\ddot{\phi}\,\mathrm{sen}^2\theta + \dot{\phi}\dot{\theta}\,\mathrm{sen}\,(2\theta)) = \tau_0. \end{array} }

Al aplicar el vínculo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi} = \omega_0 } , la primera de estas ecuaciones proporciona la ecuación de movimiento para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta(t) }

$I{\ddot {\theta }}={\dfrac {1}{2}}I\omega _{0}^{2}\,\mathrm {sen} \,(2\theta )+{\dfrac {1}{2}}mgL\,\mathrm {sen} \,\theta -{\dfrac {1}{2}}kL^{2}\mathrm {sen} \,(2\theta ).$

Una vez resuelta esta ecuación, con las condiciones iniciales que sean, obtendríamos la ley horaria Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta(t) } . Esta ley horaria la usaríamos en la segunda ecuación para obtener el valor del par motor necesario para que la barra rote como especifica el enunciado

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \tau_0 = I\omega_0\,\dot{\theta}\mathrm{sen}\,(2\theta). }