Diferencia entre revisiones de «Sistema de cuatro condensadores (GIOI)»
(Página creada con «==Enunciado== right {{nivel|3}} El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: <math>C_1=30\,\mathrm{nF}</math>, <math>C_2=60\,\mathrm{nF}</math>, <math>C_3=120\,\mathrm{nF}</math> y <math>C_4=40\,\mathrm{nF}</math>. La diferencia de potencial entre A y B es de <math>12\,\mathrm{V}</math>. # ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E? # Calcule la ca…») |
Sin resumen de edición |
||
| Línea 8: | Línea 8: | ||
# Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada? | # Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada? | ||
==Interruptor abierto== | ==Interruptor abierto== | ||
Con el interruptor abierto el sistema consiste en una asociación en paralelo de dos asociaciones en serie. | |||
===Cargas y potenciales=== | ===Cargas y potenciales=== | ||
Los condensadores 1 y 2, de la rama superior, están en serie, por ello, la carga en ambos es la misma | |||
<center><math>Q_1=Q_2\,</math></center> | |||
mientras que las d.d.p. se suman | |||
<center><math>V_A-V_B = (V_A - V_D)+(V_D - V_B) = \frac{Q_1}{C_1}+\frac{Q_2}{C_2}=Q_1 \left(\frac{1}{C_1}+\frac{1}{C_2}\right)</math></center> | |||
poniendo números obtenemos para la inversa de la capacidad equivalente | |||
<center><math>\frac{1}{C_1}+\frac{1}{C_2}=\frac{1}{30\,\mathrm{nF}}+\frac{1}{60\,\mathrm{nF}}=\frac{1}{20\,\mathrm{nF}}</math></center> | |||
lo que nos da la carga de ambos condensadores | |||
<center><math>Q_1=Q_2= C_{12}(V_A-V_B)=20\,\mathrm{nF}\cdot 12\,\mathrm{V}=240\,\mathrm{nC}</math></center> | |||
y la diferencia de potencial en cada condensador | |||
<center><math>\Delta V_1 = \frac{Q_1}{C_1}=\frac{240}{30}\,\mathrm,{V}=8\,\mathrm{V}\qquad\qquad \Delta V_2 = \frac{Q_2}{C_2}=\frac{240}{60}\,\mathrm,{V}=4\,\mathrm{V}</math></center> | |||
De la misma manera, operamos para la rama inferior. De nuevo, las cargas son iguales | |||
<center><math>Q_3=Q_4\,</math></center> | |||
y las d.d.p. se suman | |||
<center><math>V_A-V_B = (V_A - V_E)+(V_E - V_B) = \frac{Q_3}{C_3}+\frac{Q_4}{C_4}=Q_3 \left(\frac{1}{C_3}+\frac{1}{C_4}\right)</math></center> | |||
siendo ahora la inversa de la capacidad equivalente | |||
<center><math>\frac{1}{C_3}+\frac{1}{C_4}=\frac{1}{120\,\mathrm{nF}}+\frac{1}{40\,\mathrm{nF}}=\frac{1}{30\,\mathrm{nF}}</math></center> | |||
lo que nos da la carga de ambos condensadores | |||
<center><math>Q_3=Q_4= C_{34}(V_A-V_B)=30\,\mathrm{nF}\cdot 12\,\mathrm{V}=360\,\mathrm{nC}</math></center> | |||
y la diferencia de potencial en cada condensador | |||
<center><math>\Delta V_3 = \frac{Q_3}{C_3}=\frac{360}{120}\,\mathrm,{V}=3\,\mathrm{V}\qquad\qquad \Delta V_4 = \frac{Q_4}{C_4}=\frac{360}{40}\,\mathrm,{V}=9\,\mathrm{V}</math></center> | |||
===Lectura del voltímetro=== | |||
Una vez que tenemos las diferencias de potencial en cada condensador, calculamos la d.d.p. en la rama central | |||
<center><math>V_D - V_E = (V_D - V_B) - (V_E - V_B) = 4\,\mathrm{V}-9\,\mathrm{V}=-5\,\mathrm{V}</math></center> | |||
===Energía almacenada=== | ===Energía almacenada=== | ||
=== | Podemos calcular la energía almacenada sumando la de los cuatro condensadores | ||
<center><math>U_\mathrm{e}=\frac{1}{2}Q_1\,\Delta V_1+\frac{1}{2}Q_2\,\Delta V_2+\frac{1}{2}Q_3\,\Delta V_3+\frac{1}{2}Q_4\,\Delta V_4</math></center> | |||
lo que nos da | |||
<center><math>U_\mathrm{e}=\frac{1}{2}240\cdot 8+\frac{1}{2}240\cdot 4+\frac{1}{2}360\cdot 3+\frac{1}{2}360\cdot 9 = 3600\,\mathrm{nJ}=3.6\,\mu\mathrm{J}</math></center> | |||
También podemos llegar a este resultado considerando el sistema como un solo condensador de capacidad equivalente la suma de la de las dos ramas | |||
<center><math>C_\mathrm{eq}=20\,\mathrm{nF}+30\,\mathrm{nF}=50\,\mathrm{nF}</math></center> | |||
lo que da | |||
<center><math>U_e = \frac{1}{2}50\cdot(12)^2=3.6\,\mu\mathrm{J}</math></center> | |||
==Interruptor cerrado== | ==Interruptor cerrado== | ||
===Cargas y potenciales=== | ===Cargas y potenciales=== | ||
===Energía almacenada=== | ===Energía almacenada=== | ||
===Circuito equivalente=== | ===Circuito equivalente=== | ||
Revisión del 18:27 10 abr 2025
Enunciado
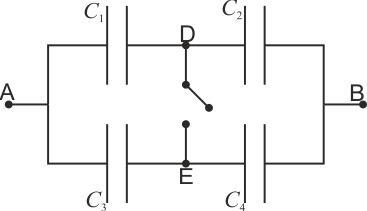
![]() El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: , , y . La diferencia de potencial entre A y B es de .
El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: , , y . La diferencia de potencial entre A y B es de .
- ¿Qué diferencia de potencial mide un voltímetro situado entre los puntos D y E?
- Calcule la carga de cada condensador y la diferencia de potencial entre las placas de cada uno, así como la energía almacenada en el sistema.
- Suponga que, sin desconectar la fuente, se cierra el interruptor entre los puntos D y E. Tras la conexión, ¿cuánto valen las cargas, los voltajes y la energía almacenada?
Interruptor abierto
Con el interruptor abierto el sistema consiste en una asociación en paralelo de dos asociaciones en serie.
Cargas y potenciales
Los condensadores 1 y 2, de la rama superior, están en serie, por ello, la carga en ambos es la misma
mientras que las d.d.p. se suman
poniendo números obtenemos para la inversa de la capacidad equivalente
lo que nos da la carga de ambos condensadores
y la diferencia de potencial en cada condensador
De la misma manera, operamos para la rama inferior. De nuevo, las cargas son iguales
y las d.d.p. se suman
siendo ahora la inversa de la capacidad equivalente
lo que nos da la carga de ambos condensadores
y la diferencia de potencial en cada condensador
Lectura del voltímetro
Una vez que tenemos las diferencias de potencial en cada condensador, calculamos la d.d.p. en la rama central
Energía almacenada
Podemos calcular la energía almacenada sumando la de los cuatro condensadores
lo que nos da
También podemos llegar a este resultado considerando el sistema como un solo condensador de capacidad equivalente la suma de la de las dos ramas
lo que da



















