Diferencia entre revisiones de «Barras articuladas con articulación en esquina, Junio 2024 (G.I.C.)»
(Página creada con «= Enunciado = 350px|derecha La barra "2", de longitud <math>\sqrt{2}L_0</math>, está articulada en el punto fijo <math>B</math>, perteneciente al sólido "1". La barra "0", de longitud <math>2\sqrt{2}L_0</math>, se articula en el punto <math>A</math> de la barra "2", mientras que su otro extremo desliza sobre el eje fijo <math>OX_1</math> con velocidad constante <math>\vec{v}_0</math>, como se indica en la figura. Las preguntas q…») |
Sin resumen de edición |
||
| Línea 9: | Línea 9: | ||
= Solución = | = Solución = | ||
== Vectores geométricos == | == Vectores geométricos y posiciones de los CIR== | ||
[[Archivo:BarrasCIRF1GIERMSCO2324.png|400px|derecha]] | [[Archivo:BarrasCIRF1GIERMSCO2324.png|400px|derecha]] | ||
Observando el dibujo tenemos | Observando el dibujo tenemos | ||
| Línea 17: | Línea 17: | ||
\overrightarrow{OA} = 2L_0\,\vec{\imath}_1 + 2L_0\,\vec{\jmath}_1,\\ | \overrightarrow{OA} = 2L_0\,\vec{\imath}_1 + 2L_0\,\vec{\jmath}_1,\\ | ||
\overrightarrow{AB} = L_0\,\vec{\imath}_1 - L_0\,\vec{\jmath}_1,\\ | \overrightarrow{AB} = L_0\,\vec{\imath}_1 - L_0\,\vec{\jmath}_1,\\ | ||
\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} = 3L_0\,\vec{\imath}_1 | \overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} = 3L_0\,\vec{\imath}_1 + L_0\,\vec{\jmath}_1. | ||
\end{array} | \end{array} | ||
</math> | |||
</center> | |||
En el dibujo también podemos ver la posición de los CIR. Tenemos que <math>B= I_{21}</math>, pues la barra "2" se articula en el sólido "1" en ese punto. También, <math>A= I_{20}</math> pues la barra "2" se articula en la barra "0" en ese punto. Por el teorema de los tres centros, el CIR <math>I_{01}</math> debe estar en la línea que une los otros dos CIR. Además, el punto <math>O</math> de la barra "0" se mueve deslizando sobre el eje <math>OX_1</math>. Por tanto, la velocidad <math>\vec{v}^{\,O}_{01}</math> es paralela a ese eje, y el CIR del movimiento {01} debe estar en la línea perpendicular a <math>\vec{v}^{\,O}_{01}</math> trazada por el punto <math>O</math>. El punto de corte se indica en la figura. | |||
Los vectores de posición son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\overrightarrow{OI}_{01} = 4L_0\,\vec{\jmath}_1,\\ | |||
\overrightarrow{OI}_{20} = \overrightarrow{OA} = 2L_0\,\vec{\imath}_1 + 2L_0\,\vec{\jmath}_1,\\ | |||
\overrightarrow{OI}_{21} = \overrightarrow{OB} = 3L_0\,\vec{\imath}_1 + L_0\,\vec{\jmath}_1,\\ | |||
\end{array} | |||
</math> | |||
</center> | |||
== Reducciones cinemáticas == | |||
Son todos movimientos planos. Por tanto los vectores rotación tienen la forma | |||
<center> | |||
<math> | |||
\vec{\omega}_{01} = \omega_{01}\,\vec{k}, \qquad \vec{\omega}_{20} = \omega_{20}\,\vec{k}, \qquad \vec{\omega}_{21} = \omega_{21}\,\vec{k}. | |||
</math> | |||
</center> | |||
Para el movimiento {01} tenemos la posición del CIR y la velocidad en el punto <math>O</math>. Usando el teorema de Chasles tenemos | |||
<center> | |||
<math> | |||
\vec{v}^{\,O}_{01} = \vec{\omega}_{01}\times\overrightarrow{I_01O} = (\omega_{01}\vec{k})\times(-4L_0\,\vec{\jmath}_1) | |||
= | |||
4\omega_{01}L_0\,\vec{\imath}_1. | |||
</math> | |||
</center> | |||
Como debe ser igual a <math>\vec{v}^{\,O}_{01}=v_0\,\vec{\imath}_1</math>, tenemos, para el movimiento {01} | |||
<center> | |||
<math> | |||
\vec{v}^{\,O}_{01} = v_0\,\vec{\imath}_1, \qquad \vec{\omega}_{01} = \dfrac{v_0}{4L_0}\,\vec{k}. | |||
</math> | |||
</center> | |||
Aplicamos la composición {21} = {20} + {01} en B. | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
\vec{v}^{\,B}_{21} = \vec{v}^{\,B}_{20} + \vec{v}^{\,B}_{01}.\\ | |||
\qquad \vec{v}^{\,B}_{21} = \vec{0}\\ | |||
\qquad \vec{v}^{\,B}_{20} = \vec{v}^{\,A}_{20} + \vec{\omega}_{20}\times\overrightarrow{AB} = \omega_{20}L_0\,\vec{\imath}_1 + \omega_{20}L_0\,\vec{\jmath}_1,\\ | |||
\\ | |||
\qquad \vec{v}^{\,B}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OB} = \dfrac{3}{4}v_0\,\vec{\imath}_1 + \dfrac{3}{4}v_0\,\vec{\jmath}_1. | |||
\end{array} | |||
</math> | |||
</center> | |||
Por tanto, para el movimiento {20} obtenemos | |||
<center> | |||
<math> | |||
\vec{v}^{\,A}_{20} = \vec{0}, \qquad \vec{\omega}_{20} = -\dfrac{3v_0}{4L_0}\,\vec{k}. | |||
</math> | |||
</center> | |||
Finalmente, usando <math>\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01}</math>, obtenemos para el movimiento {21} | |||
<center> | |||
<math> | |||
\vec{v}^{\,B}_{21} = \vec{0}, \qquad \vec{\omega}_{21} = -\dfrac{v_0}{2L_0}\,\vec{k}. | |||
</math> | |||
</center> | |||
== Aceleraciones == | |||
De la información del enunciado , sabemos que | |||
<center> | |||
<math> | |||
\vec{a}^{\,O}_{01} = \vec{0}, \qquad \vec{a}^{\,A}_{20} = \vec{0}, \qquad \vec{a}^{\,B}_{21} = \vec{0}. | |||
</math> | |||
</center> | |||
Son todos movimientos planos. Por tanto los vectores rotación tienen la forma | |||
<center> | |||
<math> | |||
\vec{\alpha}_{01} = \alpha_{01}\,\vec{k}, \qquad \vec{\alpha}_{20} = \alpha_{20}\,\vec{k}, \qquad \vec{\alpha}_{21} = \alpha_{21}\,\vec{k}. | |||
</math> | |||
</center> | |||
Aplicamos el Teorema de Coriolis en A | |||
<center> | |||
<math> | |||
\vec{a}^{\,A}_{21} = \vec{a}^{\,A}_{20} + \vec{a}^{\,A}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,A}_{20}. | |||
</math> | |||
</center> | |||
El primer y tercer términos en el lado derecho son nulos. Es decir | |||
<center> | |||
<math> | |||
\vec{a}^{\,A}_{21} = \vec{a}^{\,A}_{01}. | |||
</math> | |||
</center> | |||
La ecuación del campo de aceleraciones del movimiento {01} nos da | |||
<center> | |||
<math> | |||
\vec{a}^{\,A}_{01} = \vec{a}^{\,O}_{01} + \vec{\alpha}_{01}\times\overrightarrow{OA} - |\vec{\omega}_{01}|^2\overrightarrow{OA} | |||
= | |||
(-2\omega_0^2-2\alpha_{01})L_0\,\vec{\imath}_1 + (2\alpha_{01} -2\omega_0^2)L_0\,\vec{\jmath}_1. | |||
</math> | |||
</center> | |||
La ecuación del campo de aceleraciones del movimiento {21} nos da | |||
<center> | |||
<math> | |||
\vec{a}^{\,A}_{21} = \vec{a}^{\,B}_{21} + \vec{\alpha}_{21}\times\overrightarrow{BA} - |\vec{\omega}_{21}|^2\overrightarrow{BA} | |||
= | |||
(4\omega_0^2-\alpha_{21})L_0\,\vec{\imath}_1 + (-\alpha_{21} -4\omega_0^2)L_0\,\vec{\jmath}_1. | |||
</math> | |||
</center> | |||
En ambos casos hemos usado las velocidades angulares proporcionadas en el enunciado del tercer apartado. | |||
Igualando las componentes de los vectores obtenemos dos ecuaciones para dos incógnitas | |||
<center> | |||
<math> | |||
\left. | |||
\begin{array}{l} | |||
4\omega_0^2 - \alpha_{21} = -2\omega_0^2-2\alpha_{01},\\ | |||
-4\omega_0^2 - \alpha_{21} = -2\omega_0^2+ 2\alpha_{01}. | |||
\end{array} | |||
\right| | |||
\Longrightarrow | |||
\begin{array}{l} | |||
\vec{\alpha}_{21} = 2\omega_0^2\,\vec{k},\\ | |||
\vec{\alpha}_{01} = -2\omega_0^2\,\vec{k}. | |||
\end{array} | |||
</math> | |||
</center> | |||
Por último, usando la ley de composición de velocidades angulares para el movimiento plano tenemos | |||
<center> | |||
<math> | |||
\vec{\alpha}_{20} = \vec{\alpha}_{21} - \vec{\alpha}_{01} = 4\omega_0^2\,\vec{k}. | |||
</math> | </math> | ||
</center> | </center> | ||
Revisión actual - 12:43 28 jun 2024
Enunciado
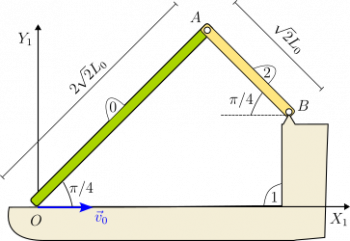
La barra "2", de longitud , está articulada en el punto fijo , perteneciente al sólido "1". La barra "0", de longitud , se articula en el punto de la barra "2", mientras que su otro extremo desliza sobre el eje fijo con velocidad constante , como se indica en la figura. Las preguntas que siguen se refieren al instante y los ángulos indicados en la figura.
- Escribe la expresión de los vectores , y .
- Encuentra la posición de los C.I.R. de los movimientos {01}, {20} y {21} por métodos gráficos y analíticos.
- Determina reducciones cinemáticas de los tres movimientos anteriores. Puedes elegir el punto en el que expresar estas reducciones.
- Suponiendo que , , calcula las aceleraciones angulares de los tres movimientos. (Estas no son las respuestas de la pregunta 3)
Solución
Vectores geométricos y posiciones de los CIR
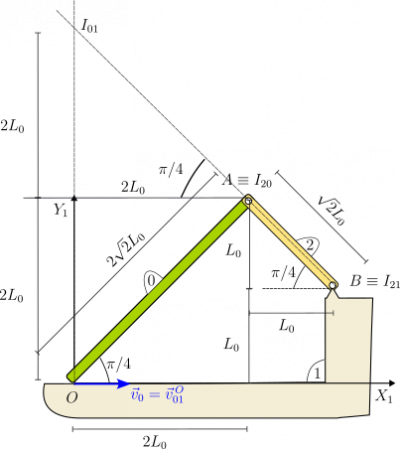
Observando el dibujo tenemos
En el dibujo también podemos ver la posición de los CIR. Tenemos que , pues la barra "2" se articula en el sólido "1" en ese punto. También, pues la barra "2" se articula en la barra "0" en ese punto. Por el teorema de los tres centros, el CIR debe estar en la línea que une los otros dos CIR. Además, el punto de la barra "0" se mueve deslizando sobre el eje . Por tanto, la velocidad es paralela a ese eje, y el CIR del movimiento {01} debe estar en la línea perpendicular a trazada por el punto . El punto de corte se indica en la figura.
Los vectores de posición son
Reducciones cinemáticas
Son todos movimientos planos. Por tanto los vectores rotación tienen la forma
Para el movimiento {01} tenemos la posición del CIR y la velocidad en el punto . Usando el teorema de Chasles tenemos
Como debe ser igual a , tenemos, para el movimiento {01}
Aplicamos la composición {21} = {20} + {01} en B.
Por tanto, para el movimiento {20} obtenemos
Finalmente, usando , obtenemos para el movimiento {21}
Aceleraciones
De la información del enunciado , sabemos que
Son todos movimientos planos. Por tanto los vectores rotación tienen la forma
Aplicamos el Teorema de Coriolis en A
El primer y tercer términos en el lado derecho son nulos. Es decir
La ecuación del campo de aceleraciones del movimiento {01} nos da
La ecuación del campo de aceleraciones del movimiento {21} nos da
En ambos casos hemos usado las velocidades angulares proporcionadas en el enunciado del tercer apartado. Igualando las componentes de los vectores obtenemos dos ecuaciones para dos incógnitas
Por último, usando la ley de composición de velocidades angulares para el movimiento plano tenemos

































