Movimiento de dos varillas articuladas

Enunciado

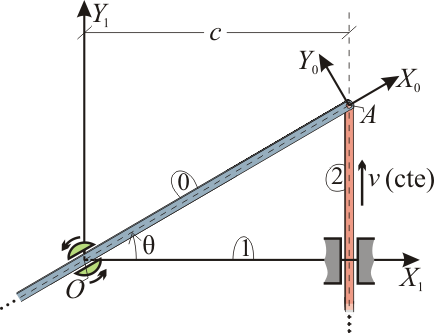
El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1Y_1} (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v} , manteniéndose siempre paralela al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OY_{\! 1}} y a una distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle c} de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto O del sólido “1”. Utilizando el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta} (definido en la figura) como parámetro descriptivo del movimiento, se pide:

1. Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\omega}_{21};\;\vec{v}^{\,O}_{21}\}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\omega}_{20};\;\vec{v}^{\,O}_{20}\}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\omega}_{01};\;\vec{v}^{\,O}_{01}\}} .
2. Determinación gráfica y determinación analítica de la posición del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I_{01}} , centro instantáneo de rotación del movimiento {01}.
3. Cálculo de las aceleraciones ${\vec {a}}_{01}^{A}$ y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^{\, O}_{01}} .

Nota: Para resolver el ejercicio, se propone el uso de la base vectorial asociada al sistema de ejes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle AX_{0}Y_0} de la figura, que se mueve solidariamente con la varilla “0” y cuyo eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle AX_{0}} es colineal con ella.

Reducciones cinemáticas

Las reducciones cinemáticas pueden hallarse sucesivamente, empezando por el movimiento más simple y empleando los resultados calculados para analizar los siguientes movimientos, más complejos. No obstante, en este caso, también pueden determinarse las tres reducciones simultáneamente considerando qué tipo de movimiento ocurre en cada caso.

Las tres simultáneamente

Debemos determinar tres velocidades angulares y tres velocidades lineales. Para determinarlas observamos que los tres movimientos se pueden clasificar como

Movimiento {21}

Este movimiento es una traslación, con una velocidad paralela al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OY_1} y de rapidez Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v} .

Movimiento {20}

Se trata de una rotación en torno al punto de articulación, A.

Movimiento {01}

Es una rotación en torno a un CIR cuya posición hemos de determinar.

Por tratarse de una traslación, la velocidad angular del movimiento {21} es nula. La del movimiento {01} la da la derivada del ángulo que forman los ejes respectivos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{21}=0\qquad\qquad \omega_{01}=\dot{\theta}}

Más adelante relacionaremos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}} con la rapidez Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v} dada en el enunciado.

La tercera velocidad angular la obtenemos empleando la fórmula de composición de velocidades angulares

$\omega _{20}=\omega _{21}+\omega _{10}=\omega _{21}-\omega _{01}=-{\dot {\theta }}$

También puede llegarse a ella derivando el ángulo que forman las dos barras, que es igual a $\pi /2-\theta$.

Para las velocidades lineales observamos que, por tratarse de una traslación, la velocidad de O en el movimiento {21} es la misma que la de A en dicho movimiento

${\vec {v}}_{21}^{O}={\vec {v}}_{21}^{A}=v{\vec {\jmath }}_{1}$

En el movimiento {20} el punto O se encuentra rotando en torno al punto A, por lo que su velocidad es perpendicular al vector de posición relativo

${\vec {v}}_{20}^{O}=\overbrace {\omega _{20}{\vec {k}}\times {\overrightarrow {AO}}} ^{\perp {\overrightarrow {AO}}}$

Puesto que el vector ${\overrightarrow {AO}}$ apunta en en la dirección de $OX_{0}$ esto nos da la dirección para la velocidad

${\vec {v}}_{20}^{O}=v_{20}^{O}{\vec {\jmath }}_{0}$

En el movimiento {01}, en cambio, el vínculo en el punto O obliga a que en este movimiento O se mueva a lo largo de la barra “0”, que es el eje $OX_{0}$. Por ello

${\vec {v}}_{01}^{O}=v_{01}^{O}{\vec {\imath }}_{0}$

Por otro lado, debe cumplirse la ley de composición de velocidades

${\vec {v}}_{21}^{O}={\vec {v}}_{20}^{O}+{\vec {v}}_{01}^{O}$

Sustituyendo los resultados anteriores

$v{\vec {\jmath }}_{1}=v_{20}^{O}{\vec {\jmath }}_{0}+v_{01}^{O}{\vec {\imath }}_{0}$

Podremos igualar las componentes respectivas si expresamos los dos miembros en la misma base.

$\left\{{\begin{array}{lcr}{\vec {\imath }}_{0}&=&\cos(\theta ){\vec {\imath }}_{1}+\mathrm {sen} (\theta ){\vec {\jmath }}_{1}\\{\vec {\jmath }}_{0}&=&-\mathrm {sen} (\theta ){\vec {\imath }}_{1}+\cos(\theta ){\vec {\jmath }}_{1}\end{array}}\right.$ ⇒ $\left\{{\begin{array}{lcr}{\vec {\imath }}_{1}&=&\cos(\theta ){\vec {\imath }}_{0}-\mathrm {sen} (\theta ){\vec {\jmath }}_{0}\\{\vec {\jmath }}_{1}&=&\mathrm {sen} (\theta ){\vec {\imath }}_{0}+\cos(\theta ){\vec {\jmath }}_{0}\end{array}}\right.$

Llevando esto a la ley de composición de velocidades

$v(\mathrm {sen} (\theta ){\vec {\imath }}_{0}+\cos(\theta ){\vec {\jmath }}_{0})=v_{20}^{O}{\vec {\jmath }}_{0}+v_{01}^{O}{\vec {\imath }}_{0}$ ⇒  $\left\{{\begin{array}{lcr}v_{20}^{O}&=&v\,\mathrm {cos} (\theta )\\v_{01}^{O}&=&v\,\mathrm {sen} (\theta )\end{array}}\right.$

y ya tenemos las tres velocidades.

Queda el relacionar ${\dot {\theta }}$ con $v$. Esto lo hacemos empleando trigonometría. La posición del punto A tiene la expresión

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OA}=c\vec{\imath}_1+c\,\mathrm{tg}(\theta)\vec{\jmath}_1}

Derivando esto respecto al tiempo e igualando con la velocidad que conocemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v\vec{\jmath}_1=\vec{v}^A_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OA}\right|_1 = \frac{c\dot{\theta}}{\cos^2(\theta)}\vec{\jmath}_1}

Despejamos de aquí

${\dot {\theta }}={\frac {v}{c}}\cos ^{2}(\theta )$

y con esto ya tenemos las tres reducciones cinemáticas.

Movimiento {21}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\omega}_{21},\vec{v}^O_{21}\right\}=\left\{\vec{0},v\vec{\jmath}_1\right\}}

Movimiento {01}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\omega}_{01},\vec{v}^O_{01}\right\}=\left\{\dot{\theta}\vec{k},v\,\mathrm{sen}(\theta)\vec{\imath}_0\right\}}

Movimiento {20}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\omega}_{20},\vec{v}^O_{20}\right\}=\left\{-\frac{v}{c}\cos^2(\theta)\vec{k},v\cos(\theta)\vec{\jmath}_0\right\}}

Las tres sucesivamente

Alternativamente, podemos analizar los movimientos en orden y obtener la reducción cinemática de cada uno

Movimiento {21}

La varilla “2” realiza una traslación respecto al sólido “1”, por tanto

$\omega _{21}=0\,$

La velocidad de esta traslación nos la da el enunciado, puesto que se nos dice que la barra sube con rapidez constante

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{21}=v\vec{\jmath}_1}

Esta velocidad la podemos obtener también derivando la posición de uno de los puntos del sólido “2”. El punto A, extremo de la barra, tiene un vector de posición instantáneo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OA}=c\vec{\imath}_1+c\,\mathrm{tg}(\theta)\vec{\jmath}_1}

Derivando en esta expresión

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OA}\right|_1 = \frac{c\dot{\theta}}{\cos^2(\theta)}\vec{\jmath}_1}

Igualando las dos expresiones obtenemos la relación

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}=\frac{v}{c}\cos^2(\theta)}

En el punto O la reducción es idéntica a la del punto A, por tratarse de una traslación. Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\omega}_{21},\vec{v}^O_{21}\right\}=\left\{\vec{0},v\vec{\jmath}_1\right\}}

Movimiento {01}

La velocidad angular del movimiento {01} la da la derivada del ángulo que forma el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0} con el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{01}=\dot{\theta}}

En términos de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v} , la rapidez de la barra

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{01}=\dot{\theta}=\frac{v}{c}\cos^2(\theta)}

La velocidad del punto O en este movimiento la obtenemos a partir de la velocidad del punto A, ya que, por tratarse de una articulación entre el sólido “2” y el “0”

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{01}=\overbrace{\vec{v}^A_{02}}^{=\vec{0}}+\vec{v}^A_{21} = v\vec{\jmath}_1}

La velocidad de O es entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{01}=\vec{v}^A_{01}+\omega_{01}\vec{k}\times\overrightarrow{AO}=v\vec{\jmath}_1+\frac{v}{c}\cos^2(\theta)\vec{k}\times\left(-c\vec{\imath}_1-c\,\mathrm{tg}(\theta)\vec{\jmath}_1\right)=v\,\mathrm{sen}(\theta)\cos(\theta)\vec{\imath}_1+v\,\mathrm{sen}^2(\theta)\vec{\jmath}_1}

Sacando factor común

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{01}=v\,\mathrm{sen}(\theta)\left(\cos(\theta)\vec{\imath}_1+\mathrm{sen}(\theta)\vec{\jmath}_1\right)}

El vector entre paréntesis no es otro que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}_0} , el unitario en la dirección del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0} , por lo cual

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{01}=v\mathrm{sen}(\theta)\vec{\imath}_0}

Esto está de acuerdo con que el par cinemático debido al pasador obliga a que la velocidad de O sea en la dirección de la propia barra en el movimiento {01}.

La reducción cinemática la escribimos reuniendo los dos resultados

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\omega}_{01},\vec{v}^O_{01}\right\}=\left\{\dot{\theta}\vec{k},v\,\mathrm{sen}(\theta)\vec{\imath}_0\right\}}

Movimiento {20}

Una vez que tenemos las otros dos reducciones cinemáticas, la del tercer movimiento se halla simplemente aplicando la ley de composición de velocidades angulares

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{20}=\omega_{21}+\omega_{10}=\omega_{21}-\omega_{01}=-\dot{\theta}=-\frac{v}{c}\cos^2(\theta)}

y la ley de composición de velocidades

${\vec {v}}_{20}^{O}={\vec {v}}_{21}^{O}+{\vec {v}}_{10}^{O}={\vec {v}}_{21}^{O}-{\vec {v}}_{01}^{O}=v{\vec {\jmath }}_{1}-v\,\mathrm {sen} (\theta ){\vec {\imath }}_{0}$

Esta expresión es correcta, pero no es muy informativa en cuanto a que mezcla vectores de dos bases diferentes. Pasando todo a la base “0”

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{20}=v\left(\mathrm{sen}(\theta)\vec{\imath}_0+\cos(\theta)\vec{\jmath}_0\right)-v\,\mathrm{sen}(\theta)\vec{\imath}_0=v\cos(\theta)\vec{\jmath}_0}

y, en la base “1”

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{20}=-v\,\mathrm{sen}(\theta)\cos(\theta)\vec{\imath}_1+v\cos^2(\theta)\vec{\jmath}_1}

lo que nos da la reducción cinemática

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\omega}_{20},\vec{v}^O_{20}\right\}=\left\{-\frac{v}{c}\cos^2(\theta)\vec{k},v\cos(\theta)\vec{\jmath}_0\right\}}

Podemos llegar a esta reducción directamente, sin emplear la composición de movimientos.

El ángulo que forman las dos barras es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \pi/2-\theta} por lo que la velocidad angular es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{20}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\pi}{2}-\theta\right)=-\dot{\theta}}

El movimiento {20} es una rotación en torno a la articulación A, que es el CIR Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I_{20}} . Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{20}=\omega_{20}\vec{k}\times\overrightarrow{AO}}

siendo el vector de posición relativo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{AO}=-c\vec{\imath}_1-c\,\mathrm{tg}(\theta)\vec{\jmath}_1 = -\frac{c}{\cos(\theta)}\vec{\imath}_0}

Sustituyendo este vector de posición y la velocidad angular reobtenemos el resultado anterior.

Posición del CIR

Gráficamente

Conocidas las direcciones de las velocidades Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{01}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^O_{01}} podemos localizar el CIR.

En el movimiento {01}, el punto A, según hemos visto, se mueve en la dirección del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OY_1} . Por tanto, el CIR Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I_{01}} se encuentra en la recta paralela a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1} que pasa por A.

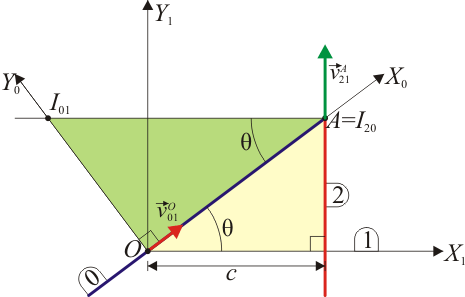
El punto O se encuentra obligado por el pasador a moverse longitudinalmente a lo largo del sólido “0”. Por ello, el CIR se encontrará en la perpendicular a la barra “0” que pasa por este punto.

La intersección de estas dos rectas nos da el CIR Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I_{01}} .

Su vector de posición lo obtenemos observando que se encuentra sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OY_0}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OI}_{01}=y_0 \vec{\jmath}_0}

La distancia sobre este eje es un cateto opuesto de un triángulo cuyo ángulo es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta} y cuyo cateto contiguo es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle |\overrightarrow{OA}|} . A su vez, esta distancia es una hipotenusa de otro triángulo cuyo cateto contiguo mide $c$:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(\theta)=\frac{y_0}{|\overrightarrow{OA}|}}     Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \cos(\theta)=\frac{c}{|\overrightarrow{OA}|}}

Despejando de aquí

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OI}_{01} = \frac{c\,\mathrm{sen}(\theta)}{\cos^2(\theta)}\vec{\jmath}_0}

Si expresamos este vector en la base ligada al sólido “1” nos da

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OI}_{01}=-c\,\mathrm{tg}^2(\theta)\vec{\imath}_1 + c\,\mathrm{tg}(\theta)\vec{\jmath}_1}

Analíticamente

También podemos obtener la posición del CIR conocida la reducción cinemática en O

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OI}_{01}=\frac{\vec{k}\times\vec{v}^O_{01}}{\omega_{01}}=\frac{c}{v\cos^2(\theta)}\vec{k}\times\left(v\,\mathrm{sen}(\theta)\vec{\imath}_0\right)=\frac{c\,\mathrm{sen}(\theta)}{\cos^2(\theta)}\vec{\jmath}_0}

que naturalmente coincide con el resultado anterior.

Aceleraciones

Del punto A

La aceleración del punto A es inmediata ya que, por tratarse de una articulación entre el sólido “2” y el “0” su movimiento {01} coincide con el {21}. En todo instante

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{01}=\overbrace{\vec{v}^A_{02}}^{=\vec{0}}+ \vec{v}^A_{21}=\vec{v}^A_{21}=v\vec{\jmath}_1}

y derivando aquí

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^A_{01}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\vec{v}^A_{01}\right|_1=\frac{\mathrm{d}v}{\mathrm{d}t}\vec{\jmath}_1=\vec{0}}

El movimiento de A es rectilíneo y uniforme tanto en el movimiento {21} como en el {01}.

Del punto O

Para hallar la aceleración de O en el movimiento {01} empleamos la expresión del campo de aceleraciones de un sólido, aprovechando que ya conocemos la de A

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^O_{01}=\vec{a}^A_{01}+\alpha_{01}\vec{k}\times\overrightarrow{AO}-\omega_{01}^2\overrightarrow{AO}}

donde

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_{01}=\dot{\theta}=\frac{v}{c}\cos^2(\theta)}

Derivando en esta expresión

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha_{01}=\ddot{\theta}=-2\frac{v}{c}\cos(\theta)\mathrm{sen}(\theta)\dot{\theta}=-2\frac{v^2}{c^2}\cos^3(\theta)\mathrm{sen}(\theta)}

El vector de posición relativo, en el sistema “0” posee solo componente en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{AO}=-\frac{c}{\cos(\theta)}\vec{\imath}_0}     Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{k}\times\overrightarrow{AO}=-\frac{c}{\cos(\theta)}\vec{\jmath}_0}

Llevando esto a la aceleración

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^A_{01}=\vec{0}+\left(-2\frac{v^2}{c^2}\cos^3(\theta)\mathrm{sen}(\theta)\right)\left(-\frac{c}{\cos(\theta)}\vec{\jmath}_0\right)-\left(\frac{v}{c}\cos^2(\theta)\right)^2\left(-\frac{c}{\cos(\theta)}\vec{\imath}_0\right) = \frac{v^2}{c}\cos^3(\theta)\vec{\imath}_0+2\frac{v^2}{c}\cos^2(\theta)\mathrm{sen}(\theta)\vec{\jmath}_0}

Extrayendo factores comunes

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^O_{01}=\frac{v^2}{c}\cos^2(\theta)\left(\cos(\theta)\vec{\imath}_0+2\mathrm{sen}(\theta)\vec{\jmath}_0\right)}