No Boletín - Placa triangular (Ex.Ene/16)

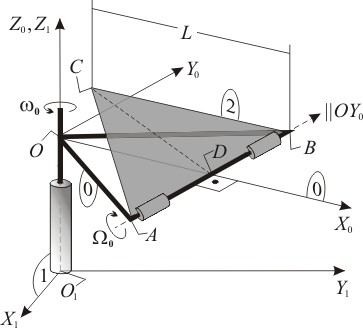
Enunciado

Una placa triangular $\,ABC\,$ (sólido "2"), equilátera de lado $\,L\,$, rota con velocidad angular constante $\,\Omega _{0}\,$ (en el sentido indicado en la figura) alrededor del lado $\,AB\,$ de un armazón triangular hueco $\,ABO\,$ (sólido "0") que tiene exactamente las mismas dimensiones que la placa. A su vez, el armazón $\,ABO\,$ se mantiene en todo instante en un plano horizontal paralelo al plano $\,O_{1}X_{1}Y_{1}\,$ del triedro fijo $\,O_{1}X_{1}Y_{1}Z_{1}\,$ (sólido "1"), y rota con velocidad angular constante $\,\omega _{0}\,$ (en el sentido indicado en la figura) alrededor del eje vertical fijo que pasa por su vértice $\,O\,$ (eje $\,O_{1}Z_{1}\,$). Sea $\,\{{\vec {\imath }}_{0},{\vec {\jmath }}_{0},{\vec {k}}_{0}\}\,$ la base ortonormal asociada al triedro $\,OX_{0}Y_{0}Z_{0}\,$ (sólido "0") definido en la figura, el cual se mueve solidariamente con el armazón triangular $\,ABO.\,$

Determine las siguientes magnitudes:

1. Velocidad $\,{\vec {v}}_{21}^{\,D}\,$ (ver $\,D\,$ en la figura)
2. Aceleración angular $\,{\vec {\alpha }}_{21}\,$
3. Aceleración $\,{\vec {a}}_{21}^{\,O}\,$

Caracterización de los movimientos elementales {01} y {20}

Los datos del enunciado nos permiten expresar en la base vectorial $\{{\vec {\imath }}_{0},{\vec {\jmath }}_{0},{\vec {k}}_{0}\}\,$ las reducciones cinemáticas del movimiento $\{01\}\,$ (en el punto $O\,$) y del movimiento $\{20\}\,$ (en el punto $D\!\,$), así como un par de vectores geométricos que necesitaremos más adelante:

$\left\{{\begin{array}{l}{\vec {\omega }}_{01}(t)=\omega _{0}\,{\vec {k}}_{0}\\\\{\vec {v}}_{01}^{\,O}(t)={\vec {0}}\end{array}}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{{\begin{array}{l}{\vec {\omega }}_{20}(t)=\Omega _{0}\,{\vec {\jmath }}_{0}\\\\{\vec {v}}_{20}^{\,D}(t)={\vec {0}}\end{array}}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left|{\begin{array}{l}{\overrightarrow {OD}}=\displaystyle {\frac {\sqrt {3}}{2}}L\,\,{\vec {\imath }}_{0}\\\\{\overrightarrow {DO}}=-\,{\overrightarrow {OD}}=-\,\displaystyle {\frac {\sqrt {3}}{2}}L\,\,{\vec {\imath }}_{0}\end{array}}\right.$

habiéndose tenido en cuenta que el punto $O\,$ es un punto fijo en el movimiento $\{01\}\,$ porque pertenece a su eje permanente de rotación (eje $O_{1}Z_{1}\,$), y que el punto $D\,$ es un punto fijo en el movimiento $\{20\}\,$ porque pertenece a su eje permanente de rotación (recta que pasa por los puntos $\,A\,$ y $\,B\,$).

Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos $\{01\}\,$ y $\{20\}\,$ las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante:

$\left|{\begin{array}{l}{\vec {\alpha }}_{01}=\displaystyle \left.{\frac {\mathrm {d} {\vec {\omega }}_{01}}{\mathrm {d} t}}\right|_{1}\!=\displaystyle \left.{\frac {\mathrm {d} (\omega _{0}\,{\vec {k}}_{0})}{\mathrm {d} t}}\right|_{1}\!=\displaystyle \left.{\frac {\mathrm {d} (\omega _{0}\,{\vec {k}}_{1})}{\mathrm {d} t}}\right|_{1}\!={\vec {0}}\\\\{\vec {a}}_{01}^{\,O}=\displaystyle \left.{\frac {\mathrm {d} {\vec {v}}_{01}^{\,O}}{\mathrm {d} t}}\right|_{1}\!=\displaystyle \left.{\frac {\mathrm {d} {\vec {0}}}{\mathrm {d} t}}\right|_{1}\!={\vec {0}}\end{array}}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left|{\begin{array}{l}{\vec {\alpha }}_{20}=\displaystyle \left.{\frac {\mathrm {d} {\vec {\omega }}_{20}}{\mathrm {d} t}}\right|_{0}\!=\displaystyle \left.{\frac {\mathrm {d} (\Omega _{0}\,{\vec {\jmath }}_{0})}{\mathrm {d} t}}\right|_{0}\!={\vec {0}}\\\\{\vec {a}}_{20}^{\,D}=\displaystyle \left.{\frac {\mathrm {d} {\vec {v}}_{20}^{\,D}}{\mathrm {d} t}}\right|_{0}\!=\displaystyle \left.{\frac {\mathrm {d} {\vec {0}}}{\mathrm {d} t}}\right|_{0}\!={\vec {0}}\end{array}}\right.$

Velocidad {21} del punto D

Para determinar la velocidad ${\vec {v}}_{21}^{\,D}\,$, calculamos primero la velocidad ${\vec {v}}_{01}^{\,D}\,$ utilizando la ecuación del campo de velocidades $\,\{01\}\,$:

${\begin{array}{l}{\vec {v}}_{01}^{\,D}=\displaystyle \underbrace {{\vec {v}}_{01}^{\,O}} _{\displaystyle {\vec {0}}}+\,\,{\vec {\omega }}_{01}\times {\overrightarrow {OD}}=\omega _{0}\,{\vec {k}}_{0}\times \displaystyle {\frac {\sqrt {3}}{2}}L\,\,{\vec {\imath }}_{0}=\displaystyle {\frac {\sqrt {3}}{2}}\,\omega _{0}L\,{\vec {\jmath }}_{0}\end{array}}$

y, a continuación, aplicamos la ley de composición de velocidades en el punto $D\,$:

${\vec {v}}_{21}^{\,D}=\underbrace {{\vec {v}}_{20}^{\,D}} _{\displaystyle {\vec {0}}}+\,\,{\vec {v}}_{01}^{\,D}=\displaystyle {\frac {\sqrt {3}}{2}}\,\omega _{0}L\,{\vec {\jmath }}_{0}$

Aceleración angular {21}

Determinamos la aceleración angular ${\vec {\alpha }}_{21}\,$ aplicando la ley de composición de aceleraciones angulares:

${\vec {\alpha }}_{21}=\underbrace {{\vec {\alpha }}_{20}} _{\displaystyle {\vec {0}}}+\underbrace {{\vec {\alpha }}_{01}} _{\displaystyle {\vec {0}}}+\,\,{\vec {\omega }}_{01}\times {\vec {\omega }}_{20}=\omega _{0}\,{\vec {k}}_{0}\times \Omega _{0}\,{\vec {\jmath }}_{0}=\,-\,\omega _{0}\,\Omega _{0}\,{\vec {\imath }}_{0}$

Aceleración {21} del punto O

La ley de composición de aceleraciones (teorema de Coriolis) nos permite calcular la aceleración ${\vec {a}}_{21}^{\,O}\,$:

${\vec {a}}_{21}^{\,O}={\vec {a}}_{20}^{\,O}+{\vec {a}}_{01}^{\,O}+2\,{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{\,\,O}$

Determinamos, primero, la aceleración ${\vec {a}}_{20}^{\,O}\,$ (mediante la ecuación del campo de aceleraciones $\{20\}\,$):

$\,\,\,\,\,{\vec {a}}_{20}^{\,O}=\underbrace {{\vec {a}}_{20}^{\,D}} _{\displaystyle {\vec {0}}}+\,\underbrace {{\vec {\alpha }}_{20}} _{\displaystyle {\vec {0}}}\times \,{\overrightarrow {DO}}\,+\,\,{\vec {\omega }}_{20}\,\times \,(\omega _{20}\,\times \,{\overrightarrow {DO}})=\Omega _{0}\,{\vec {\jmath }}_{0}\,\times \,\left[\,\Omega _{0}\,{\vec {\jmath }}_{0}\,\times \,\left(-{\frac {\sqrt {3}}{2}}L\,\,{\vec {\imath }}_{0}\right)\right]=$

$\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\Omega _{0}\,{\vec {\jmath }}_{0}\,\times \,{\frac {\sqrt {3}}{2}}\Omega _{0}L\,{\vec {k}}_{0}=\displaystyle {\frac {\sqrt {3}}{2}}\,\Omega _{0}^{2}\,L\,{\vec {\imath }}_{0}$

y, a continuación, el término de Coriolis:

$2\,{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{\,O}=2\,{\vec {\omega }}_{01}\times (\underbrace {{\vec {v}}_{20}^{\,D}} _{\displaystyle {\vec {0}}}+\,\,{\vec {\omega }}_{20}\times {\overrightarrow {DO}})=2\,\omega _{0}\,{\vec {k}}_{0}\times {\frac {\sqrt {3}}{2}}\Omega _{0}L\,{\vec {k}}_{0}={\vec {0}}$

Sustituyendo en la ley de composición de aceleraciones, obtenemos por fin la aceleración ${\vec {a}}_{21}^{\,O}\,$:

${\vec {a}}_{21}^{\,O}={\vec {a}}_{20}^{\,O}+\underbrace {{\vec {a}}_{01}^{\,O}} _{\displaystyle {\vec {0}}}+\underbrace {2\,{\vec {\omega }}_{01}\!\times {\vec {v}}_{20}^{\,O}} _{\displaystyle {\vec {0}}}=\displaystyle {\frac {\sqrt {3}}{2}}\,\Omega _{0}^{2}L\,{\vec {\imath }}_{0}$