No Boletín - Placa triangular (Ex.Ene/16)

Enunciado

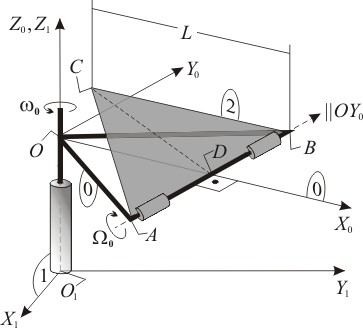
Una placa triangular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,ABC\,} (sólido "2"), equilátera de lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,L\,} , rota con velocidad angular constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\Omega_0\,} (en el sentido indicado en la figura) alrededor del lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,AB\,} de un armazón triangular hueco Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,ABO\,} (sólido "0") que tiene exactamente las mismas dimensiones que la placa. A su vez, el armazón Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,ABO\,} se mantiene en todo instante en un plano horizontal paralelo al plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O_1X_1Y_1\,} del triedro fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O_1X_1Y_1Z_1\,} (sólido "1"), y rota con velocidad angular constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\omega_0\,} (en el sentido indicado en la figura) alrededor del eje vertical fijo que pasa por su vértice Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O\,} (eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,O_1Z_1\,} ). Sea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\{\vec{\imath}_0,\vec{\jmath}_0, \vec{k}_0\}\,} la base ortonormal asociada al triedro Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,OX_0Y_0Z_0\,} (sólido "0") definido en la figura, el cual se mueve solidariamente con el armazón triangular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,ABO.\,}

Determine las siguientes magnitudes:

1. Velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\vec{v}^{\, D}_{21}\,} (ver Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,D\,} en la figura)
2. Aceleración angular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\vec{\alpha}_{21}\,}
3. Aceleración Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\vec{a}^{\, O}_{21}\,}

Caracterización de los movimientos elementales {01} y {20}

Los datos del enunciado nos permiten expresar en la base vectorial Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\imath}_0,\vec{\jmath}_0,\vec{k}_0\}\,} las reducciones cinemáticas del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{01\}\,} (en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} ) y del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{20\}\,} (en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle D\!\,} ), así como un par de vectores geométricos que necesitaremos más adelante:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left\{\begin{array}{l} \vec{\omega}_{01}(t)=\omega_0\,\vec{k}_0 \\ \\ \vec{v}^{\, O}_{01}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left\{\begin{array}{l} \vec{\omega}_{20}(t)=\Omega_0\,\vec{\jmath}_0 \\ \\ \vec{v}^{\, D}_{20}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left|\begin{array}{l} \overrightarrow{OD}=\displaystyle\frac{\sqrt{3}}{2}L\,\,\vec{\imath}_0 \\ \\ \overrightarrow{DO}=-\,\overrightarrow{OD}=-\,\displaystyle\frac{\sqrt{3}}{2}L\,\,\vec{\imath}_0 \end{array}\right. }

habiéndose tenido en cuenta que el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O\,} es un punto fijo en el movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{01\}\,} porque pertenece a su eje permanente de rotación (eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O_1Z_1\,} ), y que el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle D\,} es un punto fijo en el movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{20\}\,} porque pertenece a su eje permanente de rotación (recta que pasa por los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,A\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,B\,} ).

Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{01\}\,} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{20\}\,} las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left|\begin{array}{l} \vec{\alpha}_{01}=\displaystyle\left.\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1\! =\displaystyle\left.\frac{\mathrm{d}(\omega_0\,\vec{k}_0)}{\mathrm{d}t}\right|_1\! =\displaystyle\left.\frac{\mathrm{d}(\omega_0\,\vec{k}_1)}{\mathrm{d}t}\right|_1\! =\vec{0} \\ \\ \vec{a}^{\, O}_{01}=\displaystyle\left.\frac{\mathrm{d}\vec{v}^{\, O}_{01}}{\mathrm{d}t}\right|_1\! =\displaystyle\left.\frac{\mathrm{d}\vec{0}}{\mathrm{d}t}\right|_1\! =\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left|\begin{array}{l} \vec{\alpha}_{20}=\displaystyle\left.\frac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0\! =\displaystyle\left.\frac{\mathrm{d}(\Omega_0\,\vec{\jmath}_0)}{\mathrm{d}t}\right|_0\! =\vec{0} \\ \\ \vec{a}^{\, D}_{20}=\displaystyle\left.\frac{\mathrm{d}\vec{v}^{\, D}_{20}}{\mathrm{d}t}\right|_0\! =\displaystyle\left.\frac{\mathrm{d}\vec{0}}{\mathrm{d}t}\right|_0\! =\vec{0} \end{array}\right. }

Velocidad {21} del punto D

Para determinar la velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\, D}_{21}\,} , calculamos primero la velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\, D}_{01}\,} utilizando la ecuación del campo de velocidades Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\{01\}\,} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{v}^{\, D}_{01}=\displaystyle\underbrace{\vec{v}^{\, O}_{01}}_{\displaystyle\vec{0}}+\,\,\vec{\omega}_{01}\times\overrightarrow{OD}=\omega_0\,\vec{k}_0\times \displaystyle\frac{\sqrt{3}}{2}L\,\,\vec{\imath}_0=\displaystyle\frac{\sqrt{3}}{2}\,\omega_0 L\,\vec{\jmath}_0 \end{array} }

y, a continuación, aplicamos la ley de composición de velocidades en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle D\,} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\, D}_{21}=\underbrace{\vec{v}^{\, D}_{20}}_{\displaystyle\vec{0}}+\,\,\vec{v}^{\, D}_{01}=\displaystyle\frac{\sqrt{3}}{2}\,\omega_0 L\,\vec{\jmath}_0 }

Aceleración angular {21}

Determinamos la aceleración angular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\alpha}_{21}\,} aplicando la ley de composición de aceleraciones angulares:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\alpha}_{21}=\underbrace{\vec{\alpha}_{20}}_{\displaystyle\vec{0}}+\underbrace{\vec{\alpha}_{01}}_{\displaystyle\vec{0}}+\,\,\vec{\omega}_{01}\times\vec{\omega}_{20}=\omega_0\,\vec{k}_0\times \Omega_0\,\vec{\jmath}_0=\,-\,\omega_0\,\Omega_0\,\vec{\imath}_0 }

Aceleración {21} del punto O

La ley de composición de aceleraciones (teorema de Coriolis) nos permite calcular la aceleración Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^{\, O}_{21}\,} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^{\, O}_{21}=\vec{a}^{\, O}_{20}+\vec{a}^{\, O}_{01}+2\,\vec{\omega}_{01}\times\vec{v}^{\,\, O}_{20} }

Determinamos, primero, la aceleración Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^{\, O}_{20}\,} (mediante la ecuación del campo de aceleraciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{20\}\,} ):

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\,\,\,\,\vec{a}^{\, O}_{20}=\underbrace{\vec{a}^{\, D}_{20}}_{\displaystyle\vec{0}}+\,\underbrace{\vec{\alpha}_{20}}_{\displaystyle\vec{0}}\times\,\overrightarrow{DO}\,+\,\,\vec{\omega}_{20}\,\times\,(\omega_{20}\,\times\,\overrightarrow{DO})=\Omega_0\,\vec{\jmath}_0\,\times\,\left[\,\Omega_0\,\vec{\jmath}_0\,\times\,\left(-\frac{\sqrt{3}}{2}L\,\,\vec{\imath}_0\right)\right]=}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \,\,\,\,\,\,\,\,\,\,\,\,=\Omega_0\,\vec{\jmath}_0\,\times\,\frac{\sqrt{3}}{2}\Omega_0 L\,\vec{k}_0=\displaystyle\frac{\sqrt{3}}{2}\,\Omega_0^2\, L\,\vec{\imath}_0 }

y, a continuación, el término de Coriolis:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2\,\vec{\omega}_{01}\times\vec{v}^{\, O}_{20}=2\,\vec{\omega}_{01}\times(\underbrace{\vec{v}^{\, D}_{20}}_{\displaystyle\vec{0}}+\,\,\vec{\omega}_{20}\times\overrightarrow{DO})=2\,\omega_0\,\vec{k}_0\times\frac{\sqrt{3}}{2}\Omega_0 L\,\vec{k}_0=\vec{0} }

Sustituyendo en la ley de composición de aceleraciones, obtenemos por fin la aceleración Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^{\, O}_{21}\,} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^{\, O}_{21}=\vec{a}^{\, O}_{20}+\underbrace{\vec{a}^{\, O}_{01}}_{\displaystyle\vec{0}}+\underbrace{2\,\vec{\omega}_{01}\!\times\vec{v}^{\, O}_{20}}_{\displaystyle\vec{0}}=\displaystyle\frac{\sqrt{3}}{2}\,\Omega_0^2 L\,\vec{\imath}_0 }