Diferencia entre revisiones de «Problemas de cinemática del movimiento relativo (CMR)»
| Línea 50: | Línea 50: | ||
</table> | </table> | ||
[[Velocidad relativa de dos vagones|Solución]] | [[Velocidad relativa de dos vagones|Solución]] | ||
==Peonza rodante oblicua== | |||
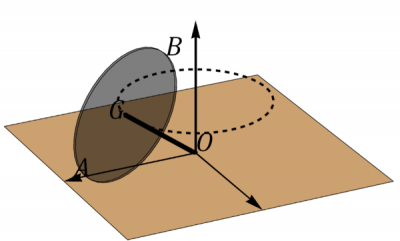
Una peonza está formada por una varilla de longitud <math>\ell=20\,\mathrm{cm}</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez <math>v_0=48\,\mathrm{cm/s}</math>. El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula. | |||
Para este movimiento, determine, en el instante en que A se encuentra sobre el eje OX: | |||
# La velocidad angular del sólido en el movimiento {21}. | |||
# La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en <math>25\vec{k}\,\mathrm{cm}</math>, considerado como punto del sólido. | |||
# La aceleración angular del sólido. | |||
# La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido. | |||
<center>[[Archivo:Peonza-rodante.png|400px]]</center> | |||
[[Peonza rodante oblicua (CMR)|Solución]] | |||
Revisión del 00:31 23 nov 2023
Rotaciones finitas sucesivas de 90°
Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a . ¿Cuál es la matriz de rotación que permite pasar de las coordenadas (X,Y,Z) en la posición final del sistema ligado a las coordenadas en el sistema fijo (x,y,z)? ¿Cuál es el eje de rotación de la composición? ¿Cuál es el ángulo girado?
- ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a ?
- ¿Cómo cambian los resultados anteriores si, partiendo de la posición inicial se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a ?
- Si se realizan las dos rotaciones del apartado (a) (1º +90° en torno a ; 2º +90° en torno a ) y a continuación se gira −90° en torno a seguido de −90° en torno a , ¿vuelve el sólido a su posición inicial? Si no es así, ¿cuál es el eje de rotación y el ángulo girado?
Rotaciones finitas sucesivas
¿Cómo quedan los resultados del problema anterior si los giros no son de +90° sino de ? (recomendable hacer los cálculos con ayuda de un ordenador).
Composición de dos rotaciones de 90°
Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación −90° en torno a un eje paralelo a por . ¿Cuál es el resultado de esta composición de movimientos?
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación +90° en torno a un eje paralelo a por . ¿Cuál es el resultado de esta composición de movimientos?
- Supongamos que el sólido se hace girar en primer lugar +90° en torno a y a continuación −90° en torno a un eje paralelo a por . ¿Cuál es el resultado de esta composición de movimientos?
Velocidad relativa de dos vagones
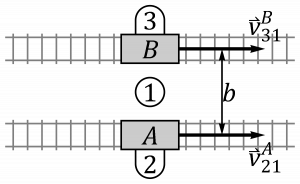
Se tienen dos vagonetas A y B (sólidos “2” y “3”), que avanzan por raíles sobre el suelo horizontal (sólido “1”). En un momento dado las vagonetas se mueven paralelamente respecto al suelo con velocidades . El vector de posición relativo entre las dos vagonetas es . Los ejes de los tres sistemas se toman paralelos de forma que los vectores de las respectivas bases son coincidentes en ese instante. Halle las velocidades relativas y en los siguientes casos:
- Las vagonetas se mueven por vías rectilíneas paralelas.
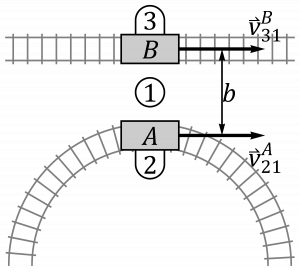
- La vagoneta B se mueve por una vía circular de radio R, mientras que A se mueve por una vía rectilínea. El instante descrito es el de máximo acercamiento entre las dos vías.
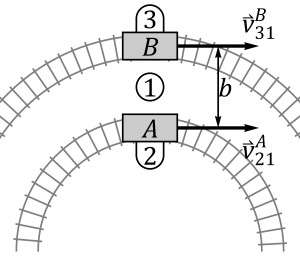
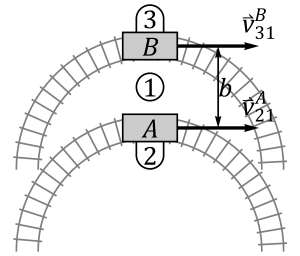
- Las dos se mueven por vías circulares concéntricas, de radios R y R+b, respectivamente.
- Las dos se mueven por arcos de circunferencia de radio R con centros hacia el mismo lado.
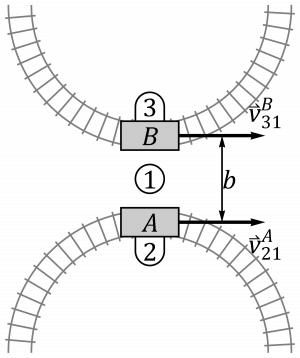
- Las dos se mueven por arcos de circunferencia de radio R con centros en lados opuestos.
 |
 |
 |
| (1) | (2) | |
|---|---|---|
 |
 |
|
| (3) | (4) | (5) |
Peonza rodante oblicua
Una peonza está formada por una varilla de longitud ensartada en un disco de radio . Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez . El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula. Para este movimiento, determine, en el instante en que A se encuentra sobre el eje OX:
- La velocidad angular del sólido en el movimiento {21}.
- La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en , considerado como punto del sólido.
- La aceleración angular del sólido.
- La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido.