Diferencia entre revisiones de «No Boletín - Péndulo cónico (Ex.Ene/13)»
(Página creada con «==Enunciado== right Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un movimiento circular uniforme en un plano horizontal (ver figura). Considere que la masa puntual es <math>m\,</math>, la longitud del péndulo es <math>L\,</math>, el ángulo que forma el hilo con la vertical es <math>\theta\,</math> y la gravedad es <math>g\,</math>. # ¿Con qué celeridad se mue…») |
Sin resumen de edición |
||
| Línea 42: | Línea 42: | ||
</math></center> | </math></center> | ||
[[Categoría:Problemas de | [[Categoría:Problemas de Dinámica del Punto (GITI)]] | ||
Revisión actual - 19:08 10 ene 2024
Enunciado
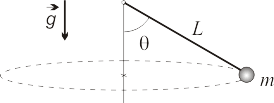
Se denomina péndulo cónico a un péndulo simple cuya masa puntual, en lugar de oscilar en un plano vertical, realiza un movimiento circular uniforme en un plano horizontal (ver figura). Considere que la masa puntual es , la longitud del péndulo es , el ángulo que forma el hilo con la vertical es y la gravedad es .
- ¿Con qué celeridad se mueve la masa puntual?
- ¿Cuál es el módulo de la tensión del hilo?
Solución
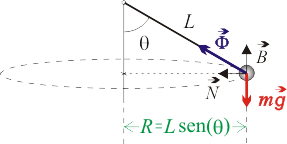
La masa puntual describe con celeridad constante (movimiento uniforme) una circunferencia de radio:
y lo hace bajo la acción de dos fuerzas: el peso y la tensión ejercida por el hilo .
Para expresar las magnitudes vectoriales, utilizaremos el triedro intrínseco de la circunferencia.
El peso es una fuerza activa y, como tal, es conocida a priori:
Sin embargo, la tensión del hilo es una fuerza de reacción vincular, de módulo en principio desconocido, con dirección a lo largo del hilo y sentido hacia el punto de suspensión del hilo:
Dado que la masa puntual describe un movimiento circular uniforme, sabemos que su aceleración sólo va a tener componente normal:
Aplicando la segunda ley de Newton, y separando componentes, se llega al siguiente sistema de ecuaciones (para las incógnitas y ):
Resolviendo el sistema, obtenemos los valores de la celeridad de la partícula y del módulo de la tensión del hilo:











![{\displaystyle {\vec {\Phi }}=\Phi [\,\mathrm {sen} (\theta )\,{\vec {N}}+\mathrm {cos} (\theta )\,{\vec {B}}\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32420bd5b876dadc582ff996a54c974c45bea65f)


