Sistemas simples de sólidos rígidos

Introducción

Las aplicaciones de la dinámica del sólido rígido son incalculables ya que gran parte de la teoría de máquinas y mecanismos puede realizarse suponiendo que los distintos componentes son aproximadamente rígidos. La mayoría de estas aplicaciones, incluso las de apariencia sencilla, no obstante, suele implicar complejos cálculos matemáticos, por lo que escapan al alcance de esta introducción.

Ley de la palanca

La ley de la palanca es una aplicación conocida desde la antigüedad de la dinámica de sólidos rígidos,.

En su versión más simple consiste en una palanca (una plataforma, por ejemplo) apoyada sobre un punto O (el fulcro) en torno al cual puede girar.

A un lado del fulcro y a una distancia $d_{A}$ de él se aplica una fuerza ${\vec {F}}_{A}$ (denominada, por razones históricas, la potencia). A una distancia $d_{B}$ al otro lado del fulcro se encuentra una carga que ejerce una fuerza ${\vec {F}}_{B}$ (la resistencia), que debe vencerse con ayuda de la palanca. La pregunta es ¿cuál es la mínima potencia que debe aplicarse para vencer una resistencia dada?

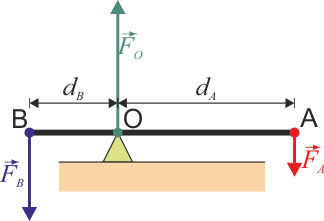
Tomando como eje OX el tangente a la palanca, OY el vertical hacia arriba, y con origen en el fulcro, la potencia y la resistencia las suponemos hacia abajo

${\vec {F}}_{A}=-F_{A}{\vec {\jmath }}\qquad \qquad {\vec {F}}_{B}=-F_{B}{\vec {\jmath }}$

La potencia mínima es aquella que consigue equilibrar la palanca, lo cual implica que se anula tanto la resultante como el momento resultante respecto a un punto arbitrario. Por comodidad elegimos el propio punto O.

${\vec {F}}={\vec {0}}\qquad \qquad {\vec {M}}_{O}={\vec {0}}$

A la hora de considerar la resultante de las fuerzas también hay que incluir la reacción del fulcro.

${\vec {F}}={\vec {0}}\qquad \Rightarrow \qquad {\vec {F}}_{O}=-{\vec {F}}_{A}-{\vec {F}}_{B}=(F_{A}+F_{B}){\vec {\jmath }}$

Es decir, el fulcro soporta la acción combinada de la potencia y la resistencia, por lo que si estas son demasiado elevadas (se trata de levantar una gran carga, por ejemplo) puede vencerse el límite de resistencia y romperse el sistema.

El momento respecto al fulcro es nulo

${\vec {0}}={\vec {M}}_{O}={\overrightarrow {OA}}\times {\vec {F}}_{A}+{\overrightarrow {OB}}\times {\vec {F}}_{B}$

Desarrollando en componentes cartesianas,

${\vec {0}}=(d_{A}{\vec {\imath }})\times (-F_{A}{\vec {\jmath }})+(-d_{B}{\vec {\imath }})\times (-F_{B}{\vec {\jmath }})=\left(-d_{A}F_{A}+d_{B}F_{B}\right){\vec {k}}$

de donde obtenemos la relación

$-d_{A}F_{A}+d_{B}F_{B}=0\qquad \Rightarrow \qquad d_{A}F_{A}=d_{B}F_{B}$

que se enuncia como el producto de la potencia por su brazo es igual al de la resistencia por el suyo (ley de la palanca). Técnicamente nos dice que el par ejercido por una de las fuerzas sobre la palanca debe compensar el ejercido por la otra.

Por la tercera ley de Newton, si la resistencia ejerce una fuerza ${\vec {F}}_{B}$ sobre la palanca, ésta ejerce una fuerza $-{\vec {F}}_{B}$ sobre la carga. Esto nos dice que en una situación de equilibrio, al ejercer una fuerza ${\vec {F}}_{A}$ en la posición de la potencia se transmite una fuerza $-{\vec {F}}_{B}$ en la posición de la resistencia. Esta segunda fuerza podrá ser mayor o menor que la primera, dependiendo de la longitud de los respectivos brazos.

Por sus aplicaciones técnicas, las palancas se califican en tres tipos:

Palanca de primera especie

Es la que tiene la potencia a un lado del fulcro y la resistencia al otro

Una potencia hacia abajo resulta en un empuje hacia arriba en la resistencia. La magnitud de la fuerza sobre la resistencia es

$F_{B}={\frac {d_{A}}{d_{B}}}F_{A}$

Si $d_{A}>d_{B}$ la fuerza transmitida a la resistencia es superior a la ejercida sobre la potencia. Eligiendo el brazo de la potencia lo largo que sea necesario es posible vencer (teóricamente) cualquier resistencia y levantar cualquier objeto.

Palanca de segunda especie

Es aquella en la que la resistencia se encuentra entre la potencia y el fulcro.

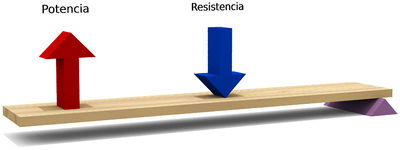
En ella la fuerza sobre la resistencia va en el mismo sentido que la potencia ejercida, pero es de mayor magnitud (ya que necesariamente $|d_{B}|<|d_{A}|$). Ejemplos de palancas de segunda especie serían un cascanueces, una carretilla o los remos de una piragua (cuyo punto de apoyo es el agua).

Palanca de tercera especie

Es aquella en la que la potencia se encuentre entre la resistencia y el fulcro.

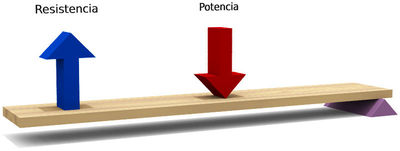
En ella la fuerza sobre la resistencia va en el mismo sentido que la potencia ejercida, siendo ahora de menor magnitud (ya que $|d_{B}|>|d_{A}|$). Una palanca de tercera especie interesa cuando se desea multiplicar el desplazamiento de la carga o su velocidad. Un ejemplo de palanca de tercera especie es la mandíbula humana.

Tanto en la palanca de primera especie cuando $d_{B}<d_{A}$ como en la de segunda especie, la resistencia que se vence es superior a la potencia. Con ayuda de una palanca seríamos capaces de levantar un piano de cola simplemente apretando con el pulgar, o de romper una barra de acero con un cascanueces.

Parece que esto violaría alguna ley de conservación, pues estaríamos obteniendo fuerza “gratis”. La clave es la respuesta a la pregunta ¿cuánto levantaríamos el piano? Si empujando en la potencia realizamos un desplazamiento $\mathrm {d} z_{1}$ esto quiere decir que la palanca gira un ángulo

$\mathrm {d} \theta ={\frac {\mathrm {d} s}{R}}={\frac {\mathrm {d} z_{A}}{d_{A}}}$

Este giro se traduce en una elevación en la resistencia

$\mathrm {d} z_{B}=d_{B}\mathrm {d} \theta ={\frac {d_{B}}{d_{A}}}\mathrm {d} z_{1}$

es decir, el desplazamiento en la resistencia será menor que el de la potencia. El trabajo realizado sobre la resistencia es igual a

$\delta W_{B}=F_{B}\mathrm {d} z_{B}=\left({\frac {d_{A}}{d_{B}}}F_{A}\right)\left({\frac {d_{B}}{d_{A}}}\mathrm {d} z_{A}\right)=F_{A}\,\mathrm {d} z_{A}=\delta W_{A}$

con lo que el trabajo que se realiza por un lado es el que se saca por el otro, con lo que no se viola la ley de conservación de la energía.

Vuelco inminente

Al modelar el comportamiento de un sólido como una partícula, la única posibilidad que se considera es si se desplaza o no. Si tenemos un bloque encima de un plano horizontal y aplicamos una fuerza también horizontal sobre él, solo nos planteábamos si el bloque comenzaba a moverse o no. Para ello, la única condición es que la fuerza aplicada superara el límite de deslizamiento inminente. Dado que la fuerza de rozamiento estático verifica

$|{\vec {F}}_{r}|\leq \mu |{\vec {F}}_{n}|$

y en el caso de un bloque horizontal

$|{\vec {F}}_{n}|=Mg$

obtenemos la condición

$|{\vec {F}}_{r}|\leq \mu Mg$

según la cual si la fuerza aplicada es menor que $\mu Mg$ el bloque quedará en reposo, mientras que si es mayor, no puede ser compensada por la de rozamiento y el bloque comienza a deslizar. La frontera entre los dos casos es el estado de deslizamiento inminente.

Eso cuando se trata el bloque como una partícula. Pero en realidad, se trata de un cuerpo que tiene unas ciertas dimensiones. Entonces, al aplicar una fuerza horizontal, el bloque puede realizar un movimiento diferente: puede volcar. Es fácil ver que si el punto de aplicación de la fuerza está muy alto, el bloque puede comenzar a girar en torno a su punto de apoyo más alejado. Si el punto de aplicación, por el contrario, está a poca altura, lo más probable es que deslice.

Analicemos el problema matemáticamente. Suponemos un bloque, en forma de paralelepípedo, de anchura de la base $D$ y altura total $H$, con masa distribuida homogéneamente, de forma que su centro de masas está en su punto medio (en realidad, la forma del sólido es irrelevante, lo único que nos interesa es dónde se encuentra su centro de masas). El bloque reposa sobre un plano horizontal con el cual hay un coeficiente de rozamiento estático $\mu$. A un lado del sólido, en un punto B situado a una altura $h$ sobre el plano se aplica una fuerza horizontal ${\vec {F}}_{B}$. Se trata de ver en qué condiciones se alcanza el vuelco inminente, es decir que aunque se consiga el equilibrio, si la fuerza aplicada fuera solo un poco más intensa, el bloque volcaría.

Las fuerzas a las que está sometido el bloque son

• Su peso.

$M{\vec {g}}=-Mg{\vec {\jmath }}$

• La fuerza externa aplicada

${\vec {F}}_{B}=F_{B}{\vec {\imath }}$

• El conjunto de fuerzas de reacción entre el suelo y el bloque. Estas constituyen un sistema de infinitas fuerzas diferenciales (una por cada punto de contacto, que son infinitos). Cada una de estas fuerzas contiene tanto una componente normal como una de rozamiento horizontal

$\mathrm {d} {\vec {F}}_{R}=\mathrm {d} F_{n}{\vec {\jmath }}-\mathrm {d} F_{r}{\vec {\imath }}$

Sin embargo, no es preciso estudiar las fuerzas diferenciales o calcular sus integrales. Un sistema de fuerzas aplicado en un sólido es equivalente a dos elementos:

• Una fuerza, resultante de todas las fuerzas del sistema.
• Un momento, resultante del momento de todas las fuerzas del sistema respecto a un punto de nuestra elección.

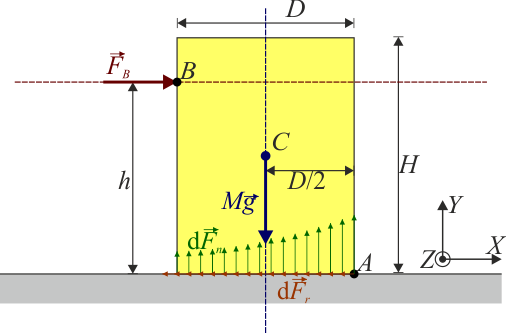
En nuestro caso, la elección natural es el posible punto alrededor del cual puede volcar el bloque. Si denominamos A a esta esquina, añadimos los elementos:

• La resultante de las fuerzas normales

${\vec {F}}_{nA}=F_{nA}{\vec {\jmath }}$

• La resultante de las fuerzas de rozamiento

${\vec {F}}_{rA}=-F_{rA}{\vec {\imath }}$

• El momento de todas las fuerzas de reacción

${\vec {M}}_{RA}=-M_{RA}{\vec {k}}$

Por el sentido de las fuerzas de reacción normales, este momento en A impide que el bloque gire en sentido positivo (antihorario), por lo que el sentido del momento aplicado debe ser negativo (horario) alrededor del eje de giro OZ.

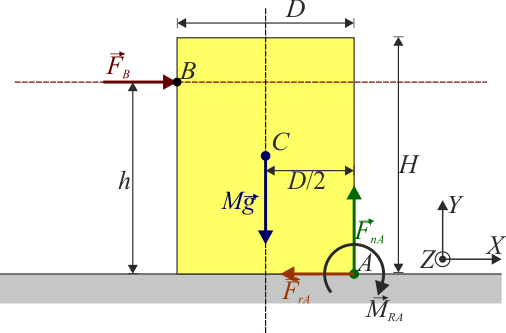
Reuniendo todo esto, y teniendo en cuenta que estamos en una situación de equilibrio, el balance de fuerzas nos da

$M{\vec {g}}+{\vec {F}}_{B}+{\vec {F}}_{nA}+{\vec {F}}_{rA}={\vec {0}}\qquad \rightarrow \qquad \left\{{\begin{array}{rcl}F_{B}-F_{rA}&=&0\\-Mg+F_{nA}&=&0\end{array}}\right.$

De estas ecuaciones obtenemos las condiciones que indicábamos antes para el deslizamiento inminente:

$F_{B}=F_{rA}\leq \mu F_{nA}=\mu Mg$

La condición de vuelco inminente la obtenemos a partir de la ecuación del momento. Hallamos el momento de todas las fuerzas respecto al punto A. Su suma debe ser nula, pues consideramos la situación de equilibrio.

${\overrightarrow {AC}}\times (M{\vec {g}})+{\overrightarrow {AB}}\times {\vec {F}}_{B}+{\vec {M}}_{RA}={\vec {0}}$

Aquí no aparecen ${\vec {F}}_{nA}$ ni ${\vec {F}}_{rA}$ porque estamos hallando el momento respecto de su propio punto de aplicación. O, dicho más correctamente, el momento de las fuerzas de contacto ya está incluido en ${\vec {M}}_{RA}$.

Cada uno de los momentos es igual, en módulo, a la intensidad de la fuerza multiplicada por el brazo del par (distancia de A a la recta soporte), con un signo dado por el sentido de giro que produce.

$\left({\frac {D}{2}}Mg-F_{B}h-M_{RA}\right){\vec {k}}={\vec {0}}$

A este mismo resultado se llega, por supuesto, sustituyendo los vectores de posición y hallando los productos vectoriales. Puesto que tenemos una sola componente podemos escribir esto en la forma escalar

${\frac {D}{2}}Mg-F_{B}h=M_{RA}\geq 0$

Por tratarse de un vínculo unilateral, el momento solo puede ir en el sentido que mencionamos antes. Por tanto, para que no haya vuelco debe cumplirse la condición

$F_{B}\leq {\frac {MgD}{2h}}$

o equivalentemente

$h\leq {\frac {MgD}{2F_{B}}}$

es decir, que la fuerza debe ser de una intensidad moderada o aplicada a baja altura para que no haya vuelco.

Esta condición no es incompatible con la del deslizamiento inminente

$F_{B}\leq \mu Mg$

Tenemos entonces cuatro casos,

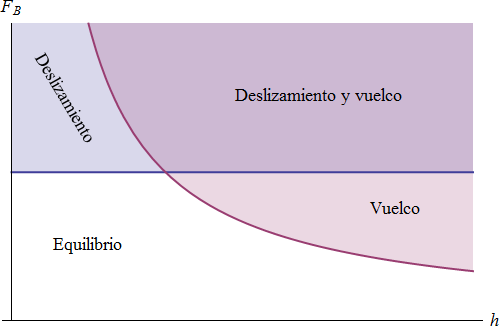
• Si la fuerza es moderada y la altura del punto de aplicación es baja, el bloque permanece en equilibrio.
• Si la fuerza es moderada, pero se aplica a gran altura, puede producirse el vuelco.
• Si la fuerza es intensa, pero aplicada a baja altura, el bloque comienza a deslizar.
• Si la fuerza es intensa y aplicada a gran altura, el bloque desliza y vuelca.

La divisoria entre las distintas regiones las dan la recta horizontal y la hipérbola

$F_{B}=\mu Mg\qquad \qquad F_{B}=\left({\frac {MgD}{2}}\right)\,{\frac {1}{h}}$

Hay que destacar que, puesto que el análisis lo hemos efectuado suponiendo condiciones de equilibrio, realmente lo único que hemos determinado es la región de color blanco en la figura, así como la forma de su frontera. Lo que ocurre fuera de esa frontera una vez que se aplica la fuerza requiere un análisis dinámico que tenga en cuenta la aceleración del centro de masas y la aceleración angular del bloque.

Sistemas análogos a este se dan en numerosas situaciones. Así tenemos el problema de si un bloque que se deja en un plano inclinado, desliza por éste o vuelca.

También se aplica un principio similar a los problemas dinámicos de la frenada o la aceleración de un vehículo, o el posible vuelco de un vehículo en una curva cerrada. En estos casos, en lugar de la fuerza aplicada, que aparece en el primer miembro del teorema de la cantidad de movimiento tenemos un término $M{\vec {a}}_{C}$ en el segundo miembro (ya que el sólido se mueve), pero el tratamiento es casi idéntico. Una demostración práctica de esto es la prueba del alce que se efectúa con los nuevos modelos de automóviles. Consiste en circular a 80 km/h por una recta y bruscamente dar un volantazo para esquivar un obstáculo y luego dar otro para retornar al carril. Se trata de evitar que el coche vuelque en el proceso, modificando la altura del CM o añadiendo otros mecanismos.

Rodadura

El caso de la rozadura sin deslizamiento es una situación frecuente de contacto entre sólidos. Cuando hay rodadura sin pivotamiento ni deslizamiento, quiere decir que, si se reduce el movimiento de uno de los sólidos respecto al otro en el punto de contacto A

${\vec {v}}_{A}={\vec {0}}\qquad \qquad {\vec {\omega }}=\omega {\vec {u}}\qquad {\vec {u}}\parallel S$

es decir, la velocidad del punto de contacto es nula y la velocidad angular es puramente tangencial a la superficie de contacto. Desde el punto de vista cinemático, el movimiento de uno de los sólidos respecto al otro es una rotación respecto a un eje instantáneo que pasa por el punto de contacto y lleva la dirección de la velocidad angular.

Ahora bien, ¿cómo se produce la rodadura desde el punto de vista dinámico? En particular, ¿cómo es que es nula la velocidad del punto de contacto?

Para que haya rodadura, debe haber fricción que impida que un sólido deslice sobre el otro. Este rozamiento es estático, no dinámico, ya que la velocidad del punto de contacto es nula. Lo producen las irregularidades del suelo. Vendría a ser lo mismo que un engranaje, pero a escala microscópica

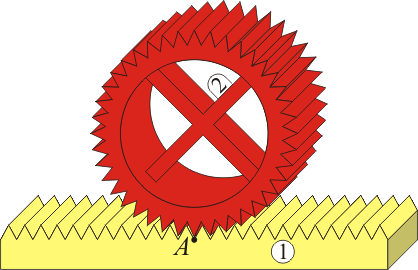
En el caso de una rueda dentada es claro que la velocidad del punto de contacto se anula. En el caso de la rodadura es lo mismo pero con “dientes” milimétricos o más pequeños. Por ello, la rodadura requiere contacto entre materiales abrasivos como goma sobre cemento, mientras que si las superficies de contacto están pulidas es más probable que se produzca deslizamiento.

El par cinemático de la rodadura impone que no haya velocidad en el punto de contacto, por lo que se anulan los tres grados de libertad de traslación, lo cual implica que en el punto de contacto se está ejerciendo una fuerza de reacción que puede tener cualquier dirección

${\vec {F}}_{R}={\vec {F}}_{n}+{\vec {F}}_{r}$

${\vec {F}}_{n}$ es la componente normal. Es una fuerza elástica debida a la impenetrabilidad de los sólidos. ${\vec {F}}_{r}$ es la fuerza de rozamiento debida a la fricción seca entre las dos superficies. Puesto que se trata de rozamiento estático, debe cumplirse

$|{\vec {F}}_{r}|\leq \mu |{\vec {F}}_{n}|$

Esto establece limitaciones sobre la posibilidad de la rodadura. Por ejemplo, si un coche al circular pisa una placa de hielo, pierde el agarre al suelo no porque empiece a levitar, sino porque μ baja bruscamente, reduciendo la fuerza de rozamiento. Ello hace que se produzca deslizamiento en el punto de contacto y el coche patina.

La fuerza de reacción en el punto de contacto es de valor desconocido a priori (al menos la componente tangencial, para la cual solo podemos dar un valor máximo). Por ello, a la hora de analizar problemas en que hay rodadura, suele ser conveniente elegir como centro de reducción el punto de contacto. De esta forma, se anula el momento de las fuerzas aplicadas en este punto y desaparecen parcialmente del problema.

La fuerza de reacción por rodadura no realiza trabajo, ya que su potencia es nula

$P={\vec {F}}_{r}\cdot {\vec {v}}_{A}=0$

Esto quiere decir que la rodadura conserva la energía mecánica. ello permite resolver problemas como el de la rodadura por una pendiente analizando la conservación de la energía.

Si además se impide el pivotamiento, existe, junto a la fuerza, un par perpendicular a la superficie de contacto que impide este giro.

Rodadura libre

Para ilustrar lo anterior consideraremos brevemente el funcionamiento de una rueda. Suponemos un sólido de sección circular caracterizado por un momento de inercia respecto a un eje que pasa por su CM,

$I=\gamma MR^{2}\,$

siendo $\gamma =1,1/2,2/3,2/5\,$ según se trate de un cilindro hueco o macizo, o una esfera hueca o maciza. También se puede generalizar sin problemas a otros sólidos circulares, como una corona cilíndrica, simplemente usando I en lugar de esta expresión particular.

Suponemos que este sólido rueda sin deslizar sobre una superficie horizontal, sometida exclusivamente a la acción de su peso y a la reacción del suelo. Nos preguntamos entonces qué fuerza lo hace girar.

La cinemática de este movimiento es la siguiente. Tomando el eje X como el de avance y el Y el vertical, con el origen de coordenadas en el centro de la rueda, el movimiento es plano, con

${\vec {v}}_{C}=v_{C}{\vec {\imath }}\qquad \qquad {\vec {\omega }}=\omega {\vec {k}}$

${\vec {k}}$ es el vector normal hacia afuera del plano, por tanto, si el giro es en sentido antihorario, $\omega$ es positiva, y si es horario negativa (regla de la mano derecha). La intuición nos dice que debe ser negativa. Esto se demuestra a partir de la condición de rodadura. Puesto que la velocidad del punto de contacto A es nula

${\vec {0}}={\vec {v}}_{A}={\vec {v}}_{C}+{\vec {\omega }}\times {\overrightarrow {CA}}=(v_{C}{\vec {\imath }})+(\omega {\vec {k}})\times (-R{\vec {\jmath }})=(v_{C}+\omega R){\vec {\imath }}$

por lo cual

$\omega =-{\frac {v_{C}}{R}}$

(nótese que se trata de una relación entre componentes, no entre vectores; la velocidad angular no es paralela a la lineal). Puesto que esta relación se cumple en todo instante, podemos derivarla respecto al tiempo y obtener una relación entre las aceleraciones

${\vec {a}}_{C}=a_{C}{\vec {\imath }}\qquad \qquad {\vec {\alpha }}=\alpha {\vec {k}}\qquad \qquad \alpha =-{\frac {a_{C}}{R}}$

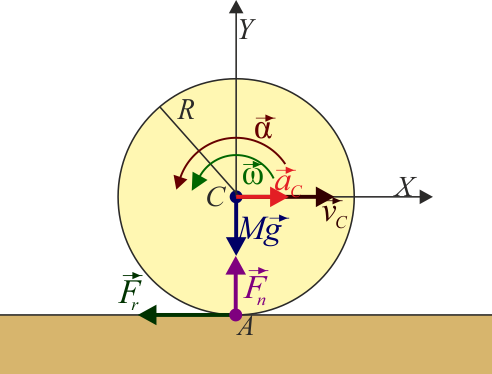
Veamos ahora la dinámica del sistema. Suponemos, de acuerdo con lo anterior, que habrá una fuerza de rozamiento estático entre el suelo y la rueda, que irá en sentido opuesto al movimiento. También imaginamos que esta fuerza de rozamiento frenará la rueda progresivamente. La ecuación para la aceleración del CM es

$M{\vec {g}}+{\vec {F}}_{n}+{\vec {F}}_{r}=M{\vec {a}}_{C}$

Separando en componentes

$-Mg{\vec {\jmath }}+F_{n}{\vec {\jmath }}-F_{r}{\vec {\imath }}=Ma_{C}{\vec {\imath }}\qquad \Rightarrow \qquad \left\{{\begin{array}{rcl}-F_{r}&=&Ma_{C}\\-Mg+F_{n}&=&0\end{array}}\right.$

con lo cual ya sabemos el valor de la fuerza normal, $F_{n}=Mg$ pero aun ignoramos el de la de rozamiento (ya que no conocemos cuánto es la aceleración del CM).

Necesitamos además la ecuación del momento de las fuerzas

$I{\vec {\alpha }}={\overrightarrow {CC}}\times (M{\vec {g}})+{\overrightarrow {CA}}\times {\vec {F}}_{n}+{\overrightarrow {CA}}\times {\vec {F}}_{r}$

De estas tres fuerzas, el peso no tiene momento, por estar aplicado en el propio CM; la fuerza normal tampoco, por estar el CM sobre la recta soporte de esta fuerza (es decir, porque ${\overrightarrow {CA}}$ y ${\vec {F}}_{n}$ son vectores paralelos); queda la fuerza de rozamiento, que si va hacia atrás produce un giro horario. Su momento es igual al valor de la fuerza multiplicada por la distancia a la recta soporte, siendo esta distancia igual al radio de la rueda. Esto da

$I\alpha =-RF_{r}\,$

Sustituyendo lo que vale $\alpha$

$F_{r}=-{\frac {I\alpha }{R}}=+{\frac {Ia_{c}}{R^{2}}}$

Tenemos entonces las ecuaciones

$F_{r}=-Ma_{c}\qquad F_{r}=+{\frac {I}{R^{2}}}a_{c}$

Según la primera de ellas, la fuerza de rozamiento frena la rueda, reduciendo la velocidad del CM; pero según la segunda, produce un giro cada vez mayor, acelerando el CM.

    

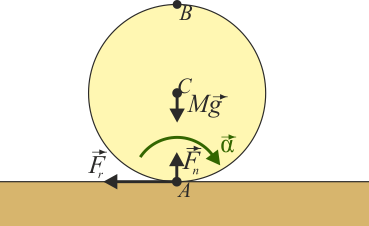
Estas dos conclusiones son contradictorias. La solución del sistema es realmente

$F_{r}=0\qquad \qquad a_{C}=0$

es decir, para una rueda que va por un plano horizontal, no hay fuerza de rozamiento y la rueda no se frena, sino que continúa moviéndose a velocidad constante.

Esto es lo que hace de la rueda una invención magistral, ya que para llevar una carga deslizando sí hay que ejercer una fuerza que venza a la de rozamiento, pero para llevarla rodando no hace falta (teóricamente; sí existe un pequeño rozamiento por rodadura debido a que los sólidos reales no son rígidos).

Rodadura con fuerza aplicada

Supongamos ahora la misma rueda del ejemplo anterior, pero sometida a una fuerza horizontal en la dirección de movimiento. Esta fuerza puede ser, por ejemplo, el empuje debido a un motor o puede ser también negativa, como sería el caso de un ciclista que experimenta la fuerza de rozamiento viscoso con el aire.

Si esta fuerza está distribuida uniformemente sobre todo el frontal, podemos sustituirla por una sola equivalente, aplicada en el CM (como ocurre con el peso, pero ahora horizontal)

${\vec {F}}_{\mathrm {apl} }=F_{\mathrm {apl} }{\vec {\imath }}$

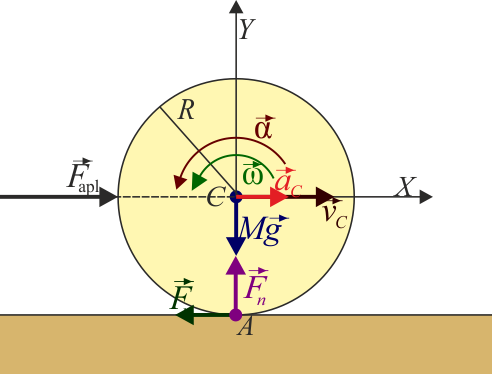
La inclusión de esta fuerza modifica las ecuaciones anteriores. Para las fuerzas

$-Mg{\vec {\jmath }}+F_{n}{\vec {\jmath }}-F_{r}{\vec {\imath }}+F_{\mathrm {apl} }{\vec {\imath }}=Ma_{C}{\vec {\imath }}\qquad \Rightarrow \qquad \left\{{\begin{array}{rcl}-F_{r}+F_{\mathrm {apl} }&=&Ma_{C}\\-Mg+F_{n}&=&0\end{array}}\right.$

y para los momentos

$I{\vec {\alpha }}={\overrightarrow {CC}}\times (M{\vec {g}})+{\overrightarrow {CA}}\times {\vec {F}}_{n}+{\overrightarrow {CA}}\times {\vec {F}}_{r}+{\overrightarrow {CC}}\times {\vec {F}}_{\mathrm {apl} }\qquad \Rightarrow \qquad I\alpha =-F_{r}{R}$

La nueva fuerza no añade momento alguno porque la consideramos aplicada en la línea que pasa por el CM. Un problema diferente sería, por ejemplo, el de un golpe a una bola de billar que se aplica por encima o debajo del CM.

Como se sigue cumpliendo la misma relación entre las aceleraciones

$\alpha =-{\frac {a_{C}}{R}}$

obtenemos

$Ma_{C}=-F_{r}+F_{\mathrm {apl} }={\frac {I\alpha }{R}}+F_{\mathrm {apl} }=-{\frac {Ia_{c}}{R^{2}}}+F_{\mathrm {apl} }$

De aquí despejamos la aceleración del CM

$\left(M+{\frac {I}{R^{2}}}\right)a_{C}=F_{\mathrm {apl} }\qquad \Rightarrow \qquad a_{C}={\frac {F_{\mathrm {apl} }}{M+I/R^{2}}}$

que para el caso de los cuatro cuerpos considerados con $I=\gamma MR^{2}$ se reduce a

$a_{C}={\frac {F_{\mathrm {apl} }}{M(1+\gamma )}}$

Puesto que $\gamma >0$, esto quiere decir que la aceleración que adquiere el CM es menor que la que tendría un bloque sin rozamiento sometido a la fuerza aplicada.

El valor de la fuerza de rozamiento estático entre la rueda y el suelo vale

$F_{r}=+{\frac {I}{R^{2}}}a_{C}={\frac {I/R^{2}}{M+I/R^{2}}}F_{\mathrm {apl} }$

En forma vectorial

${\vec {F}}_{r}=-F_{r}{\vec {\imath }}=-{\frac {I/R^{2}}{M+I/R^{2}}}{\vec {F}}_{\mathrm {apl} }$

Observemos que la fuerza, al ser de rozamiento estático, se opone a la fuerza aplicada. Por tanto, en el caso de una rueda que avanza sometida a un rozamiento con el aire, la fuerza de rozamiento con el suelo va hacia adelante, es decir, en el mismo sentido que la velocidad del centro de la rueda. Para explicar como es que en este caso el rozamiento parece favorecer el movimiento, en vez de oponerse a él, hay que recordar que en el punto contacto la velocidad es nula, por lo que la fuerza aplicada tiende a desplazar este punto en su propio sentido, y la fuerza de rozamiento a lo que se opone es a este desplazamiento del punto de contacto, no al del CM.

    

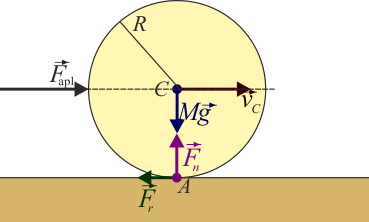
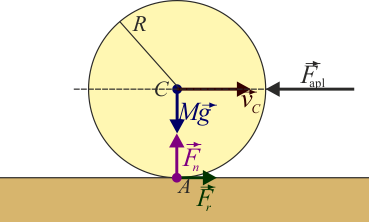
Para los cuatro cuerpos considerados

${\vec {F}}_{r}=-{\frac {\gamma }{1+\gamma }}{\vec {F}}_{\mathrm {apl} }$

En particular, para el disco, $\gamma =1/2$ y resulta una fuerza de 1/3 de la aplicada.

El límite de deslizamiento se alcanza cuando esta fuerza de rozamiento es igual, en módulo, a $\mu |{\vec {F}}_{n}|$, lo que da una cota

${\frac {I/R^{2}}{M+I/R^{2}}}F_{\mathrm {apl} }\leq \mu Mg\qquad \Rightarrow \qquad F_{\mathrm {apl} }\leq {\frac {(M+I/R^{2})\mu Mg}{I/R^{2}}}$

Una fuerza mayor que esta provoca que la rueda empiece a patinar. Esto es importante a la hora de estudiar el frenado de un vehículo, pues cuando las ruedas patinan se pierde el control de éste.

Rodadura con par aplicado

Empujar una rueda no es la única forma de que esta ruede. Consideremos el caso de la rueda trasera de una bicicleta. Esta rueda avanza porque tiene una cadena unida a ella a través de un piñón.

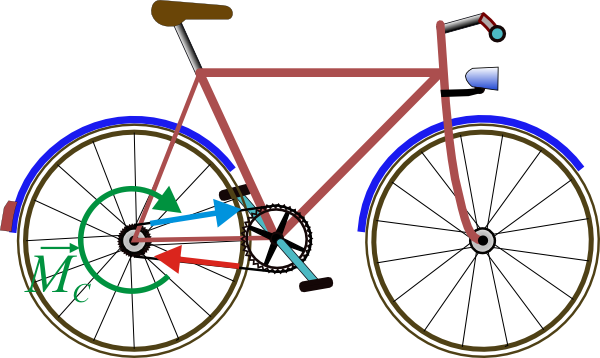
La cadena lo que hace sobre la rueda es ejercer un par de fuerzas. El tramo superior tira del piñón, mientras que el de abajo lo empuja. Si suponemos que estas dos fuerzas son paralelas e iguales en módulo $|{\vec {F}}|$ y el diámetro del piñón es $D$, el resultado es que sobre la rueda se aplica un momento en su centro

${\vec {M}}_{C}=\pm D|{\vec {F}}|{\vec {k}}$

El signo es positivo cuando el par tiende a producir un giro antihorario alrededor del eje Z y negativo en caso contrario.

Si las fuerzas son diferentes en módulo o dirección, el sistema se reduce a la aplicación de una fuerza neta, de las consideradas en el apartado anterior, y a un par como éste, siendo la solución la superposición de los dos casos por separado.

El mismo principio de la rueda de la bicicleta se puede ver más fácil en el caso de un monociclo

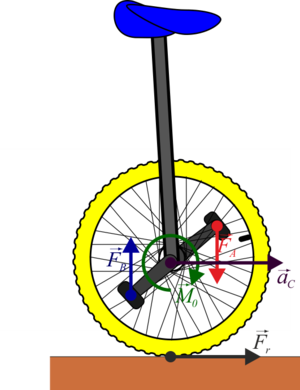
Si los pedales tienen estribos, uno de los pies ejerce una fuerza hacia abajo y el otro hacia arriba. Al ser estas fuerzas verticales no producen aceleración horizontal. Sin embargo, la rueda avanza. ¿Quién la hace avanzar?

Supongamos una rueda sometida a un par de fuerzas

${\vec {M}}_{0}=-M_{0}{\vec {k}}$

(el signo menos para que produzca un giro horario y haga avanzar la rueda hacia la derecha). Además de este par, actúan sobre ella el peso, la reacción normal y el rozamiento con el suelo horizontal. De estas fuerzas, la única horizontal es la de rozamiento. Por tanto, si la rueda avanza es porque el rozamiento la empuja. Es decir, estamos ante un caso en el que el rozamiento no se opone al movimiento, sino que es el que lo produce.

Es fácil ver por qué es así: Si no hubiera rozamiento, el par haría girar la rueda y esta patinaría sobre el suelo y en el punto de contacto se movería hacia atrás. Puesto que el rozamiento se opone el movimiento relativo, irá hacia adelante.

Si empleamos los mismos ejes que en el apartado anterior, el balance de fuerzas para esta rueda nos da las ecuaciones

$\left\{{\begin{array}{rlc}F_{r}&=&Ma_{C}\\-Mg+F_{n}&=&0\end{array}}\right.$

y el balance de momentos

$-M_{0}+F_{r}R=I\alpha =-I{\frac {a_{C}}{R}}$

Sustituyendo la fuerza de rozamiento queda

$\left(M+{\frac {I}{R^{2}}}\right)Ra_{C}=M_{0}\qquad \Rightarrow \qquad a_{C}={\frac {M_{0}R}{MR^{2}+I}}$

siendo la fuerza de rozamiento

$F_{r}=Ma_{C}={\frac {MR}{MR^{2}+I}}M_{0}$

Vemos que efectivamente esta fuerza apunta en la dirección de avance de la rueda, no en el opuesto.

Para los cuatro cuerpos circulares que estamos considerando, la aceleración y esta fuerza se reducen a

$a_{c}={\frac {M_{0}}{MR(1+\gamma )}}\qquad \qquad F_{r}={\frac {M_{0}}{R(1+\gamma )}}$

El máximo par que podemos aplicar sin que la rueda patine lo da el coeficiente de rozamiento estático

$F_{r}\leq \mu F_{n}\qquad \Rightarrow \qquad M_{0}\leq {\frac {\mu g(MR^{2}+I)}{R}}=\mu MgR(1+\gamma )$

Rozamiento por rodadura

En una situación ideal de dos sólidos perfectamente indeformables, la rodadura no disiparía ninguna energía, ya que el contacto se produciría en un solo punto, para el cual la velocidad es nula.

Sin embargo, todos los sólidos son deformables, y en el contacto de una rueda sobre el suelo éste no se produce en un solo punto, sino en una pequeña extensión (mayor cuanto más deformable sea la rueda). Dado que la rueda se encuentra en movimiento pero los puntos en contacto se hallan en reposo instantáneo, se producen esfuerzos en esos puntos, que disipan energía y producen rozamiento.

Además de la fuerza de rozamiento estático, aparece una fuerza de rozamiento por rodadura que obedece también la fórmula

$|{\vec {F}}_{r}|=\mu _{r}|{\vec {F}}_{n}|$

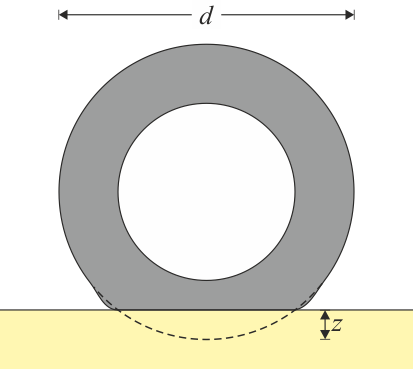
El coeficiente de rozamiento, para ruedas poco deformables, puede ser estimado como

$\mu _{r}\simeq {\sqrt {\frac {z}{d}}}$

siendo $d$ el diámetro de la rueda y $z$ la “distancia de hundimiento”. Cuanto mayor sea ésta, mayor el rozamiento. Por ello es más barato enviar mercancías por ferrocarril que por camión.

Debido al rozamiento por rodadura hay que vigilar la presión de los neumáticos:

• Si es demasiado baja, aumenta el rozamiento y se consume una cantidad excesiva de energía
• Si es demasiado alta, se hace más difícil frenar un coche, ya que se reduce el área de contacto.

Movimiento de un sólido libre

Cuando sobre un sólido la resultante de las fuerzas y el momento resultante se anulan

${\vec {F}}={\vec {0}}\qquad \qquad {\vec {M}}_{O}={\vec {0}}$

ello no implica que el sólido esté necesariamente en reposo, solo que no se ve acelerado. El estado de reposo es solo un caso particular.

En general, lo que podemos afirmar es que la cantidad de movimiento y el momento cinético permanecen constantes

${\vec {p}}=\mathrm {cte} \qquad \qquad {\vec {L}}_{O}=\mathrm {cte}$

Estas dos ecuaciones implican que también se conserva el momento cinético respecto al centro de masas

${\vec {L}}_{C}=\mathrm {cte}$

y puesto que la potencia desarrollada sobre el sólido es nula también se conserva su energía cinética

$K={\frac {1}{2}}M|{\vec {v}}_{C}|^{2}+{\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}_{C}$

De la conservación de la cantidad de movimiento se deduce que el centro de masas se mueve con un movimiento rectilíneo y uniforme.

${\vec {v}}_{C}=\mathrm {cte}$

La analogía entre traslación y rotación nos sugiere que la conservación del momento cinético implica que la velocidad angular es constante, pero esto no es cierto en general. Lo más que podemos afirmar en general es que la componente de la velocidad angular en la dirección del momento cinético sí permanece constante. Pero las componentes en otras direcciones pueden variar. El sólido puede desarrollar un movimiento de precesión en el cual el sólido gira en torno a un eje instantáneo de rotación, que está rotando a su vez.

    

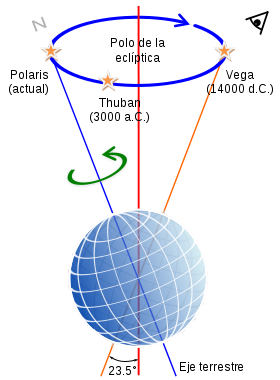
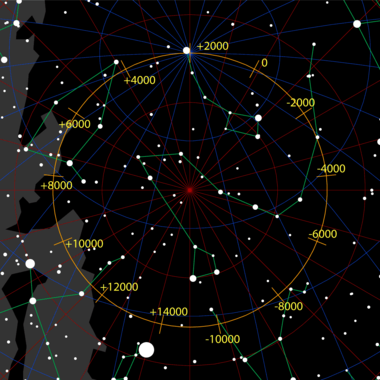
Así, por ejemplo, la Tierra es un sólido aproximadamente libre en cuanto a su rotación (no en la traslación, gobernada por la fuerza gravitatoria) y su eje desarrolla un movimiento de precesión que provoca que la estrella situada en el polo norte celeste vaya cambiando. Hoy día es la Estrella Polar, pero hace 16000 años era la estrella Vega.

En el caso de un sólido simétrico, como una esfera perfecta o un cubo, en el que la velocidad angular es paralela al momento cinético, la conservación del segundo implica la constancia de la primera

${\vec {L}}_{O}=I{\vec {\omega }}\qquad {\vec {L}}_{O}=\mathrm {cte} \qquad \Rightarrow \qquad {\vec {\omega }}=\mathrm {cte}$

Incluso en el caso de que la velocidad del CM y la velocidad angular permanezcan constantes, el movimiento de los partículas de un sólido libre puede ser muy complicado. Así, por ejemplo, en el caso de un sólido formado por dos partículas unidas por una barra, el movimiento de cada una puede ser una cicloide

Giróscopo

Un giróscopo consiste esencialmente en un sólido que, por su elevado momento de inercia y su gran velocidad de giro posee un momento cinético de gran magnitud

${\vec {L}}_{O}=I{\vec {\omega }}$

Lo que hace especial a este sólido es que un par de fuerzas aplicado sobre él apenas modifica la dirección de su eje de rotación. Por ejemplo, supongamos un disco pesado rotando alrededor del eje Z, con momento cinético respecto a su centro

${\vec {L}}_{O}=I\omega {\vec {k}}$

Supongamos que sobre este disco rotatorio se ejerce un par de fuerzas, de forma que se empuja el eje de giro a una altura $h$ por encima del disco con una fuerza $F_{0}{\vec {\imath }}$ y a una distancia $h$ por debajo una fuerza $-F_{0}{\vec {\imath }}$. ¿Hacia dónde se inclina el disco?

Un análisis ingenuo sugeriría que gira alrededor del eje OY, pero no es así. El momento del par aplicado vale

${\vec {M}}_{O}=(h{\vec {k}})\times (F_{0}{\vec {\imath }})+(-h{\vec {k}})\times (-F_{0}{\vec {\imath }})=-2hF_{0}{\vec {\jmath }}$

luego aparece una aceleración angular en la dirección del eje OY, pero esto no quiere decir que rote alrededor de este eje, ya que el disco ya poseía una cierta velocidad angular. Lo que nos da el par es la variación del momento cinético

${\frac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}={\vec {M}}_{O}\qquad \Rightarrow \qquad {\vec {L}}_{O}(t+dt)={\vec {L}}_{O}(t)+{\vec {M}}_{O}\mathrm {d} t$

En forma vectorial

${\vec {L}}_{O}(t+dt)=I\omega {\vec {k}}-2hF_{0}\,\mathrm {d} t{\vec {\jmath }}$

Esto nos da la nueva velocidad angular

${\vec {\omega }}(t+\mathrm {d} t)=\omega {\vec {k}}-{\frac {2hF\,\mathrm {d} t}{I}}{\vec {\jmath }}$

La velocidad angular es la que da el eje de giro, por lo que vemos que este eje (perpendicular al disco) adquiere una componente en la dirección del eje OY, esto es, gira en torno al eje OX (¡perpendicularmente a como diría la intuición!). Además este giro es muy pequeño, ya que el ángulo que la nueva velocidad angular forma con el eje OZ cumple

$\mathrm {tg} (\theta )={\frac {2hF\,\mathrm {d} t}{I\omega }}$

con lo cual, dado que el disco dispone de un elevado momento cinético inicial, el denominador será muy grande y el ángulo correspondiente será minúsculo. Idealmente, se supone un momento cinético infinito, con lo que es imposible variar el eje de giro. De esta forma, un giróscopo mantendría su orientación en cualquier circunstancia, sirviendo como elemento orientador, al estilo de una brújula.

Un giróscopo comercial se monta sobre un armazón consistente en una junta cardán que le permite girar manteniendo su eje siempre en la misma dirección, aunque el armazón se encuentre montado en un soporte móvil (un barco o un avión)

    

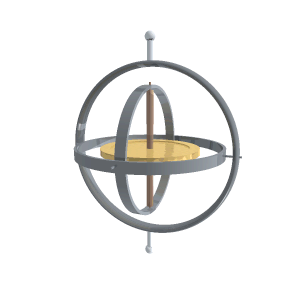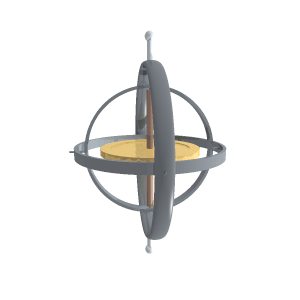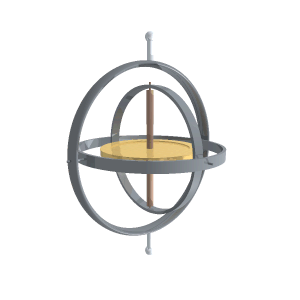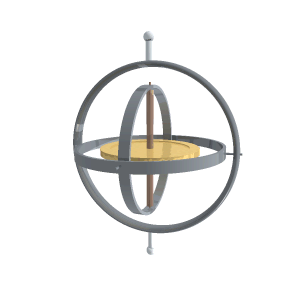
Movimiento de una peonza pesada

Una peonza sirve para describir tanto el juguete como una gran variedad de sólidos que se caracterizan por ser sólidos de revolución, tener un elevado momento de inercia alrededor del eje de simetría, y poseer un punto fijo.

El problema de la peonza pesada consiste en determinar los posibles movimientos de una peonza cuando su extremo inferior no se desplaza pero puede rotar libremente (lo que sería un par cinemático esférico), y la peonza se encuentra sometida exclusivamente a la acción de su peso.

Si la peonza no gira el comportamiento es sencillo: vuelca, cayendo como un péndulo inestable. Cuando está rotando, en cambio, el problema es mucho más complicado, ya que aparece el efecto giróscopico, que provoca que el par debido al peso cambie la dirección del eje de rotación, provocando diferentes tipos de movimientos.

El análisis matemático de este problema escapa al alcance de este resumen. Se trata de resolver unas ecuaciones diferenciales, conocidas como ecuaciones de Euler que se caracterizan por ser no lineales (esto es, si tenemos dos peonzas y la velocidad angular de la segunda es el doble de la primera, el movimiento siguiente no es el mismo que saldría simplemente multiplicando la solución de la primera por 2).

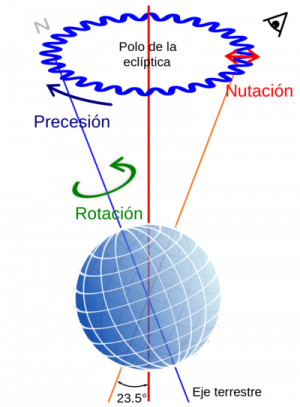
Los movimientos que puede describir la peonza son tres, que se superponen en general:

Rotación

giro alrededor del eje instantáneo de rotación.

Precesión

movimiento del propio eje de rotación, el cual gira alrededor del eje vertical marcado por la gravedad.

Nutación

balanceo del eje de rotación respecto a la vertical

Solo en casos muy precisos se consigue que la peonza simplemente rote verticalmente. En general habrá precesión y, si existen asimetrías y otras fuerzas como las de rozamiento, aparece la nutación del sólido.

La Tierra, en su movimiento alrededor del Sol, además de la rotación y la precesión mencionadas anteriormente, también presenta un movimiento de nutación, debido a la acción combinada de la atracción gravitatoria lunar y la solar.