Disco rodando sin deslizar en el interior de un camino circular
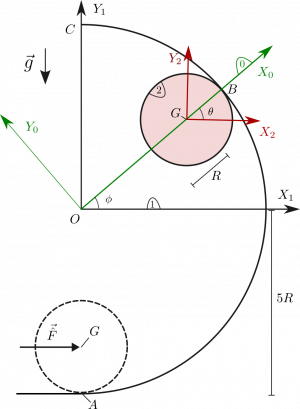
Un disco homogéneo de masa y radio (sólido "2") rueda sin deslizar sobre el interior de un arco de circunferencia de radio . Se escoge el sólido "0" de modo que el eje contiene siempre el centro del disco. La gravedad actúa como se indica en la figura. El contacto entre el disco y la superficie interior del arco de circunferencia es rugoso. Un momento de fuerzas actúa sobre el disco. Utiliza los vectores de la base "0" para expresar todos los vectores del problema.
- Escribe la reducción cinemática del movimiento {21} en el centro de masas del disco, así como su derivada temporal en función de los grados de libertad.
- Calcula la cantidad de movimiento del disco y su energía cinética.
- Usando las técnicas de Dinámica analítica, encuentra la o las ecuaciones diferenciales que describen el movimiento del disco.
- Dibuja el diagrama de fuerzas que actúan sobre el disco.
- Aplicando las técnicas de Dinámica vectorial, encuentra las ecuaciones que dan el valor de las fuerzas vinculares.
- Utilizando la técnica de los multiplicadores de Lagrange, encuentra la expresión de para que el centro del disco se mueva de modo que , con constante.
- A partir de ahora, supondremos que no hay momento aplicado. En el instante inicial el disco se encuentra al pie del arco de circunferencia (el disco a trazos de la figura), con , . Se aplica una percusión en el centro del disco. Encuentra el valor de después de la percusión.
- Si se tiene que , ¿qué valor mínimo debe tener para que el disco llegue hasta el punto sin separarse del arco de circunferencia? (El centro del disco ya no se mueve con rapidez constante)















