Enunciado

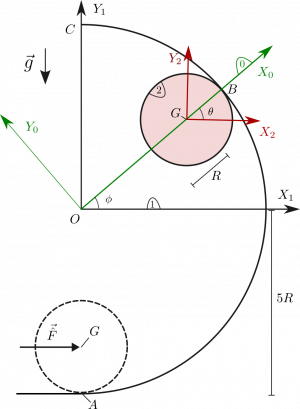
Un disco homogéneo de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m=2m_0} y radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R} (sólido "2") rueda sin deslizar sobre el interior de un arco de circunferencia de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 5R} . Se escoge el sólido "0" de modo que el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0} contiene siempre el centro Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G} del disco. La gravedad actúa como se indica en la figura. El contacto entre el disco y la superficie interior del arco de circunferencia es rugoso. Un momento de fuerzas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\tau} = \tau\,\vec{k}} actúa sobre el disco. Utiliza los vectores de la base "0" para expresar todos los vectores del problema.

  1. Escribe la reducción cinemática del movimiento {21} en el centro de masas del disco, así como su derivada temporal en función de los grados de libertad.
  2. Calcula la cantidad de movimiento del disco y su energía cinética.
  3. Usando las técnicas de Dinámica analítica, encuentra la o las ecuaciones diferenciales que describen el movimiento del disco.
  4. Dibuja el diagrama de fuerzas que actúan sobre el disco.
  5. Aplicando las técnicas de Dinámica vectorial, encuentra las ecuaciones que dan el valor de las fuerzas vinculares.
  6. Utilizando la técnica de los multiplicadores de Lagrange, encuentra la expresión de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \tau} para que el centro del disco se mueva de modo que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi}=\omega_0} , con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_0} constante.
  7. A partir de ahora, supondremos que no hay momento aplicado. En el instante inicial el disco se encuentra al pie del arco de circunferencia (el disco a trazos de la figura), con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi(0^-)=-\pi/2} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi}(0^-)=0} . Se aplica una percusión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\hat{F}}=\hat{F_0}\,\vec{\imath}_1 = \hat{F}_0\,\vec{\jmath}_0} en el centro del disco. Encuentra el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi}} después de la percusión.
  8. Si se tiene que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \hat{F}_0=12\lambda m_0\sqrt{gR}} , ¿qué valor mínimo debe tener Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda} para que el disco llegue hasta el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} sin separarse del arco de circunferencia? (El centro del disco ya no se mueve con rapidez constante)

Solución

Se trata de un movimiento plano. En este tipo de problemas, el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Z } , y por tanto el vector Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{k} } es común a todos los sólidos. Tal como están elegidos los ejes en la figura, el sentido positivo del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Z } apunta hacia fuera. El disco tiene como máximo tres grados de libertad.

Reducción cinemática

Movimiento {01}

El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O } es un punto fijo del sólido "0" ( el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0 } ) y el sólido "1" ( el camino circular). El ángulo que forma el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0 } con el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_1 } es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi } . Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{01} = \dot{\phi}\,\vec{k}, \qquad \vec{v}^{\,O}_{01} = \vec{0}. }

Podemos derivar respecto del tiempo estos vectores para obtener la derivada temporal de la reducción cinemática

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\alpha}_{01} = \left.\dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1 = \ddot{\phi}\,\vec{k}, \qquad \vec{a}^{\,O}_{01} = \left.\dfrac{\mathrm{d}\vec{v}^{\,O}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}. }

Movimiento {20}

El centro del disco Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G } es un punto fijo del sólido "2" (el disco) y el sólido "0" ( el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0 } ). Además el ángulo que forma el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_2 } con el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0 } es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta } . Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20} = -\dot{\theta}\,\vec{k}, \qquad \vec{v}^{\,G}_{20} = \vec{0}. }

El signo negativo en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20} } se razona así. Este vector rotación describe el movimiento de los ejes "2" respecto a los ejes "0", manteniendo quietos estos últimos. Si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}>0 } , el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta } aumenta. Como el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0 } es el que se mantiene fijo, el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_2 } rota hacia abajo, por lo que el vector rotación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20} } tiene que apuntar hacia dentro, para que describa correctamente la rotación.

Podemos derivar respecto del tiempo estos vectores para obtener la derivada temporal de la reducción cinemática

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0 = -\ddot{\theta}\,\vec{k}, \qquad \vec{a}^{\,G}_{20} = \left.\dfrac{\mathrm{d}\vec{v}^{\,G}_{20}}{\mathrm{d}t}\right|_0 = \vec{0}. }

Movimiento {21}

Usamos la composición de movimiento {21} = {20} + {01}. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{ll} \vec{\omega}_{21} = &\vec{\omega}_{20} + \vec{\omega}_{01} = (\dot{\phi} - \dot{\theta})\,\vec{k}.\\ \vec{v}^{\,G}_{21} = & \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01} = 4R\dot{\phi}\,\vec{\jmath}_0. \\ & \vec{v}^{\,G}_{20} = \vec{0}\\ & \vec{v}^{\,G}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OG} = 4R\dot{\phi}\,\vec{\jmath}_0.\\ & \qquad \overrightarrow{OG} = 4R\,\vec{\imath}_0. \end{array} }

Tenemos que aplicar la ligadura de rodadura sin deslizamiento. Esta ligadura implica que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\,B}_{21}=\vec{0} } . Usando la ecuación del campo de velocidades del movimiento {21} obtenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{ll} \vec{v}^{\,B}_{21} = & \vec{v}^{\,G}_{21} + \vec{\omega}_{21}\times\overrightarrow{GB} = R(5\dot{\phi} - \dot{\theta})\,\vec{\jmath}_0.\\ & \overrightarrow{GB} = R\,\vec{\imath}_0. \end{array} }

Imponiendo que esta velocidad tiene que ser cero obtenemos la ligadura

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta} = 5\dot{\phi}. }

Por tanto la reducción cinemática del movimiento {21} en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G } es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21} = -4\dot{\phi}\,\vec{k}, \qquad \vec{v}^{\,G}_{21} = 4R\dot{\phi}\,\vec{\jmath}_0. }

Vemos que hay sólo un grado de libertad. Otra forma de llegar a este resultado es observar que la ligadura de rodadura sin deslizamiento en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\,B}_{21}=\vec{0} } , prohibe dos movimientos (estamos en movimiento plano). Es decir, son dos vínculos. Como el número máximo de grados de libertad es tres, vemos que sólo hay un grado de libertad.

Aplicamos las leyes de composición para obtener la derivada temporal de la reducción cinemática

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{\alpha}_{21} = \vec{\alpha}_{20} + \vec{\alpha}_{01} + \vec{\omega}_{01}\times\vec{\omega}_{20} = -4\ddot{\phi}\,\vec{k}. \\ \vec{a}^{\,G}_{21} =\vec{a}^{\,G}_{20} + \vec{a}^{\,G}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,G}_{20} = -4R\dot{\phi}^2\,\vec{\imath}_0 + 4R\ddot{\phi}\,\vec{\jmath}_0. \\ \quad \vec{a}^{\,G}_{20}= \vec{0}. \\ \quad \vec{a}^{\,G}_{01} = \vec{a}^{\,O}_{01} + \vec{\alpha}_{01}\times\overrightarrow{OG} -|\vec{\omega}_{01}|^2\overrightarrow{OG} = -4R\dot{\phi}^2\,\vec{\imath}_0 + 4R\ddot{\phi}\,\vec{\jmath}_0.\\ \qquad \overrightarrow{OG} = 4R\,\vec{\imath}_0.\\ \quad 2\vec{\omega}_{01}\times\vec{v}^{\,G}_{20} = \vec{0}. \end{array} }

Cantidad de movimiento y energía cinética

La cantidad de movimiento del disco es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{C} = m\vec{v}^{\,G}_{21} = 8m_0R\dot{\phi}\,\vec{\jmath}_0. }

Para calcular la energía cinética, usamos que es un movimiento plano. Por tanto, no hace falta utilziar el tensor de inercia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} T = T_{tras} + T_{rot} = 24m_0R^2\dot{\phi}^2\\ \\ \quad T_{tras} = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 = 16m_0R^2\dot{\phi}^2. \\ \\ \quad T_{rot} = \dfrac{1}{2}I_G|\vec{\omega}_{21}|^2 = 8m_0R^2\dot{\phi}^2 \\ \\ \quad \quad I_G = \dfrac{1}{2}mR^2 = m_0R^2. \end{array} }

Ecuación de movimiento con Dinámica analítica

La función de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L = T - U. }

La energía cinética la tenemos del apartado anterior. La energía potencial es la que corresponde a la gravedad. Eligiendo como referencia de energía potencial gravitatoria la altura del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1} , tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U = mg4R\,\mathrm{sen}\,\phi = 8m_0gR\,\mathrm{sen}\,\phi. }

Por tanto la función de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L = 24m_0R^2\dot{\phi}^2 - 8m_0gR\,\mathrm{sen}\,\phi. }

Sólo hay un grado de libertad. Entonces sólo hay una ecuación de movimiento

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}}{\mathrm{d}t} \left( \dfrac{\partial L}{\partial \dot{\phi}} \right) - \dfrac{\partial L}{\partial \phi} = Q_{\phi}^{\,NC}. }

El término Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q_{\phi}^{\,NC} } proviene del momento de fuerza que actúa sobre el disco. Procedemos a hacer los cálculos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \dfrac{\partial L}{\partial \dot{\phi}} = 48 m_0 R^2 \dot{\phi} \Rightarrow \dfrac{\mathrm{d}}{\mathrm{d}t} \left( \dfrac{\partial L}{\partial \dot{\phi}} \right) = 48 m_0 R^2 \ddot{\phi}\\ \dfrac{\partial L}{\partial \phi} = -8m_0gR\cos\phi\\ Q^{\,NC}_{\phi} = \vec{\tau}\cdot\dfrac{\partial\vec{\omega}_{21}}{\partial\dot{\phi}} = \left(\tau\,\vec{k}\right)\cdot(-4\,\vec{k}) = -4\tau. \end{array} }

Por tanto, la ecuación de movimiento es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 12 m_0 R^2 \ddot{\phi} + 2m_0gR\cos\phi = -\tau. }

Diagrama de fuerzas

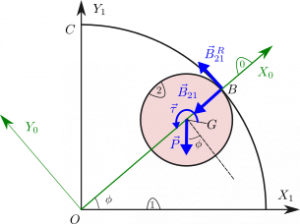
La imagen de la derecha muestra las fuerzas y momentos que actúan sobre el disco. Son las siguientes

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{ll} \vec{P} = -2m_0g\mathrm{sen}\,\phi\,\vec{\imath}_0 - 2m_0g\cos\phi\,\vec{\jmath}_0 & \mathrm{(Peso,\, aplicado\, en \, el\, punto\, G)} \\ \vec{B}_{21} = -B\,\vec{\imath}_0 & \mathrm{(Fuerza\, vincular\, normal,\, B>0,\, aplicada\, en\, el\, punto\, B)} \\ \vec{B}^{\,R}_{21} = B_R\,\vec{\jmath}_0 & \mathrm{(Fuerza\, de\, rozamiento,\, aplicada\, en\, el\, punto\, B)} \\ \vec{\tau} = \tau\,\vec{k}& \mathrm{(Momento\, aplicado)} \end{array} }

La fuerza de rozamiento puede ir en cualquiera de los dos sentidos. La fuerza vincular normal debe apuntar hacia el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O } , pues el vínculo es unilateral.

Dinámica vectorial

Las leyes que describen el movimiento del disco son el Teorema del Centro de Masas (TCM) y el Teorema del Momento Cinético (TMC).

TCM

El teorema dice que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_1 = \vec{P} + \vec{B}_{21} + \vec{B}_{21}^{\,R}. }

Como la cantidad de movimiento está expresada en la base del sólido "0", tenemos que aplicar la fórmula de Poisson para hacer la derivada temporal

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_1 = \left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_0 + \vec{\omega}_{01}\times\vec{C} = -8m_0R\dot{\phi}^2\,\vec{\imath}_0 + 8m_0R\ddot{\phi}\,\vec{\jmath}_0. }

También podemos hacer

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dfrac{\mathrm{d}\vec{C}}{\mathrm{d}t}\right|_1 = m\vec{a}^{\,G}_{21} = -8m_0R\dot{\phi}^2\,\vec{\imath}_0 + 8m_0R\ddot{\phi}\,\vec{\jmath}_0. }

Proyectando el TCM en los ejes "0" obtenemos dos ecuaciones

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lclr} X_0) & \to & 8m_0R\dot{\phi}^2 = 2m_0g\,\mathrm{sen}\,\phi + B. & (1)\\ Y_0) & \to & 8m_0R\ddot{\phi} = 2m_0g\cos\phi + B_R. & (2) \end{array} }

TMC

Aplicamos el TMC en el centro de masas del disco

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dfrac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}\right|_1 = \vec{M}_G^{\,Tot} = \overrightarrow{GB}\times\vec{B}_{21}^{\,R} + \vec{\tau}. }

El peso no crea momento respecto de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G } pues está aplicado en él. La fuerza normal tampoco pues el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G } está en su recta soporte.

El vector Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{k} } es el mismo para todos los sólidos, por lo que la derivada temporal es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dfrac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}\right|_1 = -4m_0R^2\ddot{\phi}\,\vec{k}. }

El producto vectorial es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{GB}\times\vec{B}_{21}^{\,R} = (R\,\vec{\imath}_0)\times(B_R\,\vec{\jmath}_0) = RB_R\,\vec{k}. }

La ecuación que obtenemos es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -4m_0R^2\ddot{\phi} = \tau + RB_R. \quad (3) }

Las incógnitas son Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{\phi, B, B_R\} } . Con las tres ecuaciones tenemos planteado el problema. Despejando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B_R } de (2) y sustiuyendo en (3) obtenemos la misma ecuación de movimiento del apartado 3. Una vez resuelto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi(t)} , con las correspondientes condiciones iniciales, las fuerzas vinculares se obrtendrían con las expresiones

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{B}_{21} = -4m_0\,(4R\dot{\phi}^2 - g\,\mathrm{sen}\,\phi)\,\vec{\imath}_0, \\ \vec{B}_{21}^{\,R} = 2m_0\,(4R\ddot{\phi} + g\cos\phi)\,\vec{\jmath}_0. \end{array} }

Valor del momento aplicado para que ruede con velocidad angular constante

En este caso consideramos el vínculo cinemático

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle g = \dot{\phi} - \omega_0 = 0. }

Como este vínculo afecta a una rotación, el multiplicador de Lagrange asociado es una componente de momento angular. Es decir, el multiplicador de Lagrante es la componente del momento aplicado

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu = \pm\tau. }

El signo depende de en que sentido escojamos la definición del vínculo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle g } .

La ecuación de movimiento con el multiplicador de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d}}{\mathrm{d}t} \left( \dfrac{\partial L}{\partial\dot{\phi}} \right) - \dfrac{\partial L}{\partial \phi} = Q^{\,ML}_{\phi}. }

La función de Lagrange y, por tanto, el lado izquierdo de la ecuación es el mismo que en el apartado 3. El lado derecho es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q^{\,ML}_{\phi} = \mu\dfrac{\partial g}{\partial\dot{\phi}} = \mu }

La ecuación queda

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu = 12m_0R^2\ddot{\phi} + 2m_0gR\cos\phi }

Esta ecuación es la misma que la obtenida en el apartado 3, salvo por el signo del multiplicador. Aplicando el vínculo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle g} obtenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mu = 2m_0gR\cos(\omega_0 t + \phi(0)). }

El valor Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi(0) } es el valor inicial del ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi } . El momento debe ir hacia dentro, para que el disco suba por la circunferencia. Entonces, el momento aplicado debe ser

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\tau} = -2m_0gR\cos(\omega_0 t + \phi(0))\,\vec{k}. }

Percusión

A partir de ahora no hay momento aplicado. La función de Lagrange es la misma que en el apartado 3.

En el instante en que se produce la percusión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi(0) = -\pi/2 } . Es decir, el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0} coincide con el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -Y_1} y el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_0} coincide con el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_1}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}_0(0) = -\vec{\jmath}_1, \qquad \vec{\jmath}_0 = \vec{\imath}_1. }

Por eso se da la percusión expresada en la base "0" y "1".

La ecuación de Lagrange percusiva es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta p_{\phi} = \hat{Q}_{\phi}. }

El momento generalizado es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_{\phi} = \dfrac{\partial L}{\partial\dot{\phi}} = 48m_0R^2\dot{\phi}. }

La variación del momento generalizado es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Delta p_{\phi} = 48m_0R^2\Delta(\dot{\phi}) = 48m_0R^2\dot{\phi}^+. }

La percusión generalizada es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \hat{Q}_{\phi} = \left. \vec{\hat{F}}\cdot\dfrac{\partial\vec{v}^{\,G}_{21}}{\partial\dot{\phi}} \right|_{t=0^-} = (\hat{F}_0\,\vec{\jmath}_0)\cdot(4R\,\vec{\jmath}_0) = 4R\hat{F}_0. }

De la ecuación de Lagrange percusiva obtenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi}^+ = \dfrac{\hat{F}_0}{12m_0R}. }

Condición para que el disco llegue al punto C sin separarse

En esta situación, después de la percusión aplicada sobre el centro del disco, este rueda sin deslizar subiendo por el interior de la circunferencia. Para que llege hasta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C } sin separarse tiene que ocurrir que la fuerza normal Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{B}_{21} } nunca se anule. Por tanto, la condición límite es que, en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C } , se cumpla Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle |\vec{B}_{21}| = 0 } . Es decir,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi=\pi/2 \Longrightarrow \left.B\right|_C = 0. }

Las ecuaciones obtenidas en el apartado 5 son válidas en este caso, tomando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \tau=0} . La condición entonces se expresa como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.B\right|_C = \left.B\right|_{\phi=\pi/2} = 0 \Longrightarrow \left.4m_0R\dot{\phi}^2\right|_{\phi=\pi/2} = m_0g \Longrightarrow \left.\dot{\phi}^2\right|_{\phi=\pi/2} = \left.\dot{\phi}^2\right|_C=g/4R. }

Ahora bien, dado que no hay momento externo aplicado, la energía mecánica del disco se conserva durante el movimiento. Recordemos que en una rodadura sin rozamiento la fuerza de rozamiento no hace trabajo, pues el punto de contacto entre el disco y la circunferencia, donde se aplica la fuerza de rozamiento, tiene velocidad relativa nula.

Usando los resultados del apartado 3, podemos escribir la energía mecánica en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A } y en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} E_A = \left.E\right|_{\phi=-\pi/2} = -8m_0gR + 24m_0R^2\left.\dot{\phi}^2\right|_A \\ E_C = \left.E\right|_{\phi=\pi/2} = 8m_0gR + 24m_0R^2\left.\dot{\phi}^2\right|_C \end{array} }

Igualando las energías mecánicas llegamos a

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dot{\phi}^2\right|_A = \left.\dot{\phi}^2\right|_C + \dfrac{2g}{3R}. }

De la percusión del apartado anterior tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dot{\phi}\right|_A = \dfrac{\hat{F}_0}{12m_0R} = \lambda\,\sqrt{g/R}, }

donde hemos utilizado que el enunciado dice que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \hat{F}_0 = 12\lambda m_0\sqrt{gR} } . De la condición de que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left. B\right|_C=0 } hemos obtenido el valor mínimo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\dot{\phi}\right|_C } . Sustiyendo obtenemos el valor mínimo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \lambda \geq \sqrt{\dfrac{11}{12}}. }

Obtenido de «http://laplace.us.es/wiki/index.php?title=Disco_rodando_sin_deslizar_en_el_interior_de_un_camino_circular&oldid=2750»
Obtenido de «http://laplace.us.es/wiki/index.php?title=Disco_rodando_sin_deslizar_en_el_interior_de_un_camino_circular&oldid=2750»