Masas unidas por una cuerda con muelle
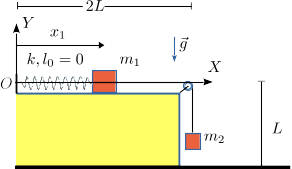
En el sistema mostrado en la figura la masa desliza sobre una superficie horizontal lisa. La masa se mueve siempre sobre una línea vertical. Se cumple . Ambas masas son tan pequeñas que pueden considerarse puntuales. El muelle tiene constante elástica y longitud natural nula. La longitud de la cuerda que une las masas es . En el instante inicial se tiene , de modo que la masa está a la misma altura que la masa . En ese instante las masas están en reposo. En un primer momento consideramos que la polea no tiene masa.
- Calcula la rapidez de la masa cuando golpea el suelo.
- Ahora consideramos que el contacto entre la masa y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico . En esta situación, calcula la rapidez con que la masa golpea el suelo
- ¿Qué condición debe cumplir para que la masa no llegue a impactar con el suelo?
- Supongamos ahora que la polea es un aro de masa y radio . El momento de inercia respecto un eje que pase por su centro es . Consideramos de nuevo la situación sin rozamiento. Calcula en este caso, la rapidez de la masa cuando golpea el suelo.









