Segunda Convocatoria Ordinaria 2016/17 (MR G.I.C.)

Disco sobre barra en forma de L

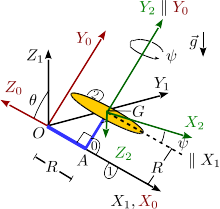
El disco homogéneo de la figura (sólido "2") tiene masa $m$ y radio $R$. Está conectado por su centro $G$ con una estructura (sólido "0") formada por dos barras perpendiculares de masas despreciables y longitud $R$ cada una. El disco puede rotar alrededor del eje $AG$, mientras que el sólido "0" puede rotar respecto a la línea $OA$. Se escoge unos ejes intermedios $OX_{0}Y_{0}Z_{0}$ de modo que el plano $OX_{0}Y_{0}$ contiene siempre al sólido "0" y al centro del disco $G$. Los ejes $GX_{2}Y_{2}Z_{2}$ son solidarios con el disco. El eje $GY_{2}$ es paralelo al eje $OY_{0}$, por lo que el plano $GX_{2}Z_{2}$ es siempre paralelo al plano $OX_{0}Z_{0}$ y el eje $GX_{2}$ forma un ángulo $\psi$ con la dirección del eje $X_{1}$. El sistema está sometido a la acción de la gravedad con la dirección y sentido indicada en la figura.

1. Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21} en el centro de masas del disco, así como la derivada temporal del {21}. Determina el eje instantáneo de rotación del movimiento {21}.
2. Calcula el momento cinético del disco respecto a $G$, su energía cinética y su energía potencial.
3. Encuentra las integrales primeras del movimiento que puedas, justificando porqué lo son.
4. Supongamos a partir de ahora que $\theta =\pi /2$ en todo instante.¿Como es la reducción cinemática {21} en $G$ y su derivada temporal?
5. En este último caso, calcula la desvinculación global {21} en G. Aplicando los teoremas fundamentales, encuentra la ecuación de movimiento para el grado de libertad restante.

Deslizadera y disco rodando sin deslizar

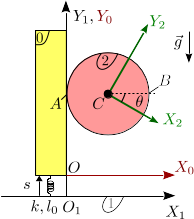
Un disco homogéneo (sólido "2") de masa $m$ y radio $R$ puede rotar alrededor de su centro $C$, que se mantiene fijo. Una deslizadera vertical (sólido "0"), de masa $m$ puede moverse a lo largo del eje $O_{1}Y_{1}$, de modo que en el punto de contacto $A$ el disco rueda sin deslizar sobre el sólido "0". La deslizadera está conectada a un muelle de constante elástica $k$ y longitud natural $l_{0}$. El otro extremo del muelle está anclado en un punto fijo del eje $O_{1}X_{1}$, de modo que se mantiene siempre vertical. El sistema está sometido a la acción de la gravedad como se indica en la figura.

1. ¿Cuantos grados de libertad tiene el sistema? Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas temporales. El resultado debe quedar en función del número de grados de libertad y sus derivadas temporales.
2. Calcula las energías cinética y potencial del sistema en función de sus grados de libertad.
3. Escribe la lagrangiana del sistema, así como las ecuaciones diferenciales de movimiento.
4. Se aplica sobre el disco un par de fuerzas externo ${\vec {\tau }}=\tau _{0}\cos(\omega t)\,{\vec {k}}_{1}$. Encuentra las ecuaciones de movimiento en este caso. ¿Para qué valor de $\omega$ aparece una resonancia mecánica?
5. Ahora no hay par aplicado. Se aplica una percusión ${\vec {\hat {F}}}=[{\hat {F}}_{0},{\hat {F}}_{0},0]_{1}$ sobre el punto $B$ del sólido "2". En el instante de la percusión se cumple $s(0)=l_{0}$, $\theta (0)=0$, ${\dot {s}}(0^{-})=0$, ${\dot {\theta }}(0^{-})=0$. Calcula el estado del sistema inmediatamente después de la percusión.