Segunda Convocatoria Ordinaria 2013/14 (G.I.C.)

Partícula en barra giratoria con dos muelles

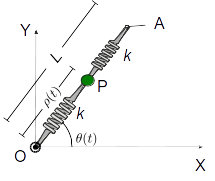
Una partícula $P$ de masa $m$ desliza sin rozamiento a lo largo de una varilla $OA$ de longitud $L$. Actúan sobre ella dos muelles, ambos de longitud natural nula y constante elástica $k$, anclados en los puntos $O$ y $A$, respectivamente. El efecto de la gravedad es despreciable.

1. Escribe las expresiones del vector posición y velocidad de la partícula en coordenadas cartesianas y polares. Deja las expresiones en función de $r(t)$, $\theta (t)$ y sus derivadas temporales.
2. Dibuja el diagrama de cuerpo libre de la partícula y escribe, usando coordenadas polares, las dos componentes de la Segunda Ley de Newton aplicada al movimiento de la partícula.
3. Supongamos que la barra gira con velocidad angular constante $\omega$. Durante el giro, la distancia de la partícula al origen permanece constante. ¿Cuánto vale esa distancia? ¿Que condición debe cumplirse para que esta situación sea posible físicamente?
4. Calcula el valor numérico de los módulos de todas las fuerzas que actúan sobre la partícula en la situación del apartado anterior y con estos valores numéricos: $m=10.0\,\mathrm {g}$, $k=100\,\mathrm {N/m}$, $L=100\,\mathrm {cm}$, $\omega =5.00\,\mathrm {rad/s}$.

Polea con masa colgando y freno

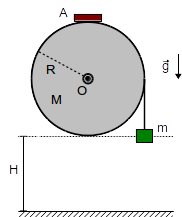
El disco de la figura, de radio $R$ y masa $M$, puede rotar sin rozamiento alrededor de un eje perpendicular al plano del papel y que pasa por $O$. La masa $m$ cuelga de una cuerda vertical, inextensible y sin masa, de modo que su altura respecto del suelo $H$ coincide con la del borde inferior del disco. En el punto $A$, un freno ejerce una fuerza de rozamiento sobre el disco de módulo $F_{R}$. Todo el sistema está sometido a la fuerza de la gravedad con la dirección que se indica en la figura. El momento de inercia de un disco respecto a un eje perpendicular a él que pasa por su centro es $I=MR^{2}/2$.

1. Dibuja el diagrama de cuerpo libre del disco y de la masa, cuando el sistema está en equilibrio estático.
2. ¿Cuánto valen los módulos de todas las fuerzas que actúan sobre el disco en situación de equilibrio estático?
3. Liberamos el freno y la masa $m$ cae con velocidad siempre vertical. Calcula la aceleración angular del disco.
4. Calcula el módulo de la velocidad de la masa cuando impacta en el suelo y la velocidad angular de rotación del disco en ese instante.