Polea con masa colgando y freno, Septiembre 2014 (G.I.C.)

Enunciado

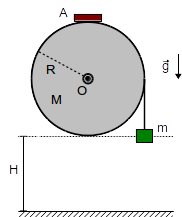
El disco de la figura, de radio $R$ y masa $M$, puede rotar sin rozamiento alrededor de un eje perpendicular al plano del papel y que pasa por $O$. La masa $m$ cuelga de una cuerda vertical, inextensible y sin masa, de modo que su altura respecto del suelo $H$ coincide con la del borde inferior del disco. En el punto $A$, un freno ejerce una fuerza de rozamiento sobre el disco de módulo $F_{R}$. Todo el sistema está sometido a la fuerza de la gravedad con la dirección que se indica en la figura. El momento de inercia de un disco respecto a un eje perpendicular a él que pasa por su centro es $I=MR^{2}/2$.

1. Dibuja el diagrama de cuerpo libre del disco y de la masa, cuando el sistema está en equilibrio estático.
2. ¿Cuánto valen los módulos de todas las fuerzas que actúan sobre el disco en situación de equilibrio estático?
3. Liberamos el freno y la masa $m$ cae con velocidad siempre vertical. Calcula la aceleración angular del disco.
4. Calcula el módulo de la velocidad de la masa cuando impacta en el suelo y la velocidad angular de rotación del disco en ese instante.

Solución

Diagramas de cuerpo libre y fuerzas

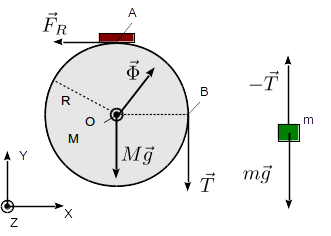
La figura muestra las fuerzas que actúan sobre la polea y la masa y los puntos donde se aplican. Las fuerzas que actúan sobre la polea son: su peso, aplicado en $O$; la fuerza que ejerce la cuerda, aplicada en $B$; la que ejerce el freno, tangente a la polea y aplicada en $A$; y la fuerza de reacción vincular del eje sobre la polea, aplicada en $O$. Usando los ejes indicados en la figura estas fuerzas se expresan como

${\begin{array}{l}M{\vec {g}}=-Mg\,{\vec {\jmath }}\\\\{\vec {T}}=-T\,{\vec {\jmath }}\\\\{\vec {F}}_{R}=-F_{R}\,{\vec {\imath }}\\\\{\vec {\Phi }}=\Phi _{x}\,{\vec {\imath }}+\Phi _{y}\,{\vec {\jmath }}\end{array}}$

La fuerza de reacción vincular en $O$ tiene a priori componentes en las tres direcciones del espacio. Como en este problema todas las fuerzas con coplanarias con el plano $OXY$ ignoramos la componente en el eje $OZ$. Pero si sabemos que, en condiciones de equilibrio estático no puede ser vertical, pues tiene que ser capaz de contrarrestar la fuerza que ejerce el freno, que es puramente horizontal.

La masa que cuelga es puntual, y esta sometida a su peso y a la fuerza de la cuerda. Como ésta no tiene masa, la fuerza que la cuerda ejerce sobre la masa es igual a la que ejerce sobre la polea con signo cambiado. Las fuerzas sobre la masa se expresan como

${\begin{array}{l}m{\vec {g}}=-mg\,{\vec {\jmath }}\\\\-{\vec {T}}=-T\,{\vec {\jmath }}\end{array}}$

Módulos de las fuerzas en situación de equilibrio estático

Aplicamos las condiciones de equilibrio estático a la masa y a la polea por separado. Como la masa es puntual, la única condición que se aplica es que la suma de fuerzas que actúan sobre ella sea cero

$m{\vec {g}}-{\vec {T}}={\vec {0}}\Longrightarrow {\vec {T}}=m{\vec {g}}$

La polea es un sólido rígido, por lo que las condiciones de equilibrio es que se anulen tanto la suma de fuerzas como de momentos que actúan sobre ella. De la suma de fuerzas obtenemos

$M{\vec {g}}-{\vec {T}}+{\vec {F}}_{R}+{\vec {\Phi }}={\vec {0}}\Longrightarrow \left\{{\begin{array}{ll}(X):\qquad \Phi _{x}-F_{R}=0&\to \Phi _{x}=F_{R}\\\\(Y):\qquad \Phi _{y}-Mg-mg=0&\to \Phi _{y}=(M+m)g\end{array}}\right.$

Escogemos el punto $O$ para calcular los momentos. Con esta elección, las únicas fuerzas con momento no nulo son las aplicadas en $A$ y en $B$. Tenemos

${\begin{array}{l}{\overrightarrow {OA}}\times {\vec {F}}_{R}=\left(R\,{\vec {\jmath }}\right)\times \left(-F_{R}\,{\vec {\imath }}\right)=RF_{R}\,{\vec {k}}\\\\{\overrightarrow {OB}}\times (-{\vec {T}})=\left(R\,{\vec {\imath }}\right)\times \left(-mg\,{\vec {\jmath }}\right)=-Rmg\,{\vec {k}}\\\end{array}}$

La suma debe ser cero, de donde obtenemos

$F_{R}=mg$

Con esto podemos expresar todas las fuerzas que actúan sobre el disco y sus módulos

${\begin{array}{ll}M{\vec {g}}=-Mg\,{\vec {\jmath }}&\to |M{\vec {g}}|=Mg\\\\{\vec {T}}=-mg\,{\vec {\jmath }}&\to |{\vec {T}}|=mg\\\\{\vec {F}}_{R}=-mg\,{\vec {\imath }}&\to |{\vec {F}}_{R}|=Mg\\\\{\vec {\Phi }}=mg\,{\vec {\imath }}+(M+m)g\,{\vec {\jmath }}&\to |{\vec {\Phi }}|=(M+m)g\end{array}}$

Movimiento de giro del disco

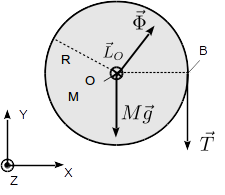
Al quitar el freno, la fuerza de rozamiento en $A$ deja de actuar. Entonces no hay ninguna fuerza capaz de contrarrestar el momento que ejerce la tensión de la cuerda respecto de $O$. La situación estática no puede mantenerse y el disco empieza a girar alrededor de un eje perpendicular a él y que pasa por $O$. El movimiento viene descrito por la variación en el tiempo del momento cinético del disco

${\dfrac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}={\vec {M}}_{O}^{total}$

Cuando la rotación se produce alrededor de un eje fijo el momento angular es

${\vec {L}}_{O}=I{\vec {\omega }}$

Aquí, $I$ es el momento de inercia del disco y ${\vec {\omega }}$ es la velocidad de rotación. El momento de inercia no cambia en el tiempo, por lo que tenemos

${\dfrac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}=I{\dot {\vec {\omega }}}=I{\vec {\alpha }}$

donde ${\vec {\alpha }}$ es la aceleración angular.

El momento es el creado por la tensión de la cuerda

${\vec {M}}_{O}^{total}={\overrightarrow {OB}}\times {\vec {T}}=-mgR\,{\vec {k}}$

Así pues la ecuación que describe el movimiento es

$I{\vec {\alpha }}=-mgR\,{\vec {k}}\Longrightarrow {\vec {\alpha }}=-{\dfrac {mgR}{I}}\,{\vec {k}}$

El disco gira con una aceleración angular constante.

Velocidad de la masa cuando impacta contra el suelo

Este apartado puede hacerse de varias formas. Vamos a usar la conservación de energía mecánica. Una vez que el disco gira, las únicas fuerzas que realizan trabajo son conservativas. Así pues se conserva la energía mecánica. Escogemos como origen de energía potencial gravitatoria el suelo. En el instante inicial la energía cinética es cero, por lo que la energía mecánica es igual a la suma de las energías potenciales de la masa y el disco

$E_{m}^{i}=mgH+Mg(H+R)$

Cuando la masa impacta contra el suelo su energía potencial es cero y tiene energía cinética. También el disco tiene energía cinética, pues está girando, mientras que su energía potencial es la misma que al principio, pues su centro no se ha movido

$E_{m}^{f}={\dfrac {1}{2}}mv_{f}^{2}+Mg(H+R)+{\dfrac {1}{2}}I\omega _{f}^{2}$

Nos falta relacionar la velocidad de la masa con la velocidad angular del disco. El punto del disco mas a la derecha tiene en cada instante la misma velocidad que la masa. Tenemos entonces

$v_{f}^{B}=v_{f}=\omega _{f}R$

Igualando las energías mecánicas inicial y final tenemos

$v_{f}={\sqrt {\dfrac {2mgH}{m+{\dfrac {I}{R^{2}}}}}}$

El enunciado nos da el momento de inercia de disco aplicable en este caso. Sustituyendo tenemos

$v_{f}={\sqrt {\dfrac {4mgH}{2m+M}}}$

Podemos comprobar que el resultado es razonable imaginando una situación en que la masa del disco fuese muy pequeña. Si hacemos el límite $M\to 0$, la velocidad final de la masa sería ${\sqrt {2gH}}$. Esta es la velocidad de un móvil que cae libremente en campo gravitatorio partiendo del reposo desde una altura $H$. También podemos ver que si la polea es muy pesada, $M\to \infty$, la velocidad de la masa tiende a cero. Esto también es razonable. En este caso la inercia del disco es tan grande que apenas gira.