Problemas de campos magnéticos (GIOI)
Secciones
Espira parcialmente inmersa en un campo magnético
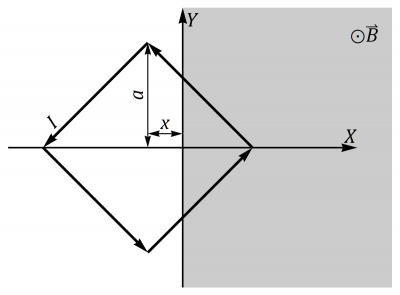
![]() El campo entre los polos de un imán se puede modelar como un campo magnético uniforme en el semiespacio . Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que su centro se halla en (x puede ser tanto negativo como positivo). Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira, así como la fuerza neta (distínga los casos necesarios en x).
El campo entre los polos de un imán se puede modelar como un campo magnético uniforme en el semiespacio . Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que su centro se halla en (x puede ser tanto negativo como positivo). Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira, así como la fuerza neta (distínga los casos necesarios en x).
Espira girada dentro de un campo magnético
![]() Una espira rectangular ABCD se encuentra en el interior de un campo magnético uniforme . Los vértices de la espira se encuentran en
Una espira rectangular ABCD se encuentra en el interior de un campo magnético uniforme . Los vértices de la espira se encuentran en
(distancias medidas en cm). Por la espira circula una corriente de 0.2 A en el sentido ABCD.
- Halle la fuerza magnética sobre cada lado de la espira, así como la fuerza total sobre la espira
- Considerando cada fuerza aplicada sobre el centro del lado correspondiente, halle el momento resultante, según la ley
- Calcule el momento magnético de la espira y compruebe que
Campo magnético producido por un segmento
Halle el campo magnético producido por un segmento rectilíneo, por el cual circula una intensidad de corriente , en cualquier punto del espacio. Para fijar ideas, sitúese el punto de medición del campo en y el segmento sobre el eje OZ extendiéndose desde a (con la corriente de A a B). Posteriormente generalícese el resultado, con ayuda de las coordenadas cilíndricas.
Campo creado por un hilo infinitamente largo
A partir del resultado del problema “Campo magnético producido por un segmento” calcule, para todos los puntos del espacio, el campo magnético creado por un hilo rectilíneo infinitamente largo situado sobre el eje OZ y por el cual circula una intensidad de corriente en el sentido del eje OZ positivo.
Campo de dos hilos paralelos
Dos hilos paralelos se hallan situados paralelamente al eje OZ, situados sobre , .
- Determine el valor del campo magnético en todos los puntos del plano , y en todos los puntos del plano en los dos casos siguientes:
- Por los hilos circulan corrientes paralelas .
- Por los hilos circulan corrientes antiparalelas .
- Para el caso particular , , ¿cuánto vale el campo magnético en el origen de coordenadas para los dos casos anteriores?
- ¿Cuánto vale la fuerza magnética que uno de los hilos ejerce sobre una porción de longitud del otro?
Campo de una espira rectangular
A partir del resultado del problema “Campo magnético producido por un segmento”, halle el campo magnético en el centro de una espira rectangular de lados y por la cual circula una intensidad de corriente .
Campo magnético de una espira circular
Halle, por integración directa, el campo magnético en los puntos del eje de una espira circular de radio , por la cual circula una intensidad de corriente . ¿Cuánto vale aproximadamente este campo en puntos alejados ()?
Campo magnético de una bobina cilíndrica
A partir del resultado del problema “Campo magnético de una espira circular” calcule el campo en los puntos del eje de una bobina cilíndrica de radio y longitud , con un número grande de vueltas, . ¿A qué se reduce este resultado en el límite en que ?

























