Primera Convocatoria Ordinaria 2015/16 (MR G.I.C.)

Aro colgando de una barra que rota

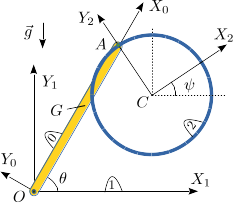
La barra homogénea $OA$ (sólido "0") tiene masa $m$ y longitud $L$. Está articulada en el punto fijo $O$ y rota de modo que está siempre contenida en el plano $OX_{1}Y_{1}$. En su extremo $A$ está articulado un aro homogéneo de radio $R$ y masa $m$ (sólido "2"). El sistema está sometido a la acción de la gravedad. Se recomienda utilizar los ángulos $\{\theta ,\psi \}$ como coordenadas para resolver el problema.

1. Determina las reducciones cinemáticas de los movimientos {01}, {21}, {20}.
2. Calcula las energías cinética y potencial totales del sistema.
3. Usando las herramientas de la Dinámica Analítica, encuentra las ecuaciones de movimiento.
4. Se impone el vínculo cinemático ${\dot {\theta }}=\omega _{0}$. Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene $\theta (0)=0$, $\psi (0)=0$.
5. Supongamos que las coordenadas $\{\theta ,\psi \}$ son de nuevo libres. Supón que se tiene $\theta (0)=0$, $\psi (0)=0$. En ese instante una percusión ${\vec {\hat {F}}}=[{\hat {F}}_{0},{\hat {F}}_{0},0]_{1}$ actúa sobre el punto $A$. Determina el estado cinemático del sistema justo después de la percusión.

Barra articulada sobre muelle

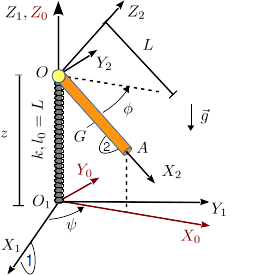
En el sistema de la figura, la barra delgada homogénea $OA$ (sólido "2"), de masa $m$ y longitud $L$, está articulada en el punto $O$. El punto $O$ puede moverse sobre el eje fijo $O_{1}Z_{1}$, y está conectado a un muelle de constante elástica $k$ y longitud natural $L$. El muelle siempre permanece vertical. La barra "2" está siempre contenida en el plano $O_{1}X_{0}Z_{0}$, como se indica en la figura.

1. Encuentra la reducción cinemática del movimiento {21} en los puntos $O$ y $G$.
2. Calcula el momento cinético de la barra "2" en $O$ y $G$ (${\vec {L}}_{O}$, ${\vec {L}}_{G}$).
3. Calcula la energía cinética de la barra "2".
4. Aplicando el T.C.M. y el T.M.C. escribe las ecuaciones de movimiento del sistema.
5. Escribe todas las integrales primeras del movimiento que puedas encontrar.