Colisión involucrando a tres partículas

Se tienen dos partículas de masa (2 y 3) en reposo separadas por una cierta distancia. Otra partícula (1) de masa se aproxima a una de ellas moviéndose sobre la recta que las une. La partícula 1 colisiona con la 2. Después de esta colisión, las partículas se mueven y se produce otra colisión con la partícula 3. Calcula la energía final de cada una de las tres partículas y la proporción de energía cinética inicial que se transmite a la partícula 3 en cada una de estas situaciones:
- Todas las colisiones son elásticas.
- La primera colisión es completamente inelástica y la segunda elástica.
Barras articuladas
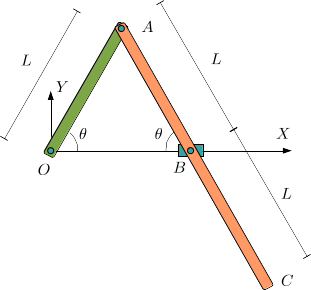
La barra tiene longitud y esta articulada en el punto . La barra está articulada en y tiene longitud . Además tiene un pasador en su punto medio , de modo que esté punto está siempre sobre el eje . La barra gira de modo que el ángulo es una función del tiempo.
- Determina los vectores de posición de los puntos , ,
- Si el punto se mueve con velocidad uniforme , determina la función si .
- Supón ahora que el ángulo varía como , con constante. En estas condiciones, calcula la velocidad y aceleración del punto , así como su aceleración tangencial.
Bloque sobre plano inclinado con cuerda
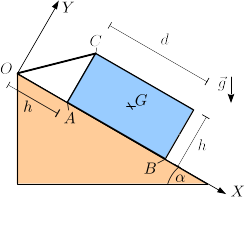
Un bloque rectangular (sólido "2") de masa , de lados y reposa sobre un plano inclinado (sólido "1") un ángulo sobre la horizontal. El vértice del bloque está unido por una cuerda con el punto . El contacto entre el bloque y el plano es liso. La distancia entre los puntos y es .
- Dibuja el diagrama de cuerpo libre del bloque.
- ¿Cuánto valen las fuerzas sobre el bloque en situación de equilibrio mecánico?
- Analiza el equilibrio frente a vuelco en función del ángulo .
- ¿Qué ocurre si añadimos rozamiento en el contacto entre el bloque y el plano?
Masa conectada a dos muelles
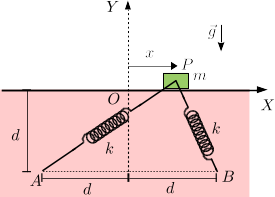
Una masa desliza sobre una superficie horizontal lisa. Está conectada a dos muelles de constante elástica y longitud natural nula anclados como se indica en la figura en los puntos y . En el instante inicial la masa está en reposo y con . }
- Dibuja el diagrama de cuerpo libre de la masa.
- Encuentra la ecuación de movimiento del bloque.
- Determina la posición del bloque y su velocidad en cada instante.
- Calcula la energía mecánica del bloque y su momento cinético respecto de para todo instante de tiempo.



















