Diferencia entre las páginas «Movimiento de barra en un pasador» y «Barra apoyada en placa»
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
[[Archivo:barra- | [[Archivo:barra-apoyada-caja.png|right]] | ||
El esquema de la figura muestra una placa cuadrada de lado <math>a</math> (sólido ``0"), uno de cuyos lados desliza sobre el eje horizontal fijo <math>OX_1</math> (sólido “1”), mientras que la placa permanece contenida siempre en el plano vertical fijo <math>OX_1Y_1</math>. Sobre el vértice A de dicha placa se apoya en todo instante una varilla delgada (sólido “2”), que gira con velocidad angular constante <math>\vec{\omega}_{21}=\Omega \vec{k}_1</math>, alrededor de su extremo articulado en el punto fijo O (ver figura). Se pide: | |||
# Determinar gráficamente la posición | # Determinar gráficamente la posición de los centros instantáneos de rotación <math>I_{21}</math>, <math>I_{02}</math> e <math>I_{01}</math>. | ||
# Calcular: i) La velocidad del vértice A de la placa en el movimiento de ésta respecto de los ejes fijos (movimiento {01}), expresada en función de la posición del sistema: <math>\vec{v}_{\! 01}^A=\vec{v}_{01}^A(\theta)</math>. ii) La velocidad angular <math>\vec{\omega}_{02}</math>, correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {02}). | |||
# Determinar analíticamente la posición del | # Determinar analíticamente la posición del CIR del movimiento {02} (en función del ángulo <math>\theta</math>). | ||
== | ==Centros instantáneos de rotación== | ||
[[Archivo:barra-placa-03.png|right]] | |||
;Del movimiento {01}: La placa realiza un movimiento de traslación horizontal, por lo que el centro instantáneo de rotación del movimiento {01} será un punto del infinito situado según la dirección vertical. | |||
;Del movimiento {21}: La barra efectúa un movimiento de rotación en torno al punto en el cual se encuentra articulada. Este punto será el CIR <math>I_{21}</math>, que de hecho en este caso se trata de un centro permanente y no solo instantáneo. | |||
;Del movimiento {20}: Por el teorema de los tres centros, el CIR <math>I_{20}</math> (coincidente con el CIR <math>I_{02}</math>) estará alineado con los otros dos. Puesto que <math>I_{01}</math> está en el infinito según la dirección vertical, el CIR <math>I_{20}</math> debe encontrarse en la vertical del punto <math>O = I_{21}</math>, esto es, se trata de un punto del eje <math>OY_1</math>. | |||
:Queda por determinar la posición sobre este eje. Para ello necesitamos la dirección de la velocidad de algún punto en el movimiento {20} o el {02}. El más simple es el punto A, donde contactan la barra y la placa. Este contacto impone un vínculo sobre las posibles velocidades de A. En particular, impide que A, en el movimiento {02}, tenga una componente perpendicular a la propia barra, ya que de ser así atravesaría ésta. | |||
:Por tanto, <math>\vec{v}^A_{20}</math> es tangente a la propia barra. Ello implica que <math>I_{20}</math> se encuentra en la intersección de la perpendicular a la barra por A con el eje <math>OY_1</math>. | |||
:Podemos obtener las coordenadas de este punto empleando trigonometría. Si la altura de la placa es <math>a</math>, la distancia OA es la hipotenusa de un triángulo rectángulo, por lo que | |||
<center><math>\ | <center><math>L = \left|\overrightarrow{OA}\right| = \frac{a}{\mathrm{sen}(\theta)}</math></center> | ||
:La altura <math>h</math> es la hipotenusa de otro triángulo rectángulo, uno de cuyos catetos es OA. Por ello | |||
<center><math>h = \frac{L}{\cos\left(\frac{\pi}{2}-\theta\right)} = \frac{a}{\mathrm{sen}^2(\theta)}</math></center> | |||
:En forma vectorial | |||
<center><math> | <center><math>\overrightarrow{OI}_{20}=\frac{a}{\mathrm{sen}^2(\theta)}\vec{\jmath}_1</math></center> | ||
A | ==Velocidades== | ||
===Conociendo la posición del CIR {20}=== | |||
Para hallar la velocidad de traslación de A (que es la misma de cualquier otro punto de la placa), podemos usar la ley de composición de velocidades | |||
<center><math> | <center><math>\vec{v}^A_{01} = \vec{v}^A_{02}+\vec{v}^A_{21}</math></center> | ||
Cada una de estas velocidades es una rotación alrededor de su correspondiente CIR | |||
<center><math>\ | <center><math>\vec{v}^A_{01} = \omega_{02}\vec{k}\times\overrightarrow{I_{02}A}+\omega_{21}\vec{k}\times\overrightarrow{I_{21}A}</math></center> | ||
La velocidad angular <math>\omega_{21}</math> la da la derivada temporal del ángulo que forma el <math>OX_1</math> con el <math>OX_2</math>, que suponemos ligado a la propia barra: | |||
<center><math>\ | <center><math>\omega_{21}=\dot{\theta}=\Omega</math></center> | ||
donde se ha tenido en cuenta que, según el enunciado del ejercicio, <math>\vec{\omega}_{21}=\Omega \vec{k}_1</math>. | |||
La del movimiento {02} la obtenemos por composición de velocidades angulares, teniendo en cuenta que el movimiento {01} es una traslación | |||
<center><math>\ | <center><math>0 = \omega_{01} = \omega_{02}+\omega_{21}\qquad\Rightarrow\qquad \omega_{02}= -\omega_{21} = -\Omega\qquad\Rightarrow\qquad \vec{\omega}_{02}=-\Omega \vec{k}_1</math></center> | ||
y | Resulta una velocidad angular igual y opuesta a la primera. De aquí llegamos a la velocidad de traslación | ||
<center><math>\ | <center><math>\vec{v}^A_{01} = \Omega\left(-\vec{k}\times\overrightarrow{I_{02}A}+\vec{k}\times\overrightarrow{I_{21}A}\right)=\Omega\vec{k}\times\overrightarrow{I_{21}I_{02}}</math></center> | ||
El vector de posición relativo entre los dos centros instantáneos de rotación es | |||
<center><math>\overrightarrow{ | <center><math>\overrightarrow{I_{21}I_{02}}=\overrightarrow{OI_{02}}=h\vec{\jmath}_1 = \frac{a}{\mathrm{sen}^2(\theta)}\vec{\jmath}_1</math></center> | ||
y | y llegamos a la velocidad de traslación | ||
<center><math>\ | <center><math>\vec{v}^A_{01}=\Omega\vec{k}\times\left(\frac{a}{\mathrm{sen}^2(\theta)}\vec{\jmath}_1\right) = -\frac{a\Omega}{\mathrm{sen}^2(\theta)}\vec{\imath}_1</math></center> | ||
== | ===Mediante derivación=== | ||
La velocidad de traslación de la placa puede obtenerse también derivando respecto al tiempo la posición de cualquiera de sus puntos. Así, la posición instantánea de A la podemos escribir | |||
<center><math>\vec{ | <center><math>\vec{r}^A_{01}=\overrightarrow{OA}=x\vec{\imath}_1 + a\vec{\jmath}_1</math></center> | ||
y su velocidad de traslación será | |||
<center><math>\ | <center><math>\vec{v}^A_{01}= \left.\frac{\mathrm{d}\vec{r}^A_{01} }{\mathrm{d}t}\right|_1 = \dot{x}\vec{\imath}_1</math></center> | ||
El | El valor de la coordenada x lo obtenemos aplicando trigonometría, se trata del cateto contiguo de un triángulo rectángulo, de forma que | ||
<center><math>\ | <center><math>\frac{a}{x}=\mathrm{tg}(\theta)\,\,\,</math>{{tose}} <math>\,\,\,x = a\,\mathrm{cotg}(\theta)</math></center> | ||
y su derivada, por la regla de la cadena, vale | |||
<center><math>\ | <center><math>\dot{x}= -\frac{a\dot{\theta}}{\mathrm{sen}^2(\theta)}= -\frac{a\Omega}{\mathrm{sen}^2(\theta)}</math></center> | ||
lo que nos da la velocidad de traslación | |||
<center><math>\ | <center><math>\vec{v}^A_{01}=-\frac{a\Omega}{\mathrm{sen}^2(\theta)}\vec{\imath}_1</math></center> | ||
que coincide con lo que ya sabíamos. | |||
===Por composición de velocidades=== | |||
Alternativamente, supongamos que en el primer apartado no hemos sido capaces de localizar el centro instantáneo de rotación <math>I_{20}</math>, ni tampoco estamos seguros de si la posición de A se puede derivar o no. ¿Cómo podemos hallar en ese caso la velocidad de traslación? | |||
Recurrimos de nuevo a la fórmula de composición de velocidades | |||
<center><math>\vec{v}^ | <center><math>\vec{v}^A_{01}=\vec{v}^A_{02}+\vec{v}^A_{21}</math></center> | ||
Para la velocidad de A en el movimiento {21} tenemos que se trata de una rotación en torno al punto O, por lo que | |||
<center><math>\vec{v}^A_{21} = \omega_{21}\vec{k}\times\overrightarrow{OA}</math></center> | |||
La velocidad angular <math>\omega_{21}</math> ya la hemos indicado | |||
<center><math>\omega_{21}=\dot{\theta}=\Omega</math></center> | |||
El vector de posición lo podemos escribir tanto en el sistema “1” como en el “2” (considere un eje <math>OX_2</math> coincidente con la varilla) | |||
<center><math>\overrightarrow{OA}=L\vec{\imath}_2=x\vec{\imath}_1+a\vec{\jmath}_1</math></center> | |||
siendo | siendo | ||
<center><math>\ | <center><math>L = \frac{a}{\mathrm{sen}(\theta)}\,\,;</math>{{qquad}}{{qquad}}{{qquad}}<math>x=a\,\mathrm{cotg}(\theta)</math></center> | ||
Así obtenemos la velocidad | |||
<center><math>\vec{v}^A_{21}=\Omega L\vec{\jmath}_2 =\frac{a\Omega}{\mathrm{sen}(\theta)}\vec{\jmath}_2</math></center> | |||
Para el movimiento relativo {20} desconocemos la rapidez de A (si no sabemos dónde se halla el CIR), pero sí conocemos la dirección. El par cinemático asociado al contacto entre la placa y la barra exige que la velocidad sea puramente tangente a la barra, esto es | |||
<center><math>\vec{v}^A_{02}=v^A_{02} \vec{\imath}_2</math></center> | |||
Sumando las dos componentes obtenemos la velocidad | |||
<center><math>\vec{v}^A_{01}=v^A_{02}\vec{\imath}_2+\frac{a\Omega}{\mathrm{sen}(\theta)}\vec{\jmath}_2</math></center> | |||
Aunque esta velocidad posee dos componentes no nulas en la base “2”, debe tener una sola en la base “1”; ha de ser de la forma | |||
<center><math>\vec{v}^A_{01}=v^A_{01}\vec{\imath}_1</math></center> | |||
Tenemos ahora varias posibilidades de acción: | |||
* Sustituir los vectores de una base e igualar las componentes resultantes. | |||
* Proyectar sobre el vector <math>\vec{\jmath}_1</math> e imponer que el resultado sea nulo. | |||
* Proyectar sobre <math>\vec{\jmath}_2</math> para eliminar la cantidad <math>v^A_{02}</math> desconocida. | |||
Si elegimos este último camino, igualamos las dos expresiones para la velocidad de A | |||
<center><math>v\vec{\imath}_2+\frac{a\dot{\theta}}{\mathrm{sen}(\theta)}\vec{\jmath}_2=v^A_{01}\vec{\imath}_1</math></center> | |||
Multiplicando los dos miembros por el vector unitario <math>\vec{j}_2</math> nos queda | |||
<center><math>\frac{a\dot{\theta}}{\mathrm{sen}(\theta)} = v^A_{01} \vec{\imath}_1\cdot\vec{\jmath}_2</math></center> | |||
El último producto escalar vale | |||
<center><math>\vec{ | <center><math>\vec{\imath}_1\cdot\vec{\jmath}_2=\vec{\imath}_1\cdot\left(-\mathrm{sen}(\theta)\vec{\imath}_1+\cos(\theta)\vec{\jmath}_1\right)=-\mathrm{sen}(\theta)</math></center> | ||
y llegamos finalmente al resultado conocido | |||
<center><math>\ | <center><math>\frac{a\dot{\theta}}{\mathrm{sen}(\theta)} = -v^A_{01} \mathrm{sen}(\theta)</math>{{tose}}<math>\vec{v}^A_{01}=-\frac{a\dot{\theta}}{\mathrm{sen}^2(\theta)}\vec{\imath}_1</math></center> | ||
La | ==Determinación analítica del CIR== | ||
La posición del CIR <math>I_{20}</math> también puede hacerse analíticamente si, por cualquier método, somos capaces de determinar la velocidad de un punto en este movimiento y sabemos también la velocidad angular. | |||
Así para el punto O tenemos, despejando en la fórmula de composición de velocidades, | |||
<center><math>\vec{v}^O_{20}=\vec{v}^O_{21}-\vec{v}^O_{01}</math></center> | |||
La primera es la velocidad de rotación en torno al propio punto O (que será nula por tanto); la segunda es la de la traslación {01}, que será igual a la del punto A. Por tanto | |||
<center><math>\vec{v}^O_{20}=\overbrace{\vec{v}^O_{21}}^{=\vec{0}}-\overbrace{\vec{v}^O_{01}}^{=\vec{v}^A_{01}} = \frac{a\dot{\theta}}{\mathrm{sen}^2(\theta)}\vec{\imath}_1</math></center> | |||
La velocidad angular fue calculada previamente como | |||
<center><math>\ | <center><math>\omega_{20}=\omega_{21}-\omega_{10}=\dot{\theta}-0=\dot{\theta}</math></center> | ||
Hallamos ahora la posición relativa del CIR aplicando | |||
<center><math>\overrightarrow{ | <center><math>\overrightarrow{OI}= \frac{\vec{k}\times\vec{v}^O_{20}}{\omega_{20}}=\frac{a}{\mathrm{sen}^2(\theta)}\vec{k}\times\vec{\imath}_1 = \frac{a}{\mathrm{sen}^2(\theta)}\vec{\jmath}_1</math></center> | ||
que | que, por supuesto, coincide con lo obtenido de forma geométrica en el primer apartado. | ||
[[Categoría:Problemas de Movimiento Plano (GITI)]] | [[Categoría:Problemas de Movimiento Plano (GITI)]] | ||
Revisión del 13:57 16 ene 2024
Enunciado
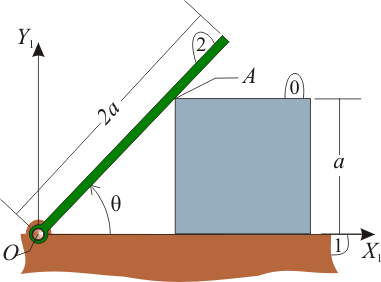
El esquema de la figura muestra una placa cuadrada de lado (sólido ``0"), uno de cuyos lados desliza sobre el eje horizontal fijo (sólido “1”), mientras que la placa permanece contenida siempre en el plano vertical fijo . Sobre el vértice A de dicha placa se apoya en todo instante una varilla delgada (sólido “2”), que gira con velocidad angular constante , alrededor de su extremo articulado en el punto fijo O (ver figura). Se pide:
- Determinar gráficamente la posición de los centros instantáneos de rotación , e .
- Calcular: i) La velocidad del vértice A de la placa en el movimiento de ésta respecto de los ejes fijos (movimiento {01}), expresada en función de la posición del sistema: . ii) La velocidad angular , correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {02}).
- Determinar analíticamente la posición del CIR del movimiento {02} (en función del ángulo ).
Centros instantáneos de rotación
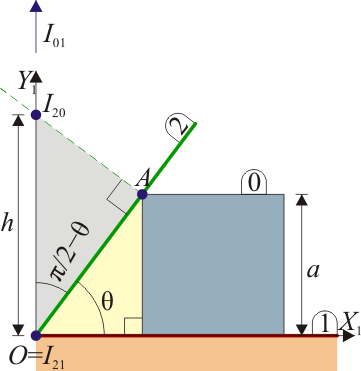
- Del movimiento {01}
- La placa realiza un movimiento de traslación horizontal, por lo que el centro instantáneo de rotación del movimiento {01} será un punto del infinito situado según la dirección vertical.
- Del movimiento {21}
- La barra efectúa un movimiento de rotación en torno al punto en el cual se encuentra articulada. Este punto será el CIR , que de hecho en este caso se trata de un centro permanente y no solo instantáneo.
- Del movimiento {20}
- Por el teorema de los tres centros, el CIR (coincidente con el CIR ) estará alineado con los otros dos. Puesto que está en el infinito según la dirección vertical, el CIR debe encontrarse en la vertical del punto , esto es, se trata de un punto del eje .
- Queda por determinar la posición sobre este eje. Para ello necesitamos la dirección de la velocidad de algún punto en el movimiento {20} o el {02}. El más simple es el punto A, donde contactan la barra y la placa. Este contacto impone un vínculo sobre las posibles velocidades de A. En particular, impide que A, en el movimiento {02}, tenga una componente perpendicular a la propia barra, ya que de ser así atravesaría ésta.
- Por tanto, es tangente a la propia barra. Ello implica que se encuentra en la intersección de la perpendicular a la barra por A con el eje .
- Podemos obtener las coordenadas de este punto empleando trigonometría. Si la altura de la placa es , la distancia OA es la hipotenusa de un triángulo rectángulo, por lo que
- La altura es la hipotenusa de otro triángulo rectángulo, uno de cuyos catetos es OA. Por ello
- En forma vectorial
Velocidades
Conociendo la posición del CIR {20}
Para hallar la velocidad de traslación de A (que es la misma de cualquier otro punto de la placa), podemos usar la ley de composición de velocidades
Cada una de estas velocidades es una rotación alrededor de su correspondiente CIR
La velocidad angular la da la derivada temporal del ángulo que forma el con el , que suponemos ligado a la propia barra:
donde se ha tenido en cuenta que, según el enunciado del ejercicio, .
La del movimiento {02} la obtenemos por composición de velocidades angulares, teniendo en cuenta que el movimiento {01} es una traslación
Resulta una velocidad angular igual y opuesta a la primera. De aquí llegamos a la velocidad de traslación
El vector de posición relativo entre los dos centros instantáneos de rotación es
y llegamos a la velocidad de traslación
Mediante derivación
La velocidad de traslación de la placa puede obtenerse también derivando respecto al tiempo la posición de cualquiera de sus puntos. Así, la posición instantánea de A la podemos escribir
y su velocidad de traslación será
El valor de la coordenada x lo obtenemos aplicando trigonometría, se trata del cateto contiguo de un triángulo rectángulo, de forma que
y su derivada, por la regla de la cadena, vale
lo que nos da la velocidad de traslación
que coincide con lo que ya sabíamos.
Por composición de velocidades
Alternativamente, supongamos que en el primer apartado no hemos sido capaces de localizar el centro instantáneo de rotación , ni tampoco estamos seguros de si la posición de A se puede derivar o no. ¿Cómo podemos hallar en ese caso la velocidad de traslación?
Recurrimos de nuevo a la fórmula de composición de velocidades
Para la velocidad de A en el movimiento {21} tenemos que se trata de una rotación en torno al punto O, por lo que
La velocidad angular ya la hemos indicado
El vector de posición lo podemos escribir tanto en el sistema “1” como en el “2” (considere un eje coincidente con la varilla)
siendo
Así obtenemos la velocidad
Para el movimiento relativo {20} desconocemos la rapidez de A (si no sabemos dónde se halla el CIR), pero sí conocemos la dirección. El par cinemático asociado al contacto entre la placa y la barra exige que la velocidad sea puramente tangente a la barra, esto es
Sumando las dos componentes obtenemos la velocidad
Aunque esta velocidad posee dos componentes no nulas en la base “2”, debe tener una sola en la base “1”; ha de ser de la forma
Tenemos ahora varias posibilidades de acción:
- Sustituir los vectores de una base e igualar las componentes resultantes.
- Proyectar sobre el vector e imponer que el resultado sea nulo.
- Proyectar sobre para eliminar la cantidad desconocida.
Si elegimos este último camino, igualamos las dos expresiones para la velocidad de A
Multiplicando los dos miembros por el vector unitario nos queda
El último producto escalar vale
y llegamos finalmente al resultado conocido
Determinación analítica del CIR
La posición del CIR también puede hacerse analíticamente si, por cualquier método, somos capaces de determinar la velocidad de un punto en este movimiento y sabemos también la velocidad angular.
Así para el punto O tenemos, despejando en la fórmula de composición de velocidades,
La primera es la velocidad de rotación en torno al propio punto O (que será nula por tanto); la segunda es la de la traslación {01}, que será igual a la del punto A. Por tanto
La velocidad angular fue calculada previamente como
Hallamos ahora la posición relativa del CIR aplicando
que, por supuesto, coincide con lo obtenido de forma geométrica en el primer apartado.





















































