Masas unidas por una cuerda con muelle
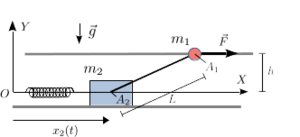
La masa de la figura está engarzada en un hilo horizontal sin rozamiento. La masa desliza sobre una superficie horizontal también lisa. La distancia entre las líneas horizontales es . Las dos masas están unidas por una cuerda ideal sin masa de longitud . La cuerda está siempre tensa. La gravedad actúa como se indica en la figura. La masa está a su vez unida a un muelle de longitud natural nula y constate elástica . El otro extremo del muelle está anclado en el punto . La masa está sometida a la acción de una fuerza horizontal .
- Dibuja el diagrama de fuerzas que actúa sobre cada partícula.
- Calcula el vector de posición de la partícula 1.
- En situación de equilibrio estático, encuentra la tensión de la cuerda y la fuerza que la superficie horizontal ejerce sobre la masa .
- Supongamos ahora que el contacto entre la masa y la superficie horizontal es rugoso con un coeficiente de rozamiento estático . Además, la masa se ajusta para que . ¿Qué condición debe cumplir para que el punto de coordenada sea un punto de equilibrio estático?











