Diferencia entre revisiones de «No Boletín - Suma y resta de dos vectores con módulos iguales (Ex.Sep/15)»
(Página creada con «==Enunciado== Sean <math>\,\vec{a}\,</math> y <math>\vec{b}\,\,</math> dos vectores libres no nulos y no paralelos (<math>\vec{a}\times\vec{b}\neq\vec{0}\,</math>), pero con módulos iguales (<math>|\vec{a}\,|=|\vec{b}\,|\,</math>). ¿Cuál de las siguientes relaciones existe con carácter general entre el vector diferencia <math>(\vec{a}-\vec{b}\,)\,</math> y el vector suma <math>(\vec{a}+\vec{b}\,)\,</math>? ('''NOTA''': sólo una de las cuatro opciones es correcta…») |
|||
| Línea 19: | Línea 19: | ||
Examinemos la opción (3). ¿Pueden tener igual longitud las dos diagonales de un rombo? Razonemos algebraicamente: | Examinemos la opción (3). ¿Pueden tener igual longitud las dos diagonales de un rombo? Razonemos algebraicamente: | ||
|\,\vec{a}\,-\,\vec{b}\,|=|\,\vec{a}\,+\,\vec{b}\,|\,\,\,\Rightarrow\,\,\,(\,\vec{a}\,-\,\vec{b}\,)\,\cdot\,(\,\vec{a}\,-\,\vec{b}\,)=(\,\vec{a}\,+\,\vec{b}\,)\,\cdot\,(\,\vec{a}\,+\,\vec{b}\,)\,\,\,\Rightarrow\,\,\,|\,\vec{a}\,|^2+\,|\,\vec{b}\,|^2-2\,\vec{a}\,\cdot\,\vec{b}=|\,\vec{a}\,|^2+\,|\,\vec{b}\,|^2+\,2\,\vec{a}\,\cdot\,\vec{b}\,\,\,\Rightarrow\,\,\,\vec{a}\,\cdot\,\vec{b}=0 | <math> | ||
</math> | |\,\vec{a}\,-\,\vec{b}\,|=|\,\vec{a}\,+\,\vec{b}\,|\,\,\,\Rightarrow\,\,\,(\,\vec{a}\,-\,\vec{b}\,)\,\cdot\,(\,\vec{a}\,-\,\vec{b}\,)=(\,\vec{a}\,+\,\vec{b}\,)\,\cdot\,(\,\vec{a}\,+\,\vec{b}\,)\,\,\,\Rightarrow</math> | ||
<math>\Rightarrow\,\,\,|\,\vec{a}\,|^2+\,|\,\vec{b}\,|^2-2\,\vec{a}\,\cdot\,\vec{b}=|\,\vec{a}\,|^2+\,|\,\vec{b}\,|^2+\,2\,\vec{a}\,\cdot\,\vec{b}\,\,\,\Rightarrow\,\,\,\vec{a}\,\cdot\,\vec{b}=0 | |||
</math> | |||
Se llega, pues, a la conclusión de que hay que descartar la relación (3) porque no se da con carácter general, sino sólamente en el caso particular de que los vectores <math>\,\vec{a}\,</math> y <math>\,\vec{b}\,</math> sean ortogonales, lo cual corresponde geométricamente a que el rombo sea en realidad un cuadrado. | Se llega, pues, a la conclusión de que hay que descartar la relación (3) porque no se da con carácter general, sino sólamente en el caso particular de que los vectores <math>\,\vec{a}\,</math> y <math>\,\vec{b}\,</math> sean ortogonales, lo cual corresponde geométricamente a que el rombo sea en realidad un cuadrado. | ||
Revisión actual - 13:33 9 ene 2024
Enunciado
Sean y dos vectores libres no nulos y no paralelos (), pero con módulos iguales (). ¿Cuál de las siguientes relaciones existe con carácter general entre el vector diferencia y el vector suma ?
(NOTA: sólo una de las cuatro opciones es correcta).
- (1)
- (2)
- (3)
- (4)
Solución
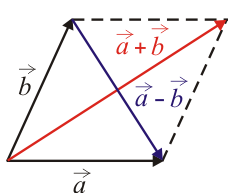
Obsérvese que las cuatro relaciones propuestas como posibles respuestas corresponden geométricamente a que los vectores suma y diferencia sean vectores opuestos, paralelos, de igual longitud o perpendiculares, respectivamente.
Al ser y vectores no nulos, no paralelos y con igual módulo, podemos considerarlos geométricamente representativos de los lados de un rombo, en cuyo caso los vectores suma y diferencia corresponden a las dos diagonales del citado rombo. Y es obvio que las dos diagonales de un rombo no pueden ser vectores opuestos ni paralelos en ningún caso. Por tanto, hay que descartar las opciones (1) y (2).
Examinemos la opción (3). ¿Pueden tener igual longitud las dos diagonales de un rombo? Razonemos algebraicamente:
Se llega, pues, a la conclusión de que hay que descartar la relación (3) porque no se da con carácter general, sino sólamente en el caso particular de que los vectores y sean ortogonales, lo cual corresponde geométricamente a que el rombo sea en realidad un cuadrado.
Finalmente, examinemos la opción (4). ¿Son perpendiculares las diagonales de un rombo? Razonemos algebraicamente:
Queda así comprobado que la perpendicularidad de los vectores suma y diferencia sólo exige la igualdad de módulos entre y (las diagonales de un rombo son, por tanto, perpendiculares). Así que la respuesta correcta a este ejercicio es la (4).













