Diferencia entre las páginas «No Boletín - Cuestión sobre reacción vincular de aro liso (Ex.Feb/14)» y «No Boletín - Ecuaciones horarias en coordenadas polares (Ex.Feb/14)»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
[[Archivo:polares.png|right]] | |||
El movimiento de una partícula <math>P\,</math>, de masa <math>m\,</math>, en el plano <math>OXY\,</math> queda descrito en coordenadas polares mediante las ecuaciones horarias: | |||
<center> | <center><math> | ||
[[ | \rho(t)=2R\,[1+\mathrm{cos}(\Omega t)]\,\,\,;\,\,\,\,\,\,\,\,\theta(t)=\Omega t | ||
</center> | </math></center> | ||
siendo <math>R\,</math> y <math>\Omega\,</math> constantes positivas conocidas. | |||
# Determine la velocidad y la aceleración de la partícula en componentes polares. | |||
# Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria. | |||
# Calcule la energía cinética de la partícula, y la potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula. | |||
# ¿Es el movimiento de la partícula un movimiento central con centro en el origen de coordenadas <math>O\,</math>? Razone la respuesta. | |||
==Velocidad y aceleración== | |||
La velocidad y la aceleración en componentes polares vienen dadas por las expresiones: | |||
<center><math> | |||
\vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta} | |||
\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{a}=\left(\ddot{\rho}-\rho\,\dot{\theta}^{2}\right)\, | |||
\vec{u}_{\rho}+\left(2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,\right)\,\vec{u}_{\theta} | |||
</math></center> | |||
Necesitamos, por tanto, calcular las derivadas de primer y segundo orden de <math>\rho\,</math> y <math>\theta\,</math> respecto al tiempo: | |||
<center><math> | |||
\dot{\rho}=-2R\,\Omega\,\mathrm{sen}(\Omega t)\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ddot{\rho}=-2R\,\Omega^2\,\mathrm{cos}(\Omega t)\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dot{\theta}=\Omega\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ddot{\theta}=0 | |||
</math></center> | |||
y sustituyendo en las expresiones de <math>\vec{v}\,</math> y <math>\vec{a}\,</math>, se obtiene: | |||
<center><math> | |||
\vec{v}=-2R\,\Omega\,\mathrm{sen}(\Omega t)\,\vec{u}_{\rho}\,+\, 2R\,\Omega\,[1+\,\mathrm{cos}(\Omega t)]\,\vec{u}_{\theta}\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, | |||
\vec{a}=-2R\,\Omega^2\,[1\,+\,2\,\mathrm{cos}(\Omega t)]\,\vec{u}_{\rho}-\, 4R\,\Omega^2\mathrm{sen}(\Omega t)\,\vec{u}_{\theta} | |||
</math></center> | |||
==Componentes intrínsecas de la aceleración y radio de curvatura== | |||
Podemos calcular la componente tangencial de la aceleración como la derivada respecto al tiempo de la celeridad: | |||
<center><math> | |||
v=|\vec{v}\,|=2\sqrt{2}\,R\,\Omega\,\sqrt{1+\mathrm{cos}(\Omega t)}\,\,\,\,\,\longrightarrow\,\,\,\,\,a_t=\displaystyle\frac{\mathrm{d}v}{\mathrm{d}t}=-\sqrt{2}\,R\,\Omega^2\,\displaystyle\frac{\mathrm{sen}(\Omega t)}{\sqrt{1+\mathrm{cos}(\Omega t)}} | |||
</math></center> | |||
Otra posibilidad sería calcular la componente tangencial de la aceleración proyectando el vector aceleración sobre la dirección del vector velocidad (que es tangente a la trayectoria): | |||
<center><math> | |||
a_t=\displaystyle\frac{\vec{v}\cdot\vec{a}}{v} | |||
</math></center> | |||
La componente normal de la aceleración podemos calcularla proyectando el vector aceleración sobre la dirección normal al vector | |||
velocidad: | |||
<center><math> | <center><math> | ||
\ | a_n=\displaystyle\frac{|\vec{v}\times\vec{a}|}{v}=3\,\sqrt{2}\,R\,\Omega^2\,\sqrt{1+\,\mathrm{cos}(\Omega t)} | ||
</math></center> | </math></center> | ||
El radio de curvatura se obtiene a partir de la componente normal de la aceleración y de la celeridad: | |||
<center><math> | <center><math> | ||
R_{\kappa}=\displaystyle\frac{v^2}{a_n}=\displaystyle\frac{4\,\sqrt{2}\,R}{3}\,\sqrt{1+\,\mathrm{cos}(\Omega t)} | |||
</math></center> | </math></center> | ||
==Energía cinética y potencia instantánea== | |||
<center> | A partir de la expresión de la celeridad, calculada anteriormente, se obtiene la energía cinética de la partícula: | ||
<center><math> | |||
< | K=\displaystyle\frac{1}{2}m v^2=4\, m R^2\,\Omega^2\,[1+\mathrm{cos}(\Omega t)] | ||
</math></center> | |||
La potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula puede calcularse como derivada temporal de la energía cinética: | |||
<center><math> | |||
P=\displaystyle\frac{dK}{dt}=-\,4\, m R^2\,\Omega^3\,\mathrm{sen}(\Omega t) | |||
</math></center> | |||
o bien puede calcularse también mediante el producto escalar de la fuerza neta por la velocidad: <math>\,P=\vec{F}\cdot\vec{v}=m\,\vec{a}\cdot\vec{v}\,</math> | |||
==¿Es un movimiento central con centro en el punto O?== | |||
La partícula tendría un movimiento central con centro en el origen de coordenadas <math>O\,</math> si la fuerza neta que actúa sobre ella fuese paralela al vector de posición (<math>\vec{F}=m\,\vec{a}\,\parallel\,\vec{r}=\rho\,\vec{u}_{\rho}\,</math>), es decir, si la componente acimutal de la aceleración fuese cero en todo instante de tiempo. Es evidente que en el presente ejercicio esto no se cumple, ya que dicha componente tiene el siguiente valor: | |||
<center><math> | |||
a_{\theta}=-\,4R\,\Omega^2\mathrm{sen}(\Omega t)\,\neq\,0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{no}\,\,\mathrm{es}\,\,\mathrm{movimiento}\,\,\mathrm{central}\,\,\mathrm{con}\,\,\mathrm{centro}\,\,\mathrm{en}\,\, O | |||
</math></center> | |||
Otra forma de comprobarlo es calculando la velocidad areolar respecto al punto <math>O\,</math>, la cual tendría que ser constante en el tiempo para que el movimiento fuese central con centro en <math>O\,</math>. En este caso no es constante: | |||
<center><math> | |||
V_{A}=\displaystyle\frac{1}{2}\,\rho^2\,\dot{\theta}=2\,R^2\,\Omega\,[1+\mathrm{cos}(\Omega t)]^2\,\neq\,\mathrm{cte}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{no}\,\,\mathrm{es}\,\,\mathrm{movimiento}\,\,\mathrm{central}\,\,\mathrm{con}\,\,\mathrm{centro}\,\,\mathrm{en}\,\, O | |||
</math></center> | |||
[[Categoría:Problemas de Dinámica del Punto (GITI)]] | [[Categoría:Problemas de Dinámica del Punto (GITI)]] | ||
Revisión actual - 18:59 10 ene 2024
Enunciado
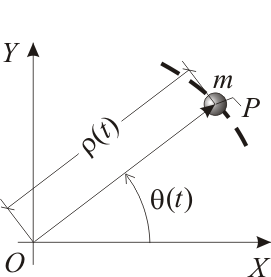
El movimiento de una partícula , de masa , en el plano queda descrito en coordenadas polares mediante las ecuaciones horarias:
siendo y constantes positivas conocidas.
- Determine la velocidad y la aceleración de la partícula en componentes polares.
- Halle las componentes intrínsecas de la aceleración de la partícula, y el radio de curvatura de su trayectoria.
- Calcule la energía cinética de la partícula, y la potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula.
- ¿Es el movimiento de la partícula un movimiento central con centro en el origen de coordenadas ? Razone la respuesta.
Velocidad y aceleración
La velocidad y la aceleración en componentes polares vienen dadas por las expresiones:
Necesitamos, por tanto, calcular las derivadas de primer y segundo orden de y respecto al tiempo:
y sustituyendo en las expresiones de y , se obtiene:
Componentes intrínsecas de la aceleración y radio de curvatura
Podemos calcular la componente tangencial de la aceleración como la derivada respecto al tiempo de la celeridad:
Otra posibilidad sería calcular la componente tangencial de la aceleración proyectando el vector aceleración sobre la dirección del vector velocidad (que es tangente a la trayectoria):
La componente normal de la aceleración podemos calcularla proyectando el vector aceleración sobre la dirección normal al vector velocidad:
El radio de curvatura se obtiene a partir de la componente normal de la aceleración y de la celeridad:
Energía cinética y potencia instantánea
A partir de la expresión de la celeridad, calculada anteriormente, se obtiene la energía cinética de la partícula:
La potencia instantánea desarrollada por la fuerza neta que actúa sobre la partícula puede calcularse como derivada temporal de la energía cinética:
o bien puede calcularse también mediante el producto escalar de la fuerza neta por la velocidad:
¿Es un movimiento central con centro en el punto O?
La partícula tendría un movimiento central con centro en el origen de coordenadas si la fuerza neta que actúa sobre ella fuese paralela al vector de posición (), es decir, si la componente acimutal de la aceleración fuese cero en todo instante de tiempo. Es evidente que en el presente ejercicio esto no se cumple, ya que dicha componente tiene el siguiente valor:
Otra forma de comprobarlo es calculando la velocidad areolar respecto al punto , la cual tendría que ser constante en el tiempo para que el movimiento fuese central con centro en . En este caso no es constante:



![{\displaystyle \rho (t)=2R\,[1+\mathrm {cos} (\Omega t)]\,\,\,;\,\,\,\,\,\,\,\,\theta (t)=\Omega t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de5b95bc71b9d6976632782aa047e3b0dc3354e4)









![{\displaystyle {\vec {v}}=-2R\,\Omega \,\mathrm {sen} (\Omega t)\,{\vec {u}}_{\rho }\,+\,2R\,\Omega \,[1+\,\mathrm {cos} (\Omega t)]\,{\vec {u}}_{\theta }\,\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\vec {a}}=-2R\,\Omega ^{2}\,[1\,+\,2\,\mathrm {cos} (\Omega t)]\,{\vec {u}}_{\rho }-\,4R\,\Omega ^{2}\mathrm {sen} (\Omega t)\,{\vec {u}}_{\theta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f333e396bb2d2f33e5e486e81543be1cf3d434)




![{\displaystyle K=\displaystyle {\frac {1}{2}}mv^{2}=4\,mR^{2}\,\Omega ^{2}\,[1+\mathrm {cos} (\Omega t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d049ccf460d16f10ce78e2dd4132cc154b3e02f7)




![{\displaystyle V_{A}=\displaystyle {\frac {1}{2}}\,\rho ^{2}\,{\dot {\theta }}=2\,R^{2}\,\Omega \,[1+\mathrm {cos} (\Omega t)]^{2}\,\neq \,\mathrm {cte} \,\,\,\,\,\Longrightarrow \,\,\,\,\,\mathrm {no} \,\,\mathrm {es} \,\,\mathrm {movimiento} \,\,\mathrm {central} \,\,\mathrm {con} \,\,\mathrm {centro} \,\,\mathrm {en} \,\,O}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e5b2247690eb1ee492ddcb20b77fd8a511666a3)